Принцип действия трансформаторов

Диапазон мощностей, в которых работают трансформаторы, огромен. Как уже было отмечено ранее, мощные силовые трансформаторы преобразуют мощности до 10⁹ вольт-ампер, тогда как трансформаторы маломощные (например, в источниках вторичного питания) преобразуют мощность в несколько вольт-ампер. Диапазон напряжений, в которых работают трансформаторы, также огромен: от нескольких вольт до сотен киловольт. Такая разнородность условий работы трансформаторов обуславливает большое разнообразие их конструкций, однако физическая суть их работы остается всегда одной и той же. На рис. 2.1 показана электромагнитная схема обобщенного трансформатора, которая является основой для анализа любых конструкций. На ферромагнитном сердечнике размещены две обмотки: первичная с количеством витков ω₁ и вторичная с количеством витков ω₂. Первичная обмотка подключается к источнику с напряжением U₁, ко вторичной обмотке присоединяется нагрузка. Токи, протекающие по обмоткам, создают помимо основного магнитного потока Ф_c поток рассеяния первичной обмотки Ф_σ1 и поток рассеяния вторичной обмотки Ф_σ2.

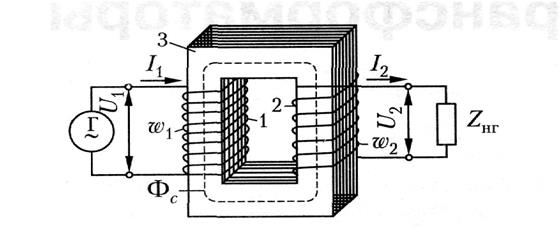
Рис. 2.1. Электромагнитная схема обобщенного трансформатора:

1 – первичная обмотка; 2 – вторичная обмотка;

3 – замкнутый ферромагнитный сердечник; Г – генератор;

Z_нг – сопротивление нагрузки

Рассмотрим электромагнитные процессы, возникающие в простейшем трансформаторе (рис. 2.1) при подключении первичной обмотки к сети переменного тока.

Физико-логическая схема этих процессов представлена на рис. 2.2.

Поясним эту схему, предварительно указав, что все величины, относящиеся к первичной обмотке, здесь отмечены подстрочным индексом «1», а относящиеся ко вторичной – индексом «2».

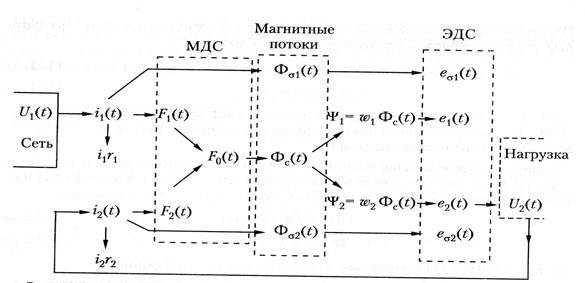
Рис. 2.2. Физико-логическая схема электромагнитных

процессов в трансформаторе

Из схемы видно, что возникающий под действием U₁(t) ток i₁(t) создает магнитодвижущую силу (МДС) F₁(t) = ω₁i₁(t), которая возбуждает в сердечнике магнитный поток взаимоиндукции Фс, магнитно связывающий первичную и вторичную обмотки трансформатора. Этот периодически изменяющийся поток индуцирует в обеих обмотках трансформатора электродвижущую силу (ЭДС) e₁(t) и e₂(t). В результате на зажимах вторичной обмотки возникает напряжение U₂(t), а если вторичная обмотка замкнута на сопротивление нагрузки, то и ток i₂(t). Протекая по вторичной обмотке, этот ток создает МДС F₂(t) = ω₂i₂(t). Следовательно, при включенной нагрузке (i₂(t) ≠ 0) поток в сердечнике Ф_с(t) будет возбуждаться под действием двух МДС F₁(t) и F₂(t). Результирующую этих МДС F₀(t) = F₁(t) + F₂(t) следует рассматривать как источник возбуждаемого в сердечнике магнитного потока Ф_с(t). Обратим внимание на то, что в изложенной концепции магнитной цепи, принятой в теории трансформаторов, предполагается, что поток взаимоиндукции Ф_с сцепляется со всеми витками первичной и вторичной обмотки. Магнитные потоки Ф_σ1(t) и Ф_σ2(t) принято называть потоками рассеяния, так как они не участвуют в передаче электромагнитной энергии из одной обмотки в другую. Они индуцируют ЭДС в своих обмотках, которые называются ЭДС рассеяния. Все выделенные МДС, магнитные потоки и индуцируемые ими ЭДС обведены на схеме пунктирной линией. Таким образом, математическая модель описания электромагнитных процессов в трансформаторе должна включать в себя соответствующие уравнения для электрических цепей (обмоток) и магнитной цепи (сердечника).

Электрические процессы в обмотках описываются уравнениями Кирхгофа, которые для рассматриваемого трансформатора имеют вид

U₁ + e₁ + e_σ1 = r₁ i₁, (2.1,а)

e₂ + e_σ2 = U₂ + r₂ i₂, (2.1,б)

где r₁ и r₂ – активные сопротивления первичной и вторичной обмоток соответственно; U₂ – напряжение на зажимах вторичной обмотки, то есть падение напряжения на сопротивлении нагрузки.

Уравнения, определяющие магнитные процессы в магнитопроводе трансформатора, также составляются на основе известных законов Ома и Кирхгофа для магнитных цепей, которые для мгновенных значений МДС и потоков имеют

F₁(t) + F₂(t) = F₀(t); (2.2, а)

Ф_c(t) = λ_μc F₀(t), (2.2, б)

где λ_μc – магнитная проводимость магнитопровода трансформатора. Выражения для ЭДС рассеяния – e_σ1 и e_σ2 – можно представить в виде

e_σ1 = - L_σ1 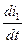; e_σ2 = - L_σ2 ,

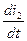где L_σ1 и L_σ2 – самоиндуктивности рассеяния первой и второй обмоток соответственно.

ЭДС e₁(t) и e₂(t) в соответствии со схемой, приведенной на рис. 2.2, определяются выражениями

e₁ = - ω₁ 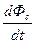; e₂ = - ω₂ ,

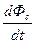Согласно схеме, приведенной на рис. 2.2, математическую модель двухобмоточного трансформатора можно представить системой уравнений для мгновенных значений напряжения и тока в дифференциальном виде:

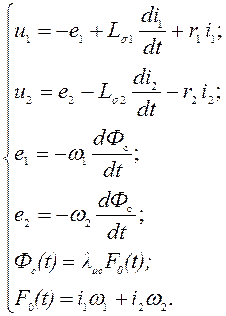(2.3)

Представленная модель может быть использована для анализа как установившихся, так и переходных режимов работы.