Равноугольная поперечно-цилиндрическая проекция Гаусса-Крюгера
Рассмотрим эту проекцию на шаре. Для этого введём систему сферических координат, как это показано на рис. 5.9.
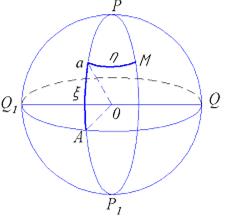
Рис.5.9
За начало координат принимается точка А, лежащая в пересечении экватора с меридианом P1AP, принимаемого за начальный в данной системе. Будем называть его осевым меридианом.
В новой системе координат за условный экватор принимается осевой меридиан, а за условные полюса точки Q и Q1 лежащие на экваторе и отстоящий от начала координат A на 90° по долготе. Положение точки M в этой системе координат определяется дугой осевого меридиана 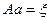 и дугой большого круга
и дугой большого круга 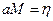 .
.
Зависимости между координатами 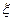 ,
, 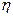 и координатами
и координатами 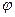 ,
, 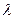 выражается формулами сферической тригонометрии.
выражается формулами сферической тригонометрии.
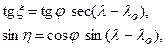 (5.25)
(5.25)
где 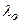 - долгота осевого меридиана.
- долгота осевого меридиана.
Возьмём теперь цилиндр, касательный к шару по осевому меридиану (рис.5.10) и перенесём на него условные меридианы Q1AA1A2Q, Q1aa1a2Q,, Q1bb1b2Q… и условные параллели - дуги малых кругов, параллельных плоскости меридиана – A1a1b1c1, A2a2b2c2 так как мы это делаем в нормальной равноугольной проекции Меркатора (см.5.4).
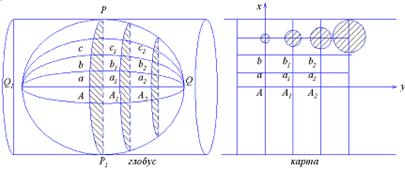
Рис.5.10
За ось x примем осевой меридиан 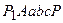 . За ось у - экватор Q,AQ (рис.5.10). Уравнения прямоугольных координат в этой проекции получим, если в выражениях (5.11) и (5.12) заменим
. За ось у - экватор Q,AQ (рис.5.10). Уравнения прямоугольных координат в этой проекции получим, если в выражениях (5.11) и (5.12) заменим 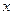 на
на 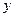 , а координаты
, а координаты 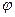 и
и 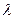 на
на 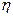 и
и 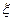 соответственно. В результате имеем
соответственно. В результате имеем
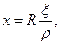
 (5.26)
(5.26)
Так как проекция равноугольная, увеличение по осям 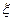 и
и 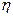 будет
будет
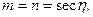 (5.27)
(5.27)
а эллипсы искажений - окружности радиусом 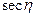 .
.
Из (5.27) следует, что искажение расстояний и площадей возрастает по мере удаления точки от осевого меридиана.
Чтобы эти искажения как-то ограничить, применение данной проекции ограниченно шестиградусными зонами. В каждой зоне имеется своя система прямоугольных координат 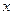 ,
, 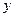 . При этом долгота осевого меридиана в каждой зоне определяет формула
. При этом долгота осевого меридиана в каждой зоне определяет формула
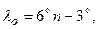
где n =1,2, 3,...60 - номер зоны.
В пределах зоны величина 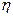 достаточно мала. Поэтому вместо сферической ординаты удобней использовать её линейное значение. Для этого разложим в (5.27)
достаточно мала. Поэтому вместо сферической ординаты удобней использовать её линейное значение. Для этого разложим в (5.27) 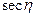 в ряд, ограничиваясь двумя членами
в ряд, ограничиваясь двумя членами
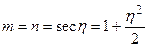 .
.
Заменив 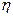 его линейным значением
его линейным значением 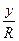 , получим известную формулу
, получим известную формулу
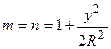 . (5.28)
. (5.28)
В Украине искажения длин линий на краю шестиградусной зоны достигает
в южной части 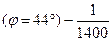 или 72 см на 1 км;
или 72 см на 1 км;
в северной части 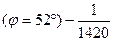 или 52 см на 1 км.
или 52 см на 1 км.
Искажение площадей соответственно
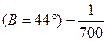 или 14 м2 на 1 га;
или 14 м2 на 1 га;
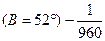 или 10 м2 на 1 га.
или 10 м2 на 1 га.
При составлении топографических планов в масштабе 1:5000 и крупнее такими искажениями пренебрегать нельзя. В этом случае применяют более узкие трёхградусные зоны, где долгота осевого меридиана вычисляется по формуле
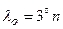 .
.
Как это видно на рис.5.10 линии сферических координат в проекции Гаусса-Крюгера — прямые линии.
При обратном переходе от сферических координат 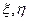 к географическим
к географическим 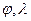 осевой меридиан и экватор изобразятся перпендикулярными прямыми (рис.5.11). Остальные меридианы - кривые линии, обращенные вогнутостью к осевому меридиану, а параллели - кривые, обращённые вогнутостью к ближайшему полюсу.
осевой меридиан и экватор изобразятся перпендикулярными прямыми (рис.5.11). Остальные меридианы - кривые линии, обращенные вогнутостью к осевому меридиану, а параллели - кривые, обращённые вогнутостью к ближайшему полюсу.
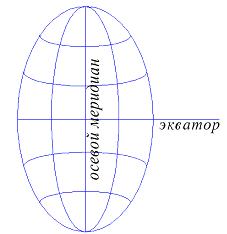
Рис.5.11
До сих пор мы рассматривали эту проекцию на шаре. При переходе к эллипсоиду вращения общий характер проекции существенно не меняется.
Прямоугольные координаты на эллипсоиде вычисляют по формулам (2.15), а искажение длин линий по формуле (2.18).
Дата добавления: 2022-05-27; просмотров: 260;











