Общая теория конических проекций
Как уже отмечалось в 4.2 в конической проекции меридианы - прямые, расходящиеся лучами из центра проекции в 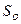 , а параллели -дуги концентрических окружностей с центром в точке
, а параллели -дуги концентрических окружностей с центром в точке 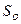 .
.
Уравнение конической проекции в общем виде представлено выражениями
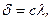 (4.8)
(4.8)
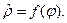 (4.9)
(4.9)
Таким образом при задании конкретного вида проекции необходимо установить значение коэффициента пропорциональности c и вид функции 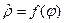 .
.
Для установления общих закономерностей конических проекций возьмём на глобусе и карте (рис.6.1) по два бесконечно близких
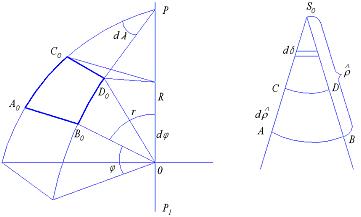
Рис.6.1
меридиана, составляющих между собой угол 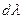 на глобусе и угол
на глобусе и угол 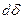 на карте, и по две бесконечно близкие параллели, отстоящие одна от другой на угол
на карте, и по две бесконечно близкие параллели, отстоящие одна от другой на угол 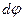 на глобусе и на отрезок -
на глобусе и на отрезок - 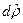 на карте. Знак минус взят потому, что с возрастанием широты
на карте. Знак минус взят потому, что с возрастанием широты 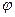 радиус
радиус 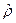 убывает.
убывает.
Частный масштаб по меридиану будет равен
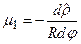 - для шара, (6.1)
- для шара, (6.1)
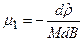 - для эллипсоида.
- для эллипсоида.
Увеличение масштаба m по меридиану для шара и эллипсоида будут соответственно равны
 (6.2)
(6.2)
где 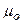 - масштаб глобуса и главный масштаб карты.
- масштаб глобуса и главный масштаб карты.
Для частного масштаба по параллелям можем записать
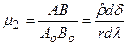 . (6.3)
. (6.3)
Продифференцируем (4.8) и подставим 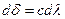 в (6.3). После очевидных преобразований получаем
в (6.3). После очевидных преобразований получаем
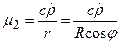 для шара, (6.4)
для шара, (6.4)
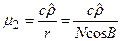 для эллипсоида.
для эллипсоида.
Соответственно увеличение по параллелям для шара и эллипсоида будет
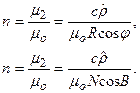 (6.5)
(6.5)
Так как в конической проекции меридианы и параллели перпендикулярны, то главные направления эллипса искажений совпадает с направлением меридиана и параллели.
Масштаб площадей определяется из выражения (3.20)
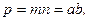
а направления наибольшего искажения углов из выражения (3.12)
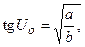
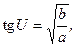
где 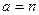 ,
, 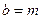 , если
, если 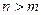 , или
, или 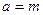 ,
, 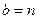 , если
, если 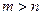 .
.
Опуская выводы, приведём готовые формулы для определения параметров проекции на широте, где увеличение по параллели наименьшее т.е. 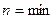 .
.
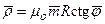 для шара, (6.6)
для шара, (6.6)
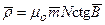 для эллипсоида,
для эллипсоида,
где черта над соответствующими обозначениями означает, что они соответствуют минимуму n.
На основании (6.5) можем записать
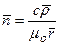 . (6.7)
. (6.7)
Подставим в (6.7) значение 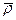 из (7.6) и принимая во внимание (6.4), найдём значение коэффициента пропорциональности c
из (7.6) и принимая во внимание (6.4), найдём значение коэффициента пропорциональности c
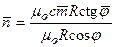 ,
,
откуда
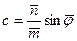 . (6.8)
. (6.8)
Таким образом, задавая широту 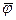 или
или 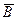 параллели, где мы хотим иметь наименьшее увеличение
параллели, где мы хотим иметь наименьшее увеличение 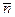 можно определить коэффициент пропорциональности c и параметры
можно определить коэффициент пропорциональности c и параметры 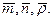
Дата добавления: 2022-05-27; просмотров: 179;











