Расчет на устойчивость статически неопределимых рам методом деформаций
Пример. Дана несвободная рама, имеющая одну степень свободы (рис.81,а). Уравнение устойчивости в данном случае принимает вид 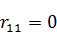 .
.
Выбираем основную систему (рис.81,б). Поворачиваем шайбу на единичный угол и строим соответствующую эпюру моментов.(рис.76).
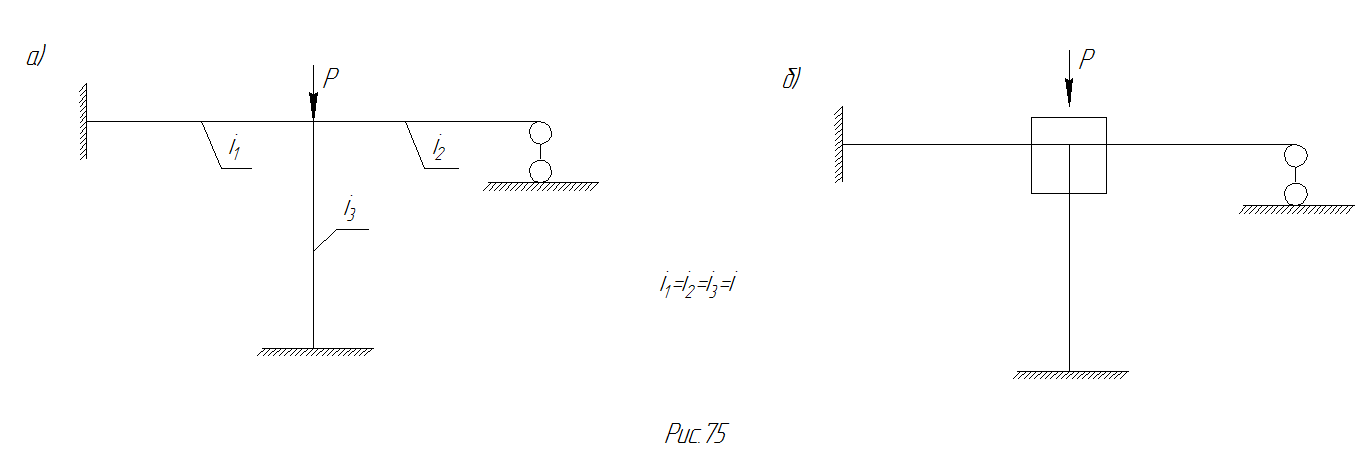
Рис. 81 Расчетная схема рамы и основная система
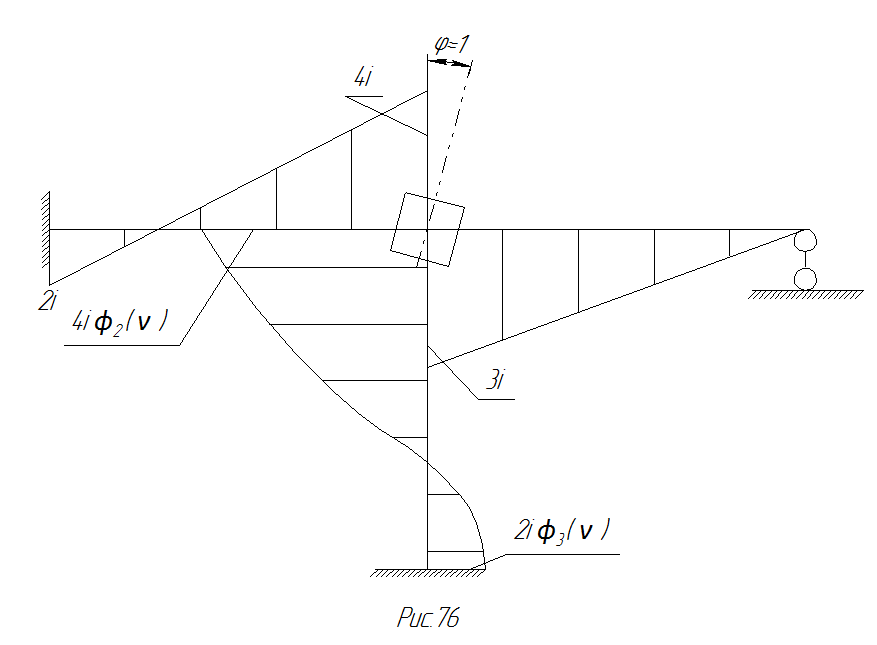
Рис. 82 Построение эпюры моментов с помощью типовых эпюр
Мысленно вырезаем шайбу (рис. 83) и из условия равновесия получаем:
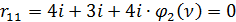 ,
,
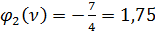 .
.
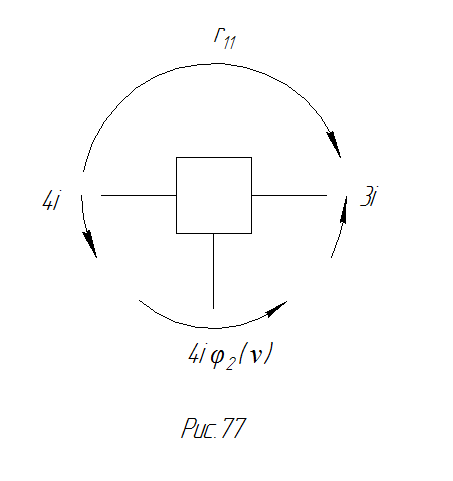
Рис. 83 Вырезаем узел и составляем уравнение равновесия
Из таблицы 1 находим, что 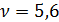 .
.
Тогда 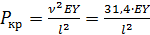
Пример. Дана несвободная рама, обладающая двумя степенями свободы, т.е. способная потерять устойчивость двумя различными путями (рис. 84, а).
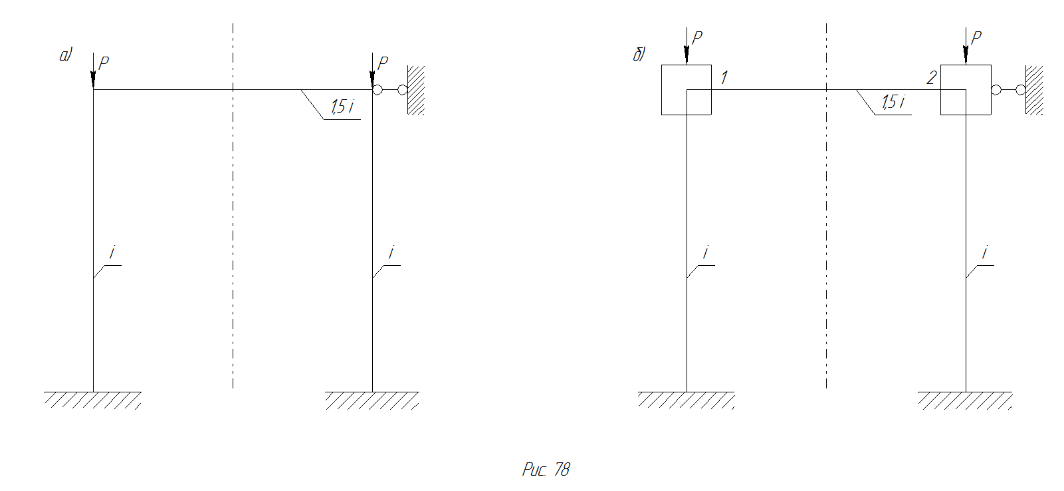
Рис. 84 Расчетная схема рамы и основная система рамы
Уравнение устойчивости для систем с двумя степенями свободы принимает вид:
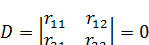
Так как 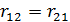 , то
, то 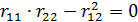 .
.
Выбираем основную систему (рис.84, б).
Поворачиваем на единичный угол шайбу № 1 и строим соответствующую эпюру моментов 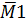 (рис. 83).
(рис. 83).
Эпюра 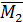 показана на рис. 84.
показана на рис. 84.
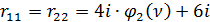
 .
.
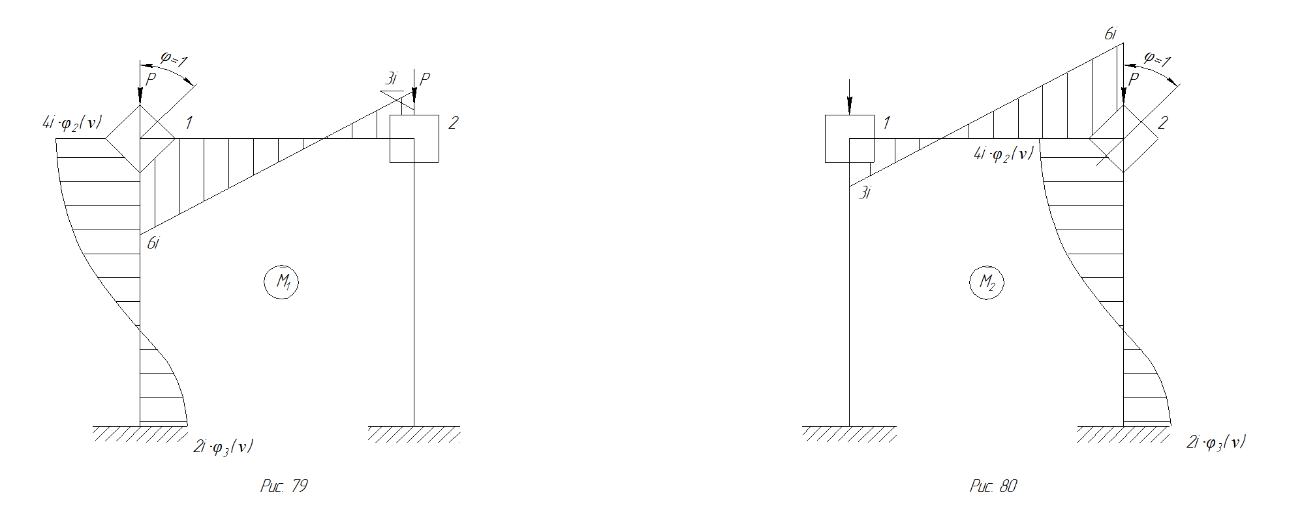
Рис. 83 Эпюра М1 Рис. 84 Эпюра М2
Уравнение устойчивости:
 ,
,
 ,
,
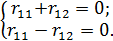
Производим подстановку коэффициентов в 1-е уравнение полученной системы:
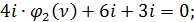
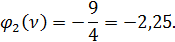
Из таблицы 1 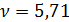
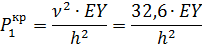
Подставляем коэффициенты во 2-е уравнение:
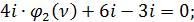
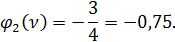
Из таблицы 1 находим 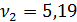
Тогда
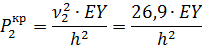
Каждому из двух значений критической силы соответствует своя форма потери устойчивости.
Если в системе уравнений
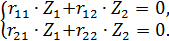
подставим значение коэффициентов, то из 1-го или 2-го уравнения системы получим, что 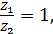
т.е. большей критической силе ( 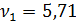 ) соответствует в данном случае обратно симметричная форма потери устойчивости (рис. 85)
) соответствует в данном случае обратно симметричная форма потери устойчивости (рис. 85)
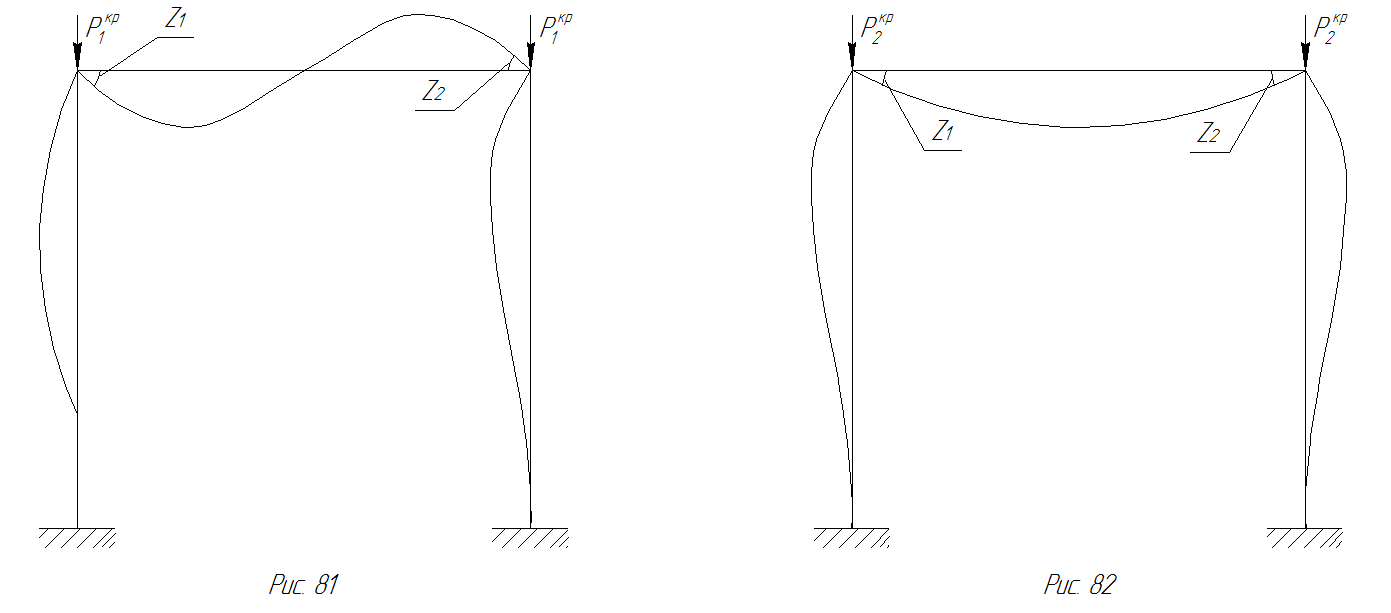
Рис. 85 Обратносимметричная Рис. 86 Прямосиммитричная
форма потери устойчивости рамы форма потери устойчивости рамы
Меньшей критической силе ( 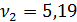 ) соответствует прямосимметричная норма потери устойчивости (рис. 86), так как из 1-го или 2-го уравнения получаем:
) соответствует прямосимметричная норма потери устойчивости (рис. 86), так как из 1-го или 2-го уравнения получаем:
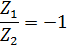
| <== предыдущая лекция | | | следующая лекция ==> |
| Динамический гаситель с учетом демпфирования | | | Лекция расчет на устойчивость пластин и оболочек |
Дата добавления: 2017-01-26; просмотров: 1656;











