Волоконно-оптические кабели

4.3.1 Основные положения. Световоды

Световоды – это однопроводные направляющие системы, относящиеся к классу диэлектрических волноводов, в которых создается граница раздела двух диэлектриков с различными значениями коэффициента преломления.

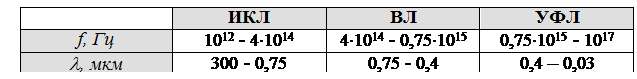Видный спектр света на шкале частоты, расположен между инфракрасными и ультрафиолетовыми диапазонами.

Для связи по световоду используют видимые лучи (0,4-0,75 мкм) и ближний диапазон ик лучей (0,85…1,3…1,55 до 4…6 мкм).

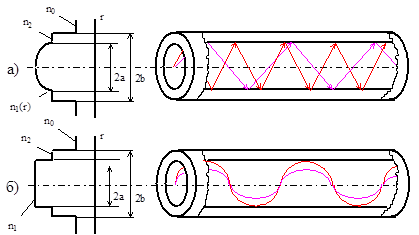Рис. 1 Световоды со ступенчатым (а) и градиентным (б) профилем показателя преломления.

Таким образом, световод имеет двухслойную конструкцию и состоит из сердцевины и оболочки с разными оптическими характеристиками (показателями преломления n₁ и n₂). Сердцевина служит для передачи электромагнитной энергии. Назначение оболочки - создание условий отражения на границе сердцевина-оболчка и защита энергии от излучения в окружающее пространство. Снаружи располагается защитное покрытие для предохранения волокна от механических воздействий и нанесения расцветки.

Наиболее широкое применение получили волоконные световоды двух типов:

1) ступенчатые.

2) градиентные.

У ступенчатых световодов показатель преломления в сердечнике постоянен и имеет резкий переход от n₁ сердцевины, к n₂ оболочки, и лучи зигзагообразно отражаются от границы сердечник-оболчка.

Градиентные световоды имеют непрерывное плавное изменение показателя преломления, в сердцевине по радиусу световода, от центра к периферии и лучи распространяются в световоде по волнообразным траекториям. Показатель преломления сердцевины меняется вдоль радиуса по закону показательной функции:

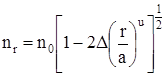
Где n₀ - показатель преломления в центре сердечника (при r = 0);

а - радиус сердечника;

u - показатель степени, описывающий профиль изменения показателя

преломления.

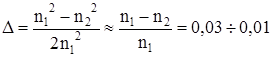
Чаще всего применяются волноводы с параболическим профилем u = 2.

Свет имеет двойственную природу:

1. Волновую 2. Корпускулярную (квантовую)

1. Волновая теория света обосновывает, что все свойства света совпадают со свойствами электромагнитных волн, т.е. свет является разновидностью электромагнитного поля. В этом случае применяется волновая теория электродинамики и уравнения Максвелла.

2. По корпускулярной теории свет - это поток быстро двигающихся мелких частиц корпускул (поток фотонов), которые излучаются светящимся телом. Здесь пригодна лучевая теория. Лучи света распространяются по законам геометрической оптики.

Сравнивая лучевую и волновую теории световодов, можно отметить, что лучевые методы менее громоздки и дают весьма наглядное объяснение физическим процессам, происходящих в волноводах.

4.3.2 Лучевая теория передачи по световодам.

Лучи света распространяются зигзагообразно по сердечнику волновода, многократно отражаясь от границы сердцевина-оболочка.

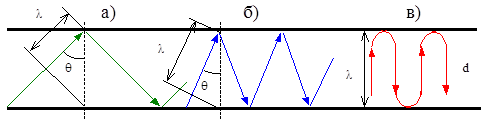Q®90° l®0 f®¥ Q®0° l®d f®f0 Q=0° l=d f=f0 Рис. 2 Распространение энергии в световоде: а) короткие волны (l®0); б) волны, соизмеримые с диаметром сердечника (l®d); в) критические волны

Здесь луч образует с поперечным сечением световода угол Q и многократно отражается от границы сердцевина-оболочка под углом 2Q. Установлено, что между длиной волны l, диаметром волновода d и углом Q, действует следующее соотношение: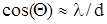

Рассмотрим предельные случаи распространения малых волн 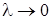и волн, соизмеримых с диаметром световода 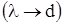, и критических длин волн. В первом случае ( 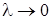и 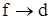) угол 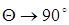, отражений мало и луч стремится к прямолинейному движению вдоль световода. Во втором случае ( 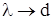и 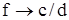) угол 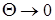, луч испытывает наибольшее количество отражений, и поступательное движение его весьма мало. При определенной длине волны наступает такой режим, когда 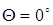и волна падает на оболочку световода и отражается перпендикулярно. В волноводе устанавливается режим стоячей волны, и энергия вдоль него не передается. Это свойственно случаю с критической длиной волны 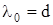и критической частоты .

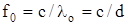Таким образом, в световоде могут распространяться лишь волны длиной, меньше чем диаметр сердечника световода ( ).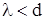

При 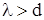требуется два провода (прямой и обратный), и передача происходит по обычной двухпроводной системе. При 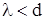не требуется такой системы, и передача происходит за счет многократного отражения волны от границ раздела двух сред с различными показателями преломления.

Однако в световоде, учитывая, что границей раздела сред сердечник-оболочка является прозрачное стекло, возможно, не только отражение оптического луча, но и проникновение его в оболочку. Для предотвращения перехода энергии в оболочку и излучения в окружающее пространство необходимо соблюдать условие полного внутреннего отражения. Реализация этого условия показана на рис. 3

Рис. 3 Условие полного внутреннего отражения

Угол полного внутреннего отражения определяется из следующего соотношения:

Закон преломления:

,

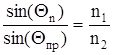необходимо чтобы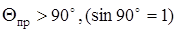

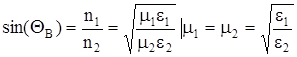
Где n₁ и n₂ - коэффициенты преломления оболочки и сердечника соответственно;

m ₁, m ₂ и e ₁, e ₂ - относительные магнитные и диэлектрические проницаемости.

При угле 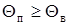энергия, поступившая в сердечник полностью отразится и зигзагообразно распространится по световоду.

При угле, меньшем угла полного отражения, т.е. 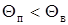, энергия проникает в оболочку, излучается в окружающее пространство, и передача по световоду не эффективна, т.к. имеется преломленный луч. Режим полного внутреннего отражения предопределяет условие подачи света на входной торец волоконного световода. Как видно из рис.3 световод пропускает лишь свет , заключенный в пределах телесного угла Q₀, величина которого обусловлена углом полного внутреннего отражения Q_В. Этот телесный угол характеризуется апертурой­.

Апертура - это угол между оптической осью и одной из образующих светового конуса, попадающего в торец волнового световода, при котором выполняется условие полного внутреннего отражения. Обычно пользуются понятием числовой апертуры:

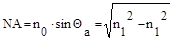
Где n₀, n₁, n₂ - показатели преломления воздуха, сердечника, оболочки. Имея в виду, что для воздуха n₀=1, получим:

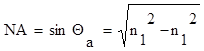
Апертура определяется из условия полного внутреннего отражения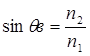

По закону синуса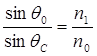

Апертура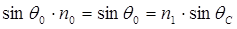

Известно, что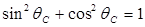

Тогда:

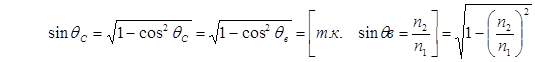
Откуда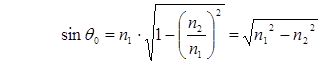

По световодам возможна передача лучей двух видов: меридиальных и косых. Меридиальные расположены в плоскости, проходящей через ось световода. Косые лучи не лежат в плоскости световода, они имеют сложные траектории прохождения в световоде.

Как видно из Рис.3, между углом полного внутреннего отражения Q_В и апертурным углом падения луча Q_А имеется взаимосвязь. Чем больше угол Q_В, тем меньше апертура волокна Q_А.

Рассмотрим критические частоты и длины волн волоконных световодов. Выше было показано, что между длиной волны l и диаметром сердцевины световода d имеется соотношение 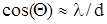. Учитывая, что 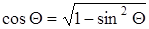, и используя условие полного отражения 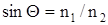, получим 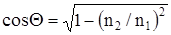. Приравнивая правые части выражений по синусам, имеем:

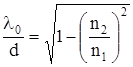
Откуда критическая длина волны волоконного световода:

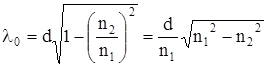
Критическая частота: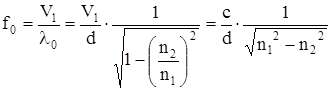

Где V₁ - скорость распространения волны в сердечнике.

Анализируя полученные соотношения, можно отметить – чем больше диаметр сердцевины d и чем сильнее отличаются n₁ и n₂, тем больше критическая длина волны и соответственно ниже критическая частота.

Выше изложенное дает основание сделать вывод, что при частотах выше критической f₀, вся энергия поля концентрируется внутри сердечника световода и эффективно распространяется вдоль него. Ниже критической частоты энергия рассеивается в окружающем пространстве и не передается по световоду.

4.3.3 Волновая теория передачи по световодам.

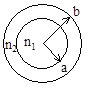Рис. 4К расчёту световода.

Рассмотрим волоконный световод без потерь двухслойной конструкции. Поперечные составляющие напряжённости электрического и магнитного полей могут быть выражены через продольные составляющие E_z и H_z.

Используем цилиндрическую систему координат, ось которой совместима с осью цилиндра. Для сердечника имеем следующую систему уравнений ( ):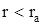

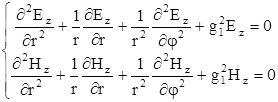
Где 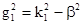- поперечный коэффициент распространения в сердечнике

световода;

b - коэффициент распространения в световоде;

k₁ - волновое число среды с коэффициентом преломления n₁:

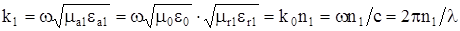
Решение данных уравнений для сердечника следует выразить через цилиндрические функции первого рода функций Бесселя, имеющие конечные значения при r = 0.

Поэтому для r < a можно записать:

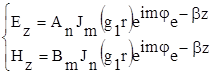, где A_n и B_n - постоянные интегрирования.

Для оболочки имеем аналогичную систему уравнений:

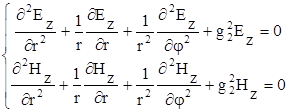
Где 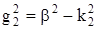- поперечный коэффициент распространения в оболочке световода;

b - коэффициент распространения в световоде;

k₂ - волновое число среды с коэффициентом преломления n₂:

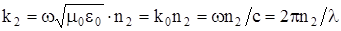
Для решения данных уравнений, исходя из условия, что при r ® ¥ поле должно стремиться к нулю, следует при r > a использовать функции Ганкеля:

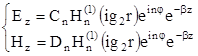где C_n и D_n - постоянные интегрирования.

Тогда для поперечных составляющих поля в оболочке можно написать:

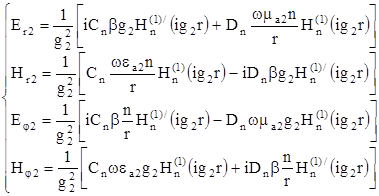
Постоянные интегрирования A_n, B_n, C_n, D_n могут , быть определены из на основании граничных условий. Используем условие равенства тангенциальных составляющих напряжённостей электрических и магнитных полей на поверхности раздела сердцевина- оболочка (при r = a):

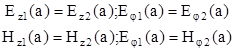
Найдя постоянные интегрирования и подставив их в уравнения, после соответствующих преобразований получим следующее трансцендентное уравнение:

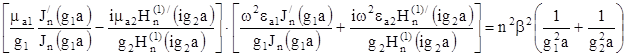
В приведенных формулах индексом n нумеруется порядок функции, а m - номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя.

Обычно режим работы световода характеризуется параметром V, включающим радиус сердечника, длину волны и коэффициенты преломления сердечника и оболочки. Этот параметр называется нормированной (характеристической) частотой. Он определяется как сумма аргументов функции Бесселя – 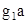и Ганкеля – :

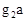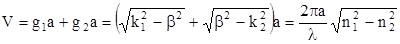
Рассмотрим критические частоты и длины волн световодов. В волоконных световодах при очень высоких частотах почти вся энергия поля концентрируется внутри сердцевины световода, с уменьшением частоты происходит перераспределение поля, и оно переходит в окружающее пространство. При определенной частоте f₀- критической, или частоте отсечки, поле больше не распространяется вдоль световода и вся энергия рассеивается в окружающем пространстве.

Воспользуемся ранее приведенными соотношениями

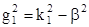(при r < a); 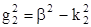(при r > a).

Получим: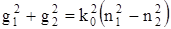

Для определения критической частоты f₀ надо принять g₂ = 0 (при всех значениях g₂ > 0 поле концентрируется в сердцевине световода, а при g₂ = 0 оно выходит из сердцевины и процесс распространения по световоду прекращается). Условие g₂ = 0 соответствует по закону геометрической оптике углу полного внутреннего отражения, при котором отсутствует преломленная волна, а есть только падающая и отраженная волны. В данном случае имеем 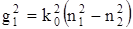. Подставив сюда значения 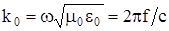, определим критическую частоту f₀ световода:

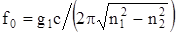
Умножим числитель и знаменатель на параметр а (радиус сердечника), тогда

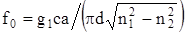
Соответственно критическая длина волны, передаваемая по световоду,

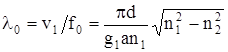, где g₁a = p_nm

Сравнивая эту формулу с ранее полученной методом геометрической оптики, видим полную тождественность. Отметим, что разница лишь в параметре 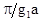, характеризующим тип волны.

Для определения критических частот различных типов волн рассмотрим корни ранее полученного выражения бесселевых функций 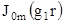для симметричных и 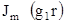- несимметричных волн. Эти равенства дают бесконечное число корней, значения которых приведены в табл. 4.3.1.

Корни бесселевых функций (g₁a = P_nm) могут быть представлены в следующем виде. При частоте отсечки 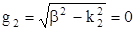, поэтому имеем равенство .

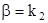Тогда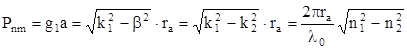

Сравнивая полученную формулу с формулой нормированной частоты видим, что они идентичны (p_nm=V), и отличие состоит лишь в том, что вместо общей величины l, взят ее частный случай l₀.

Таким образом, каждая мода имеет нормированную частоту, которая определяет область ее существования.

При V < V₀ имеем f < f₀, т.е. частота меньше критической и волна по сердцевине волокна не распространяется, т.е. не существует. Область существования волны, имеющей нормированную частоту отсечки V > V₀, составляет f > f₀.

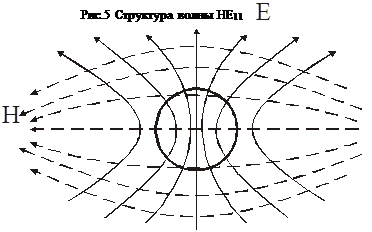
В световоде распространяется лишь один тип волны НЕ₁₁, когда соблюдается условие 0 < V < 2.405. При выборе частоты передачи или толщины сердечника световода исходят из этого условия. Выбирая параметры световода таким образом, чтобы не могли распространяться высшие моды, можно получить режим передачи только одной моды HE₁₁.

Такая ситуация реализуется при условии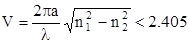

Это условие можно выполнить, уменьшая либо разность показателей преломления, либо радиус сердечника. Для типичного случая (n₁ = 1.5 и n₂ = 1.49) U»0.6a / l и, следовательно, максимальное значение диаметра сердечника (2a) составит 6,8 мкм при l = 0,85 мкм и 12,8 мкм при l=1,6мкм. Волна НЕ₁₁ используется при передачи по одномодовым световодам.

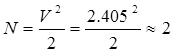
В одномодовом режиме число мод получается равным 2. Это объясняется тем, что мода волны НЕ₁₁ по сути это выражение двух мод в одну, имеющих для круглой сердцевины одинаковые параметры распространения. В случае некруглости сердцевины оптического волокна, каждая из составляющей моды HE₁₁ имеет свои значения параметра распространения, что приводит к различным значениям скорости распространения.

Для многомодового оптического волокна диаметр сердцевины, как правило, составляет 50 мкм, а диаметр оболочки 125 мкм.

Достоинства: одномодовых систем являются весьма широкий диапазон частот и большая пропускная способность, так как с увеличением числа мод полоса передаваемых частот снижается. Используются на междугородних линиях.

Недостатки: однако, одномодовые системы из-за малого диаметра сердечника волокна менее надежны и имеют большие потери на вводе в световод, поэтому они используются в основном на междугородних ВОЛС, обеспечивая большую дальность связи и высокую пропускную способность.

Общее число передаваемых мод в световодах может быть определено по формулам:

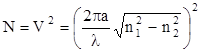- для ступенчатого профиля,

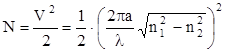- для градиентного профиля.

4.3.4 Затухание световодов

Волоконные световоды характеризуются двумя важнейшими параметрами: затуханием и дисперсией. Затухание предопределяет длину регенерационных участков (расстояние между регенераторами). Дисперсия приводит к ограничению полосы передачи по световоду и уменьшению длины регенерационного участка. Коэффициент затухания световодных трактов оптических кабелей a обусловлен собственными потерями в волоконных световодах a_C и дополнительными потерями, так называемыми кабельными a_K, вызванными скруткой, а также деформацией и изгибами световодов при наложении покрытий и защитных оболочек в процессе изготовления оптического кабеля: a = a_C + a_K.

Собственные потери волоконных световодов состоят в первую очередь из потерь поглощения энергии в диэлектрике a_П и потерь рассеяния ее на мельчайших частицах световодной структуры a_Р. Потери поглощения существенно зависят от чистоты материала и при наличии посторонних примесей могут достигать значительной величины (a_П + a_ПР). Потери на рассеяние лимитируют предел минимально допустимых значений потерь в волоконных световодах. В результате:

a = a_П + a_Р + a_ПР + a_К.

Затухания поглощения a_П связано с потерями на диэлектрическую поляризацию, линейно растет с частотой и существенно зависит от свойств материала световода (tgd).

Затухание поглощения определяется отношением величины потерь в световоде к удвоенному значению всей мощности, передаваемой по световоду:

a= P_П / 2P, где P_П = GU²; P = U²/Z_B,

Тогда a_П = 0.5GZ_B, где:

G = we_A tgd - проводимость материала световода;

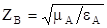- волновое сопротивление;

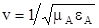- скорость распространения энергии по световоду.

Используя условие v = c/n и c = lf, получаем формулу расчета потерь на поглощение, Дб/км: ,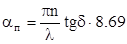

Где 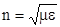- показатель преломления;

l - длина волны;

tgd - тангенс угла диэлектрических потерь в световоде.

Выражая tgd через комплексный показатель преломления, получаем:

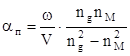
Если коэффициент преломления имеет действительное значение n = n_Д, то tgd = 0 и потери на поглощение отсутствуют.

Потери на рассеяние (a_Р) обусловлено неоднородностями материала волоконного световода, размеры которых меньше длины волны, и тепловой флуктуацией показателя преломления.

Рассеяние, называемое рэлеевским, определяются по формуле, дБ/км:

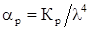
где К_Р - коэффициент рассеяния, равный 0,8 мкм⁴* (дБ/км) – для кварца.

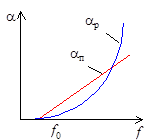Рис. 5 Частотная зависимость затухания поглощения aп и затухания рассеяния aр

Волнообразный характер потерь на примере (a_ПР) обусловлен проявлением резонансных всплесков затухания при определенной длине волны. Из таблицы видна целесообразность работы световода при l равной 1,3 и 1,55 мкм.

Кроме собственных потерь (a_С) надлежит учитывать также дополнительные- кабельные потери (a_К), связанные с геометрией волокна и наличием оболочки (a=a_С+a_К).

Основными факторами, приводящими к потерям, вызываемыми геометрией волокна, являются:

1. Непостоянство размеров поперечного сечения сердцевины волокна по длине

2. Неровности границы раздела сердцевина - оболочка

3. Нерегулярности, связанные с наличием микроизгибов и макроизгибов волокна.

Макроизгибы обусловлены скруткой волоконных световодов по геликоиде вдоль всего оптического кабеля. Микроизгибы связаны с конструктивными и технологическими неоднородностями волоконного световода в процессе его изготовления (рис.6). Дополнительное затухание за счет потерь на излучение при макро изгибах дБ:

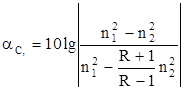
где R=R_ИЗ/2a;

R_ИЗ - радиус изгиба;

а - радиус сердцевины волокна;

n₁ и n₂ - показатели преломления сердцевины и оболочки волокна.

Дополнительное затухание за счет излучения при микро изгибах, дБ:

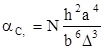
где h – высота (радиус) микро изгиба; a – радиус сердцевины волокна; b – диаметр волокна; N – число микро изгибов.

При достаточно хорошо отработанной технологии производства оптических кабелей доминируют потери на микро изгибы. Наличие оболочки и защитного покрытия волокна также приводит к дополнительным потерям за счет частичного проникновения поля в эти среды.

Установлено, что все эти кабельные потери a_K приводят к значительному увеличению затухания. Так, если собственное затухание световода a_C=3дБ/км, то за счет дополнительных кабельных потерь оно возрастает до 4...5 дБ/км.

У определённого вещества можно наблюдать окна прозрачности. Это участки зависимости затухания от длины волны, имеющие минимальные значения. Для очищенного кварцевого стекла один из таких участков лежит в пределах 1,3...1,55 мкм. Этим объясняется целесообразность применения волн этой длины для организации междугородней связи с расстоянием между регенераторами 40...80 км.

4.3.5 Дисперсия

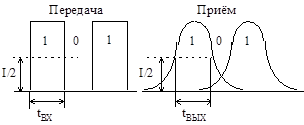Рис. 7 Уширение импульсов за счёт дисперсии

Дисперсия определяет полосу частот, пропускаемую световодом и соответственно объем информации, который можно передавать по оптическим кабелям. В идеализированном варианте по световоду возможна организация огромного числа каналов на большие расстояния, а фактически имеются значительные ограничения. Это обусловлено тем, что сигнал на входе приемного устройства приходит разжатым и искаженным, и чем длинней линия, тем больше искажается передаваемый сигнал. Данное явление носит название дисперсии, и обусловлено оно различным временем распространения различных мод в световоде и наличием частотной зависимости показателя преломления.

Дисперсия t – это рассеяние во времени спектральных или модовых составляющих оптического сигнала, приводящее к «уширению» импульса на приеме. Величина уширения определяется как квадратичная разность длительности импульсов на выходе и входе кабеля, по формуле:

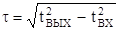
Причем значения t_ВЫХ и t_ВХ берутся на уровне половины амплитуды импульсов.

Связь между дисперсией и полосой частот, передаваемых по волоконному световоду. Приближенно выражается соотношением: DF = 1/t. Так, если t = 20нс/км, то DF = 50 МГц×км.

Дисперсия не только ограничивает частотный диапазон использования световодов. Она существенно снижает дальность передачи по оптическому кабелю, так как чем длиннее линия, тем больше проявляется дисперсия и больше уширение импульса.

Пропускная способность оптического кабеля существенно зависит от типа и свойств волоконных световодов (одномодовые, многомодовые, градиентные), а также от типа излучателя (лазера, световода).

Дисперсия складывается из трех составляющих:

1) межмодовый t_мод

2) материальной t_мат

3) волноводной t_вв

Рассмотрим поподробнее:

1) Модовая дисперсия обусловлена наличием большого числа мод, время распространения которых различно. В геометрической интерплитации соответствующие модам лучи идут под различными углами, проходят различный путь в сердцевине волокна и, следовательно, поступают на вход с различной задержкой.

В ступенчатых волноводах при многомодовой передаче доминирует модовая дисперсия, достигающая больших значений (20–250 нс/км), из-за разного времени прохождения лучей.

В одномодовых, ступенчатых световодах отсутствует модовая дисперсия. Здесь проявляется волноводная и материальная дисперсии, но они почти равны по абсолютной величине и противоположны по фазе в широком спектре. В силу этого происходит их взаимная компенсация и результирующая дисперсия при l = 1,2…1,7 мкм не больше 1 нс/км.

В градиентных световодах происходит выравнивание времени распространения различных мод и определяющей является дисперсия материала, которая уменьшается с увеличением длины волны. По абсолютной величине она колеблется в пределах 3...5 нс/км.

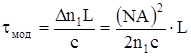- для ступенчатых световодов

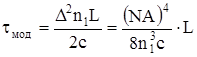- для градиентных световодов

Где 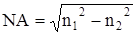- числовая апертура

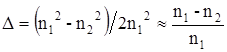
L - длина волновода

с - скорость света

2) Материальная дисперсия - обусловлена зависимостью показателя преломления от длины волны.

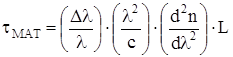
Где Dl - ширина спектральной линии источника излучения, равная 1-3 мм для лазера, и 20-40 мм для светоизлучающего диода.

Для расчетов также можно пользоваться упрощенной формулой и экспериментальными данными:

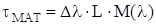
Где М(l) - удельная материальная дисперсия

3) Волноводная дисперсия характеризуется зависимостью коэффициента распространения моды от длины волны.

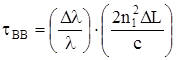
Где 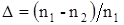, тогда упрощенная формула:

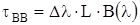
Где М(l) - удельная волноводная дисперсия

Результирующие значения уширения импульсов за счет модовой (t_МОД), материальной (t_МАТ) и волноводной (t_ВВ) дисперсии определяются формулой:

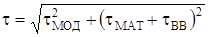
С учетом реального соотношения вкладов отдельных видов дисперсии имеем для многомодовых волокон t=t_МОД, а для одномодовых t=t_МАТ+t_ВВ.

Частотная полоса пропускания существующих конструкций оптических кабелей колеблется в широких пределах и составляет 30 до 1000 МГц×км. Она неодинакова для различных типов световодов. Для градиентных световодов с лазерным источником света частотная полоса составляет 100...250 МГц×км. В многомодовых световодах она сужается до 50 МГц×км. Наивысшей пропускной способностью обладают одномодовые световоды. У них полоса пропускания достигает 0,5...1 ГГц×км.

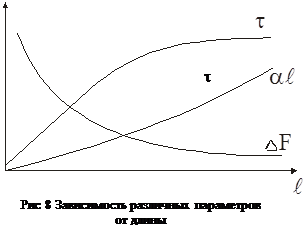
Явление дисперсии приводит как к ограничению пропускной способности (DF) оптических кабелей, так и к снижению дальности передачи по ним. Эти параметры - полоса частот DF и дальность передачи l взаимосвязаны. Соотношение между ними для коротких линий выражается формулой:

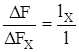Где значения с индексом х - искомые, без индекса - заданные.

Соответственно:

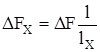или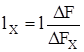

В длинных линиях (примерно свыше 8 км), в которых процесс распространения волны уже установился, действует квадратичный закон соотношения между l и DF, т.е.

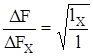тогда: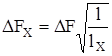

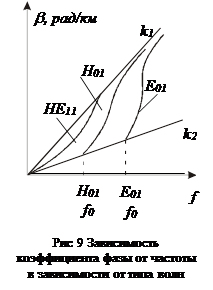
l

Длина регенерационного участка выбирается по наименьшему значению l_a или l_DF, т. е. таким образом, чтобы не превышать допустимые значения по затуханию тракта (а_доп = a×l) и пропускной способности (DF_доп).

4.3.6 Коэффициент фазы, волновое сопротивление и

скорость передачи по световодам

Коэффициент фазы (распространения) b является важнейшим параметром, определяющим форму сигнала, качество и скорость передачи по линии.[рад/км].

,

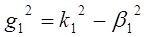где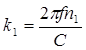

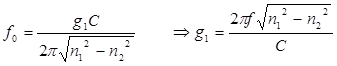
тогда

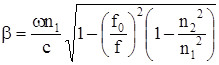
f – расчетная частота

– критическая частота

c – скорость света,

d – диаметр сердцевины,

P_nm – значение корней функции Бесселя для различных типов волн.

Фазовая скорость распространения волны

Скорость (км/с) перемещения вдоль линии фронта волн называется фазовой скоростью распространения волны:

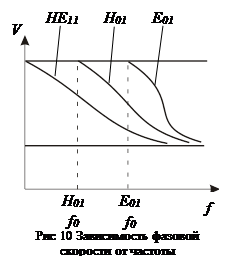
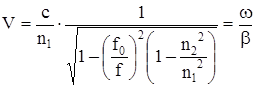
В предельных случаях, при f₀ и f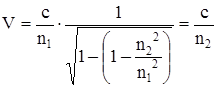_¥: при f = f₀, и

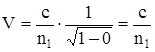при f ® ¥

c/n2

c/n1

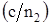Фазовая скорость передачи по световоду при критической частоте равна скорости распространения волны в оболочке , а с ростом частоты, поле все больше концентрируется в сердцевине световода, происходит эффективная передача и скорость определяется свойствами сердцевины .

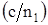Используя значение критической частоты f₀ ,формула для расчета фазовой скорости запишется: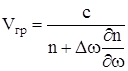

4.3.8 Взаимные переходные помехи в оптических кабелях

Волоконные световоды, находящиеся в общем, сердечнике кабеля, оказывают мешающее воздействие на соседние световоды в виде помех. Природа взаимных переходных помех в оптических кабелях связана с характеристикой волн, действующих в волоконных световодах. Рассмотрим эти волны.

В общем случае в волоконном световоде могут существовать три типа волн: направленные, вытекающие и излучаемые. Действие и преобладание какого-либо типа волн связано, с первую очередь с апертурой и соотношением углов падения волны Q_n и полного внутреннего отражения.

Направляемые волны (волны сердечника) – основной тип волны, распространяющийся по световоду. Вся энергия сосредоточена внутри сердечника световода и обеспечивает передачу информации. Направляемые волны возбуждаются при вводе лучей в торец под углом меньшим телесного угла апертуры, что обеспечивает Q_n > Q_в.

Излучаемые (пространственные) волны возникают при вводе лучей под углом больше угла апертуры Q_a, такой угол падения при этом будет меньше угла полного внутреннего отражения. В этом случае вся энергия угла вначале линии излучается в окружающее пространство и не распространяется вдоль световода. Это связано с дополнительными непроизводственными потерями энергии.

Промежуточное положение занимают вытекающие волны (волны оболочки).Здесь часть энергии распространяется вдоль световода, а часть её переходит в оболочку и излучается в окружающее пространство. Вытекающие волны образуются в первую очередь, за счет косых лучей. Типы волн привезены на рисунке. Таким образом, в световодах вдоль всей линии распространяется только направляемые (собственные) волны, передающая энергию по линии. Вытекающие и излучаемые волны действуют лишь на начальном участке линии, затем роль их резко уменьшается. Следует иметь в виду, что и при соблюдении угла полного внутреннего отражения Q_n > Q_в часть направляемой энергии просачивается в оболочку и распространя­ется вдоль границы раздела сред в поверхностном слое. Эта просачиваемая волна с удалением от сердечника затухает по экспонициальному закону и проникает в окружающее пространство.

Методика исследования процессов излучения и взаимных полях между волоконными световодами различна для различных режимов работы световодов. Для одномодового и многомодового режимов передачи (d » l) необходимо на основе электродинамики решить систему уравнений связанных волн. Для многомодового режима передачи (d >> l) можно воспользоваться упрощенными законами геометрической оптики.

Переходное затухание на ближнем конце:

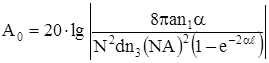
переходное затухание на дальнем конце:

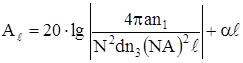
Защищенность от помех:

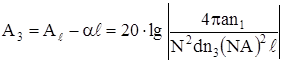
Где:

a – расстояние между центрами влияющего и подверженного влиянию световодов;

d – диаметр световода;

n₁; n₂ – коэффициенты преломления сердцевины и оболочки;

a – коэффициент затухания световода в кабеле dБ/км

NA – числовая апертура;

– длина линии;

n₃ – коэффициент преломления защищенного покрытия;

N – коэффициент ослабления помех;

N = N_n × N_o × N_в

Рис 12

N_n – потери энергии за счет поглощения энергии в оболочке покрытии;

N_o – потери энергии за счет отражения волн на границах сердечник-оболочка, покрытие–воздух;

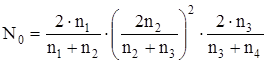
Nв – потери за счет взаимодействия многократно отраженных волн.

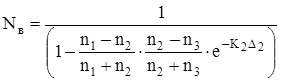
Здесь А₂, А₃ – радиальная толщина оптической оболочки и защитного покрытия;

К2,К3 – параметры затухания в оптической оболочке и защитном покрытии.

,

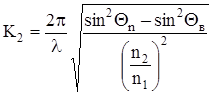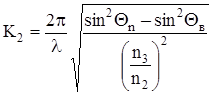
n_n – коэффициент преломления среды между двумя световодами.

Q_n – угол падения волны;

Q_в – угол полного внутреннего