Интегральный признак Коши.

Пусть 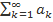- знакоположительный числовой ряд. Составим функцию непрерывного аргумента

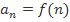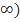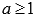y = f(x), аналогичную функции . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале [a; + , где ). Тогда в случае сходимости несобственного интеграла 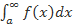сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.

При проверке убывания функции y = f(x) на интервале [a; + 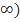,может пригодится теория из раздела возрастание и убывание функции.

Пример 1.

Исследуйте числовой ряд с положительными членами 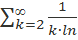на сходимость.

Решение.

Необходимое условие сходимости ряда выполнено, так как 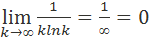. Рассмотрим функцию y= 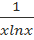. Она положительная, непрерывная и убывающая на интервале [2;+ 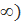. Непрерывность и положительность этой функции не вызывает сомнения, а на убывании остановимся чуть подробнее. Найдем производную: .

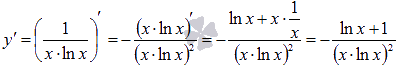Она отрицательная на промежутке [a; + 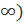,, следовательно, функция убывает на этом интервале.

Таким образом, функция y= 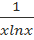удовлетворяет всем условиям интегрального признака Коши. Воспользуемся им:

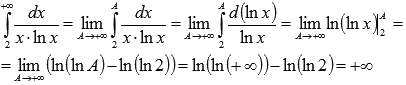
То есть, несобственный интеграл расходится, следовательно, расходящимся является исходный числовой ряд.

Пример 2.

Докажите сходимость числового ряда .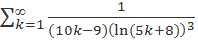

Решение.

Так как 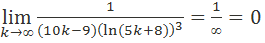, то необходимое условие сходимости числового ряда выполнено.

Начиная с k = 4, справедливо неравенство 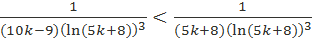. Таким образом, если доказать сходимость ряда 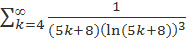, то в силу первого признака сравнения будет сходиться ряд 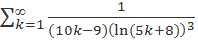тогда из первого свойства сходимости рядов последует сходимость исходного числового ряда.

Итак, осталось доказать сходимость числового ряда .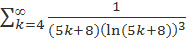

Так как функция y= 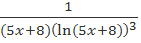положительная, непрерывная и убывающая на интервале 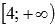(проверить эти факты самостоятельно) то можно воспользоваться интегральным признаком Коши выполнив под интегралом замену переменных типа ln(5x=8)=t или подвести под знак дифференциала выражение (5х+8), которая там представится, как ln(5x+8):

=

=
=-

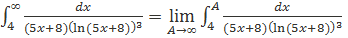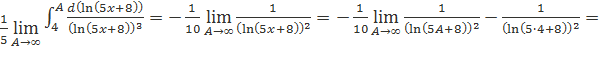
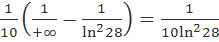
Таким образом, несобственный интеграл 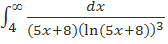сходится, следовательно, сходится исходный ряд Этим доказана сходимость исходного числового ряда.

Абсолютная и условная сходимость.

Вернемся к произвольным числовым рядам A _{= ;}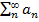

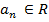
Определение 1.Ряд А называется абсолютно сходящимся, если сходится ряд

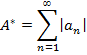
Определение 2. Ряд А называется условно сходящимся, если он сходится, а ряд A^* расходится.