Тепловая модель подогревного термостата. Пусковой режим.

При анализе пускового режима определяется время установления на объекте термостатирования температуры стабилизации с заданной погрешностью. При строгом решении задачи длительность пускового режима т_р берется от начального момента 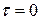, когда температуры всех элементов термостата равны температуре окружающей среды, до момента начиная с которого отклонение 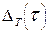температуры объекта от номинальной становится меньше допустимой ошибки термостатирования 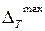(рис. 24.1,а): 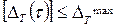Обычно при определении 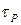делают ряд упрощающих допущений, выделяя в пусковом режиме два этапа.

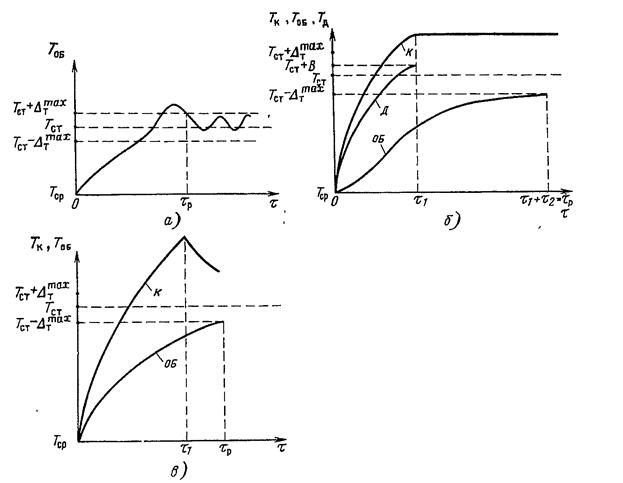
Рисунок 24.1 Временные зависимости температур объекта,

камеры и датчика в пусковом режиме.

Первый этап заканчивается в момент 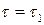когда температура датчика достигает значения 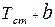и происходит первое отключение нагревателя. При этом полагают, что в момент 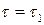температура камеры практически достигает своего среднего значения, которое она имеет в установившемся автоколебательном режиме. В дальнейших расчетах пускового режима пренебрегают малыми колебаниями температуры .камеры и считают, что начиная с момента 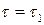она имеет постоянное значение, равное 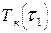(рис. 24.1,б). Тепловую инерцию датчика при анализе первого этапа обычно не учитывают, считая его постоянную времени пренебрежимо малой. В соотношении теплового баланса для камеры пренебрегают тепловым потоком от камеры к датчику.

На втором этапе длительностью 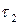температура объекта «подтягивается» к заданному уровню за счет его теплообмена с камерой (рис. 24.1,б).

Заметим, что при таком приближенном определении 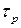не учитывается возможный «выброс» температуры объекта за значение 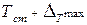процессе установления автоколебаний (рис. 24.1,а и б).

Таким образом, на первом этапе решается система уравнений:

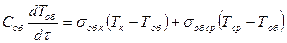; (24.1)

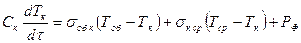; (24.2)

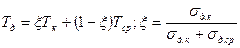; (24.3)

Т_об|_τ=0 = Т_к|_τ=0 = Т_д|_τ=0 = Т_ср,

где Р_ф — мощность, подаваемая в нагреватель термостата в пус­ковом режиме. Если форсированный пусковой режим не предусмотрен, то Р_Ф = Р_тах.

Тогда уравнение для определения τ₁ будет выглядеть следующим образом:

.

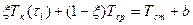Наиболее простую формулу для оценки τ₁ можно получить, считая, что изменение температуры камеры на первом этапе происходит по линейному закону:

τ₁ = (Т_ст + b – Т_ср)С_к/ξР_ф.

На втором этапе решается уравнение (24.1) при τ > τ₁ с условиями Т_об|_τ=τ1 = Т_об(τ₁):

Т_об(τ) = ηТ_к(τ₁) + (1 – η)Т_ср + [Т_об(τ₁) – ηТ_к(τ₁) – (1 – η)Т_ср) exp[ - m_об(τ – τ₁)];

m_об = (σ_об.к + σ_об.ср) / С_об – темп охлаждения объекта.

;

.

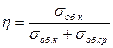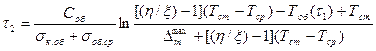Используя в пусковом режиме нагреватель очень большой мощности, можно уменьшить время 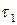практически до нуля. Для 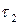существует предельное значение 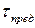, которое будет являться и предельно минимальным значением длительности всего пускового режима.

Эту предельную величину можно получить, считая, что температура камеры скачкообразно принимает значение Т_к(τ₁), и полагая поэтому Т_об(τ₁) =Т_ср:

.

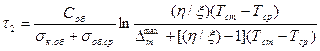Важной задачей является уменьшение длительности пускового режима. В [53] предложен метод ее решения, заключающийся в повышении температуры камеры, при которой происходит первое отключение нагревателя. В этом случае после отключения нагревателя температура камеры начнет уменьшаться, а температура объекта будет продолжать увеличиваться (рис. 24.1, в). Очевидно, момент отключения нужно выбрать так, чтобы произошел одновременный выход температур камеры и объекта на их средние стационарные значения. Формулы для определения значения 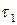, а также для предельной минимальной длительности пускового режима приведены в [53]. Отметим, что 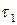зависит от температуры окружающей среды, и поэтому реализация описанной методики приводит к значительному усложнению устройства.