Классическое определение вероятности
Исторически закономерности случайных явлений изучались на материале азартных игр. Азартные игры создавались таким образом, чтобы их исходы были независимы от поддающихся наблюдению условий, то есть были чисто случайными. Схемы азартных игр дают исключительно простые модели для изучения специфических законов случайных явлений, для которых вероятности возможных исходов испытаний можно оценить непосредственно из условий испытаний. Для этого испытания должны обладать симметрией возможных исходов.
Рассмотрим, например, испытание, состоящее в бросании игрального кубика. В силу симметрии кубика есть основания считать, что все шесть возможных исходов испытания одинаково возможны. Это позволяет предполагать, что при многократном бросании кубика все шесть граней будут выпадать примерно одинаково часто. Для правильно выполненного кубика это предположение действительно оправдывается: при многократном бросании кубика каждая его грань выпадает примерно в одной шестой доле случаев бросания. Отклонение этой доли от 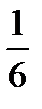 тем меньше, чем больше число испытаний произведено. Для всякого испытания, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.
тем меньше, чем больше число испытаний произведено. Для всякого испытания, в котором возможные исходы симметричны и одинаково возможны, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей.
События, образующие полную группу попарно несовместных и равновозможных событий, называют элементарными. Элементарными событиями, например, являются: появление герба и цифры при бросании монеты; появление 1,2,3,4,5,6 очков при бросании игрального кубика.
Элементарные события такой группы называют благоприятствующими осуществлению события А, если осуществление любого из элементарных событий влечет за собой осуществление события А. Например, появление 2,4,6 очков при бросании игрального кубика благоприятствует осуществлению события А, заключающегося в появлении четного числа очков.
Классической вероятностью Р(А) события А называется отношение числа m элементарных событий, благоприятствующих событию А, к числу n всех элементарных событий, то есть
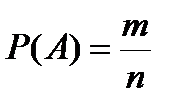 .
.
Задача:
В коробке находится 4 красных и 6 синих карандашей. Наугад извлекаем 1 карандаш. Определить вероятность, что он будет красным.
Решение:
Число элементарных событий, благоприятствующих извлечению красного карандаша событие А, m=4. Общее число элементарных событий n=10.
Вероятность извлечения красного карандаша 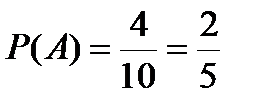 .
.
Дата добавления: 2016-06-05; просмотров: 2263;











