Развитие колебаний в обмотках при воздействии грозовых волн

Волны грозового происхождения, набегающие по линии передачи на подстанцию, приводят к возникновению импульсных напряжений, воздействующих на обмотки трансформатора. В трансформаторе под действием напряжения возникает сложный электромагнитный процесс, приводящий к местным перенапряжениям на изоляции между катушками, между обмотками и изоляцией обмоток относительно заземленных частей. Расчет перенапряжений в обмотках служит основой для выбора изоляционных расстояний в трансформаторах.

Напряжение, воздействующее на одну из обмоток, например ВН, приводит к возникновению в трансформаторе электрического поля, связанного со всеми обмотками. В эксплуатационных условиях обмотка низшего напряжения, как правило, подключена к значительной емкостиотходящих линий или шин. Пренебрегая падением напряжения на этой емкости, будем считать обмотку низшего напряжения заземленной всеми полюсами, т. е. закороченной и заземленной.

Основные закономерности переходных процессов в трансформаторах рассмотрим на простейшей однофазной схеме катушечной обмотки (рис. 8.9,а), на которую воздействует прямоугольная волна (или импульс) u(t)=U₀. В начальный момент времени токи по виткам в силу реакции магнитного потока проходить не могут. На входе обмотки сосредоточивается заряд q_вх=U₀С_вх, где С_вх — входная емкость трансформатора. В электрическом поле заряда q_вх все катушки приобретают некоторый потенциал, спадающий от начала к концу обмотки.

Введем в расчетных целях понятие частичных емкостей катушек на землю ΔС и между соседними катушками ΔК. Тогда при t=0 обмотка изобразится це­почкой емкостей (рис. 8.9,б). Для всей обмотки емкость на землю С= ΔСn, а продольная емкость K= ΔК/n, где n — число катушек в обмотке (емкости ΔС складываются параллельно, а ΔК — последовательно). Обозначим через C₀ и K₀ поперечную и продольную емкости обмотки на единицу длины обмотки. Очевидно, что С₀ = С/l и K₀ = K/l, где l – полная длина обмотки.

Принимая значения ΔС и ΔК (а следовательно, C₀ и K₀) неизменными вдоль цепочки, что приближенно справедливо для обмотки трансформатора, можно выразить распределение напряжения вдоль емкостной цепочки в простых функциях.

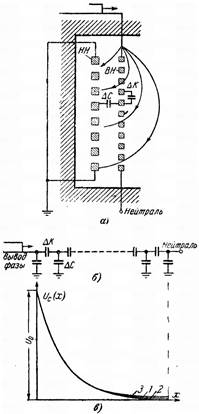
Рис. 8.9 – К расчету распределения потенциалов по обмотке трансформатора в момент t=0. а — схема электростатического поля и емкостные элементы ΔС, ΔК; б — емкостная цепочка замещения обмотки; в — кривые распределения напряжения вдоль обмоткн U_с(х) при заземленной (кривая 2) и изолированной (кривая 3) нейтрали (αl=10). Кривая 1 — результат расчета по приближенной формуле (6.10).

Представим емкостную цепочку длинной линией. Согласно теории длинных линий распределение напряжения U круговой частоты ω вдоль линии (по координате х) имеет вид

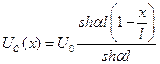(8.6)

если конец емкостной цепочки заземлен, как это имеет место для обмотки трансформатора с заземленной нейтралью, или

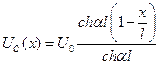(8.7)

если конец емкостной цепочки изолирован, как это имеет место для обмотки трансформатора с изолированной нейтралью.

В этих уравнениях 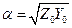— коэффициент распространения,

где Z₀, Y₀— продольное сопротивление и поперечная проводимость линии на единицу длины. В данном случае 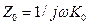и и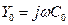, следовательно,

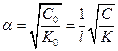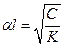; (8.8)

То обстоятельство, что α оказалось независимым от частоты, показывает, что распределение напряжения вдоль емкостной цепочки остается одинаковым при любых частотах, а следовательно, формулы (8.6) справедливы и на фронте прямоугольного импульса (когда возможно замещение обмотки емкостной цепочкой).

Обычно в обмотках С>>К и коэффициент αl;>>1. Выражая в формулах (8.6) гиперболические функции в виде

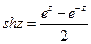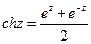; (8.9)

и учитывая, что e^-αl <<l, находим, что на большей части длины емкостной цепочки формула для распределения напряжения приобретает простой вид, соответствующий неограниченно продолженной линии:

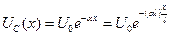(8.10)

Коэффициент αl характеризует крутизну спада кривой емкостного рас­пределения. С увеличением αl спад кривой возрастает. Кривая U_c(x), называемая кривой емкостного распределения напряжения, показана на рис. 8.9,в. В трансформаторах без специальных устройств или специальных обмоток для выравнивания поля значение αl порядка 10—20; при таких значениях αl экспоненциальная кривая U_c(x) спадает весьма быстро. На конце (у нейтрали) обмотки, где хl=1, напряжение совершенно незначительно, что подтверждает возможность расчета в схеме бесконечной цепочки емкостей. Режим работы нейтрали трансформатора практически не оказывает влияния на емкостное распределение напряжения на его обмотке. Входное сопротивление цепочки емкостей (бесконечно продолженной) на частоте ω равно

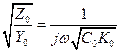(8.11)

откуда следует, что эквивалентная или входная емкость цепочки равна:

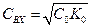(8.12)

Реальные волны имеют фронт некоторой длины, отличной от нуля (t_фр>0). При воздействии таких волн ток на фронте уже проникает в витки обмотки. Увеличение продольного тока эквивалентно в схеме на рис. 8.9 возрастанию емкостей ΔК до некоторого ΔК_э, что ведет к сглаживанию кривой распределения напряжения. Кривая распределения напряжения на фронте таких волн называется кривой начального распределения U_Н(x). Чем положе фронт волны, тем положе и кривая U_Н(x). Для грозовых волн стандартной формы (t_фр=1,5 мксек) кривая U_Н(x) близка к U_c(x).

После затухания переходного процесса принужденное распределение повиткам напряжения U_пр(x) будет определяться э. д. с, наводимой в витках суммарным магнитным потоком. Поскольку обмотка однородна, то и падение напряжения по виткам будет равномерным.

В случае зааземления нейтрали напряжение U_пр равномерно спадает от U₀ до нуля на нейтрали

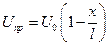(8.13)

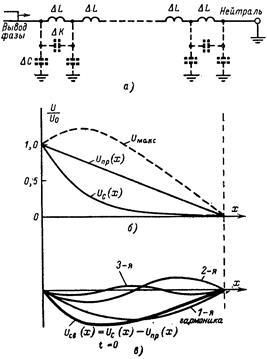
Рис. 8.10 – К расчету распределения максимальных перенапряжений по обмотке трансформатора с заземленной нейтралью. a — схема замещения обмотки для t>0; б — принужденное распределение напряжения по обмотке U_пр(x); в – определение свободной составляющей U_св(x)_t=0, разложение ее на пространственные гармоники и вычисле­ние максимальных перенапряжений.

Для изолированной нейтрали I_пр=0 и, следовательно, принужденное распределение выражается линией, параллельно оси абсцисс U_пр(x)=U₀

Эти зависимости изображены на рис. 8.10,б и 8.11,б. Зная начальное и принужденное распределение напряжения, можно рассчитать свободную составляющую U_св(x) =U_c(x)-U_пр(x) в момент времени t=0 (рис. 8.10,в и 8.11,в). Разложим кривые U_свt=0(x) на пространственные гармоники. На рис. 8.10,в и 8.11,в указаны для простоты по три первые гармоники такого разложения. При заземленной нейтрали потенциалы начала и конца обмотки фиксированы (U₀ и 0), так что свободная составляющая напряжения имеет в этих точках узлы. Поэтому при заземленной нейтрали вдоль обмотки укладываются целые числа полуволн. При изолированной нейтрали фиксированный потенциал, а следовательно, узел свободной составляющей находится лишь в начале обмотки, а на конце обмотки расположена пучность. Поэтому при изолированной нейтрали вдоль обмотки укладываются целые нечетные числа четвертей волн. Амплитуды гармоник A_k определяются разложением в тригонометрический ряд кривой U_свt=0(x). Эти амплитуды равны для заземленной нейтрали

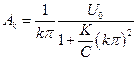(8.14)

и для изолированной нейтрали

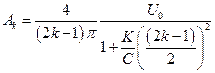(8.15)

где k=1,2,3...

Каждая пространственная гармоника (стоячая волна) колеблется во времени около нулевого значения, т. е. около оси абсцисс. При равенстве периодов колебаний гармоник T_h = T и отсутствии затухания сумма всех гармоник в любой момент времени дает кривую u_св(x,t) переменной амплитуды, но сохраняющую свою форму. Через время t = T/2 кривая u_св(x,t) достигает значения U_св(x)_t=0, но с обратным знаком. Арифметически складывая ординаты этой кривой и кривой U_пр(x), мы находим максимальные напряжения в обмотке U_м(x). Такое построение, показанное на рис. 8.10,б и 8.11,б пунктиром, часто используется для быстрой приближенной оценки максимальных напряжений.

В действительности периоды колебаний пространственных гармоник снижаются с порядковым номером гармоник. Колебания гармоник происходят с затуханием, причем с увеличением порядкового номера гармоники затухание вследствие поверхностного эффекта резко возрастает. К моменту времени Т₁ когда перваягармоника напряжения достигает максимального значения, высшие гармоники уже успевают в значительной степени затухнуть.

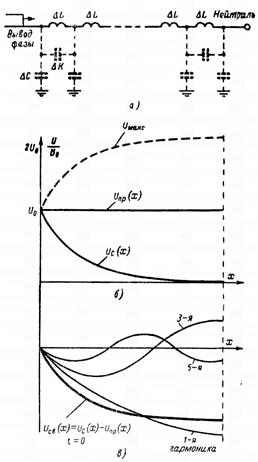
Рис. 8.11. То же, что и на рис. 8.10, но для изолированной нейтрали.

Затухание первой гармоники в момент t = T₁/2 учитывается умножением ее амплитуды на коэффициент 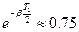, найденный путем усреднения ряда экспериментальных значений.

Таким образом, распределение максимальных напряжений в обмотке U_м(x) находится путем наложения на кривую U_пр(x) первой гармоники U_св(x), взятой с обратным знаком по отношению к моменту t = 0 и умноженной на коэффициент 0,75.

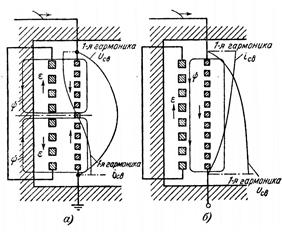
Рис. 8.12 – Пространственное расположение первой гармоники напряжения и тока собственных колебаний в первичной обмотке и поток и э.д.с. во вторичной обмотке. а – первичная обмотка с заземленной нейтралью: б – первичная обмотка с изолированной нейтралью.

Если на трансформатор воздействует импульс длиной t_B, то напряжения в обмотке достигают максимальных значений при условии t_B> T₁/2. Если t_B<< T₁/2, то колебания основной гармоники в обмотке не успевают развиться и напряжения в обмотке остаются близки к кривой первоначального распределения U_H(x).

Значение Т₁ определяется емкостью обмотки и ее индуктивностью для тока свободных колебаний. Для трансформаторов напряжением 110 кВ и выше Т₁ лежит в пределах 50 – 100 мкcек. Рассмотрим влияние на Т₁ состояния вторичной обмотки трансформатора. С этой целью выделим первую гармонику напряжения и тока собственных колебаний первичной обмотки. Ток гармоники отстает от напряжения на 1/4 пространственного периода (рис. 8.12). При заземленной нейтрали ток основной гармоники имеет узел в середине обмотки и пучности по концам: при изолированной нейтрали узел тока расположен на нейтральном конце.

С колебательной составляющей тока в первичной обмотке связан магнитный поток Ψ, пересекающий вторичную обмотку и наводящий э.д.с. ε в ее витках. При заземленной нейтрали э.д.с. в витках вторичной обмотки взаимно компенсируются (рис. 8.12,а) и, следовательно, ток по виткам этой обмотки проходить не будет. Это означает, что магнитный поток основной гармоники почти не встречает реакции вторичной обмотки и, следовательно, свободно проникает в сталь магнитопровода, не образуя, однако, главного магнитного потока. Поэтому размыкание или замыкание вторичной обмотки практически не оказывает влияния на магнитный поток и, следовательно, на значение Т₁.

При изолированной нейтрали э.д.с. в витках вторичной обмотки направлены в одну сторону (рис. 8.12,б), что вызывает протекание в короткозамкнутой вторичной обмотке тока, вытесняющего магнитный поток основной гармоники. При размыкании вторичной обмотки это вытеснение прекращается и поток первичной обмотки проникает в сталь магнитопровода, образуя главный магнитный поток, что резко увеличивает индуктивность первичной обмотки. В результате размыкание вторичной обмотки приводит к увеличению Т₁ в десятки раз.

Указанные выше значения Т₁ (50 – 100 мксек) относятся к обмоткам с заземленной нейтралью либо к обмоткам с изолированной нейтралью при короткозамкнутой вторичной обмотке.

Напряжения, развивающиеся в процессе колебаний, воздействуют на главную изоляцию обмоток. Как следует из изложенного, при заземленной нейтрали максимальные перенапряжения возникают вблизи линейного конца, а при изолированной нейтрали — в нейтрали. При установке в нейтрали разрядника уровень напряжения в нейтрали ограничивается характеристиками разрядника. Обычно этот уровень весьма мал, и поэтому переходные процессы в обмотках с разрядником в нейтрали развиваются, как в обмотках с заземленной нейтралью.