Радиальное электрическое и тепловое поля в одножильном кабеле с круглой жилой

Распределение потенциала в электрическом поле может быть получено после решения уравнения (7.6):

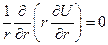(7.7)

Проинтегрировав это уравнение, получим:

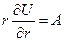(7.8)

где А — постоянная интегрирования.

При r=r₀ U=U₀ где r₀— радиус жилы;

U₀ – потенциал жилы.

Если потенциал оболочки принять равным нулю, то после интегрирования уравнения (5.8) получим:

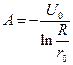(7.9)

где R — радиус кабеля по изоляции.

Подставив величину A в уравнение (7.7) и учитывая, что E=–dU/dr получим

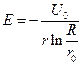(7.10)

Полученое уравнение справедливо лишь при постоянных электрических параметрах среды. Если среда неоднородна, то для простейшего случая радиального поля можно не решать общие сложные уравнения, а получить расчетные формулы более простым способом, который приводится ниже.

Изоляционная среда характеризуется электрическими параметрами: относительной диэлектрической проницаемостью ε и удельным объемным сопротивлением или удельной электропроводностью ρ_v = 1/γ. В неоднородной среде в первый момент после включения постоянного напряжения напряженность поля распределяется в соответствии с диэлектрической проницаемостью неоднородностей. С течением времени на границах неоднородностей появляются поверхностные заряды, процесс накопления которых вызывает ток абсорбции. В установившемся режиме напряженность поля распределяется в соответствии с проводимостью неоднородностей.

Постоянная времени переходного процесса накопления зарядов внутри изоляции зависит главным образом от электрических свойств, а также от формы и размеров неоднородностей и по порядку величины совпадает с произведением εε₀ρ_v для изоляции.

При переменном напряжении, если постоянная времени значительно больше полупериода (εε₀ρ_v>>1/(2f)) объемные заряды не успевают накапливаться и напряженность поля распределяется в соответствии с ε; при (εε₀ρ_v<<1/(2f)) процесс накопления зарядов успевает завершиться полностью и напряженность поля распределяется в соответствии с проводимостью (при постоянном токе). Если εε₀ρ_v≈1/(2f) то необходимо исследовать неустановившийся режим накопления зарядов внутри диэлектрика. Но такой случай в силовых кабелях (при промышленной частоте) может иметь место только в полупроводящей среде.

Таким образом, в первом случае имеет место соотношение

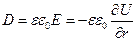(7.11)

где D – электрическое смещение

Во втором случае

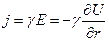(7.12)

где j – плотность тока в изоляции.

Для плотности теплового потока можно записать

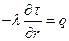(7.13)

где превышение температуры в изоляции над температурой оболочки τ=T-T_об

T_об – температура оболочки;

q – тепловой поток через единицу поверхности в единицу времени.

Очевидна аналогия D~j~q и 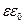~j~λ

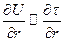U~T (7.14)

Соответственно для уравнений (7.11)-(7.13) можно записать интегральные соотношения:

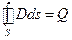(7.15)

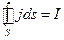(7.16)

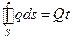(7.17)

где S – замкнутая поверхность;

Q – заряд внутри поверхности S;

I – общее число зарядов, вытекающих из объема, ограниченного S (общий ток утечки);

Qt – общее количество тепла, выделяющееся внутри S.

При решении уравнения (7.15) будем предполагать, что диэлектрик не имеет объемных зарядов, а при решении уравнения (7.17) – что он не имеет источников тепла.

Выберем поверхность S в виде концентрического цилиндра с образующей, равной единице длины кабеля, Если поле радиально, то при цилиндрической поверхности величины D, j и τ могут быть вынесены за знак интеграла. При этом решение уравнений (7.15) – (7.17) можно получить в следующем виде:

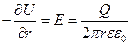(7.18)

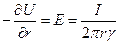(7.19)

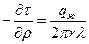(7.20)

где Q — заряд;

I — общий ток утечки из жилы через изоляцию;

P_ж = Qt — потери энергии в жиле.

Все величины относятся к единице длины кабеля.

Уравнения для всех трех полей одинаковы, поэтому с учетом аналогии (7.14) достаточно привести решение дли одного из этих случаев.

Проинтегрируем уравнение (7.18) и подставим в качестве пределов радиусы по жиле и изоляции. Получим соотношение между зарядом на жиле и ее потенциалом;

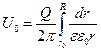(7.21)

Подставив значение Q из уравнения (7.18) в (7.21), получим:

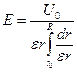(7.22)

и для емкости кабеля

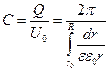(7.23)

При ε = const емкость единицы длины кабеля вычисляется по формуле

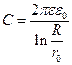(7.24)

Проинтегрировав (7.19), аналогичным образом получим формулы для постоянного тока;

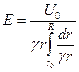(7.25)

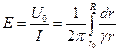(7.26)

а при γ = const сопротивление изоляции на единице длины кабеля

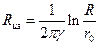(7.27)

Для теплового поля из уравнения (7.20) при λ = const можно записать:

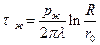(7.28)

где τ_ж — превышение температуры жилы над температурой оболочки. В соответствии с уравнением (7.28) можно ввести понятие о тепловом законе Ома :

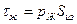(7.29)

где τ_ж соответствует напряжению, 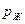— току и S_из — сопротивлению, причем из уравнения (7.28) следует, что тепловое сопротивление единицы длины кабеля

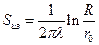(7.30)

Из уравнений (7.20) и (7.28) можно получить зависимость превышения температуры в изоляции от радиуса кабеля:

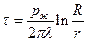(7.31)

Таким образом, к аналогии (7.14) после сравнения уравнений (7.24), (7.26) и (7.30) можно добавить аналогию

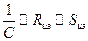(7.32)

Величину 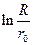— можно рассматривать как геометрический коэффициент (фактор) G, который зависит только от конфигурации электродов.

Из теории поля известно, что если поле подчиняется уравнению Лапласа, то при любой конфигурации электродов для однородной среды геометрический коэффициент будет одинаковым для электрического поля смещения, проводимости, а также для теплового поля. При этом достаточно знать одну из величин аналогии (7.32), чтобы рассчитать обе другие.

Если изоляционная среда неоднородна, то геометрический фактор будет одинаковым при условии, что зависимость параметров среды от радиуса будет одинаковой.