Двухпроводные направляющие системы

3.1 Основное уравнение однородной кабельной цепи

Качество передачи по кабельным линиям связи и их электрические свойства полностью характеризуются первичными параметрами кабеля: активным сопротивлением R, индуктивностью L, емкостью C и проводимостью изоляции G. Эти параметры определяются лишь конструкцией кабеля, используемыми материалами и частотой тока.

По физической природе параметры кабеля аналогичны параметрам колебательных контуров, составленных из элементов R,L, и C. Разница состоит лишь в том, что в контурах эти параметры (G,L и C) являются сосредоточенными, а в кабелях они равномерно распределены по всей длине цепи.

3.1.2 Эквивалентная схема кабельной линии

Параметры R и L, включенные последовательно (продольные), образуют суммарное сопротивление 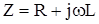, а параметры G и C (поперечные) суммарную проводимость 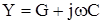. Из указанных четырех первичных параметров кабеля лишь R и G обуславливаю потери энергии первый - потери на тепло в ТПЖ и других металлических частый кабеля (экран, оболочка, брони), второй - потери в изоляции.

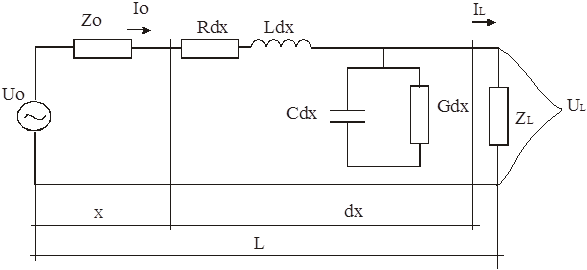Рис 1. Однородная кабельная цепь

Рассмотрим однородную кабельную цепь с первичными параметрами R, L, C и G

В начале цепи включен генератор сопротивлением Z₀ в конце нагрузка Z_L. Обозначим напряжение и ток в начале цепи U₀, I₀, в конце U_L, I_L.

Выделим на расстоянии x от начала цепи бесконечно малый участок dx. Обозначим силу тока, протекающего по элементу цепи dx, через I и напряжение между проводниками через U. Тогда падение напряжения на dx будет:

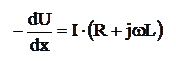(1)

Знак минус перед производными в левой (1) части уравнений означает, что U и I с увеличением x уменьшаются. Утечка тока на участке dx:

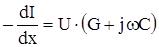(2)

Для решения этих уравнений относительно U и I исключим сначала I из (1), взяв вторую производную:

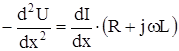
Подставим это выражение в (2) и получим:

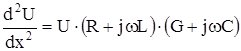(3)

обозначим: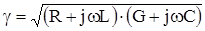

тогда: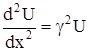

Решение этого уравнения имеет вид: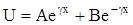

дифференцирую это уравнение, получим выражение для тока:

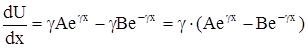
Подставив это выражение в (1), получим:

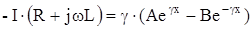
или, обозначив

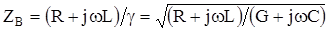(5)

имеем:

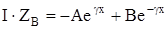
Таким образом, имеем два уравнения с двумя неизвестным А и В:

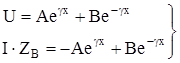(6)

Для нахождения постоянных А и В воспользуемся значениями тока и напряжения в начале цепи (при x=0) I₀ и U₀. Тогда (3.1.6) примут вид:

отсюда:

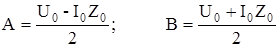(7)

подставив значение А и В в (6), получаем:

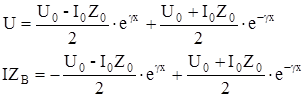
Производя соответствующие преобразования и с учетом того, что:

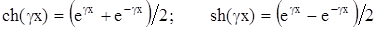
получим значения напряжения Ux и тока Ix в любой точке цепи:

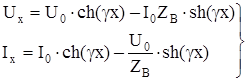(8)

В конце цепи при x = L получим:

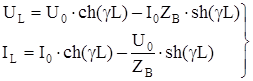(9)

Практически, оказывается, удобно пользоваться выражениями, устанавливающими зависимость напряжения и тока вначале цепи от напряжения и тока в конце цепи.

Решив (9) относительно U₀ и I₀ получим:

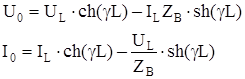(10)

Уравнения (8) – (10) устанавливают взаимосвязь токов и напряжений с параметрами цепи R, L, C и G или Y и Z_B, позволяя определить напряжение и ток в любой точке цепи в зависимости от значений U и I в начале или в конце. Эти уравнения справедливы при любых нагрузках Z₀ и Z_L по концам цепи.

При согласованных нагрузках (Z₀=Z_L=Z_B) U₀ /I₀=U_L/I_L=Z_B уравнения (8)–(10) упрощаются и принимают вид:

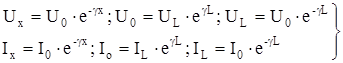(11)

Практически наиболее часто пользуются уравнениями в виде:

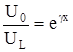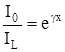и (12)

В этом случае отношение мощностей в начале и конце линии имеет вид:

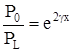(13)

Таким образом, получены уравнения однородной кабельной цепи в общем, виде при любых нагрузках по концам, формулы: (8) – (10), и при согласованных нагрузках, формулы: (11) – (13).

Из приведенных формул следует, что распространение энергии по линии, ток и напряжение в любой точке цепи обусловим двумя параметрами Y и Zв.

3.2 Вторичные параметры двухпроводных

направляющих систем

Вторичными параметрами линии являются сопротивление Zв и коэффициент распространения Y. Они широко используются для оценки эксплуатационно-технических качеств линии связи. При проектировании, сооружении и эксплуатации кабельных линий в первую очередь корректируются и контролируются именно вторичные параметры линии.

3.2.1 Волновое сопротивление Zв

Это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т.е. при условии отсутствия внимания на процесс передачи несогласованности нагрузок по концам линии; Zв свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.

Количественное соотношение, имеющие место между волной напряжения и волной тока в линии, и есть волновое сопротивление цепи. При этом, как следует из данного определения волнового сопротивления, необходимо рассматривать лишь падающую (движущуюся вперед) электромагнитную волну: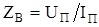

Если в линии выделить отдельно отраженную волну, то она, двигаясь к началу линии, также будет встречать сопротивление, равное волновому: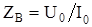

Волновое сопротивление рассчитывается по формуле:

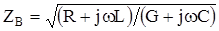
По всей физической природе, что также следует и из приведенной формулы, значение Zв не зависит от длины кабельной линии и постоянно в любой точке цепи.

В общем виде волновое сопротивление является комплексной величиной и может быть также выражено через его действительную и мнимую части:

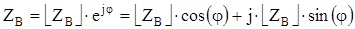
на практике величину волнового сопротивления оговаривают в ГОСТе, при этом величина Zв по длине должна быть одинаковой, то поскольку практически не выполнимо то в ГОСТе задаются пределы 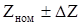, пример 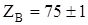Oм.

3.2.2 Коэффициент распространения

Электромагнитная энергия, распространяясь вдоль кабельной линии, уменьшается от начала к концу линии. Уменьшение, или затухание, энергии объясняется потерями её в цепи передачи. Следует различать два вида потерь энергии. Во-первых, потери в металлических элементах кабеля и во-вторых, потери в изоляции.

Потери в цепи передачи учитываются через коэффициент распространения Y, который является комплексной величиной и м.б. представлен суммой действительной и мнимой её частей:

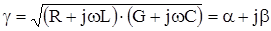
Тогда уравнение для тока и напряжение можно представить в следующем виде:

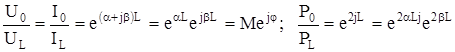
Модуль этого выражения 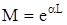характеризует уменьшение абсолютного значения тока или напряжение при прохождении по линии длиной L. Угол 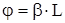характеризует изменение угла векторов тока или напряжение на этом же участке линии длиной L.

При передаче сигналов связи параметры a и b характеризуют соответственно затухание и изменения фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.

Логарифмируем обе части приведенных выше выражений, получаем формулы для расчета затухания:

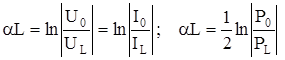
Затухание цепи связи (a=aL) принято оценивать в неперах (Нп) или децибелах (дб). Для неперов используется натуральная система логарифмов, а для децибелов (бело) -десятичная. Затухание в 1 Нп соответствует уменьшение мощностей 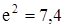раза, а для U или I в 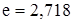раза.

Это вытекает из:

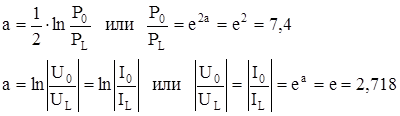
Затухание в 1 дБ характеризует уменьшение по мощности в 1.26 раз, а по току или напряжению в 1.12 раза:

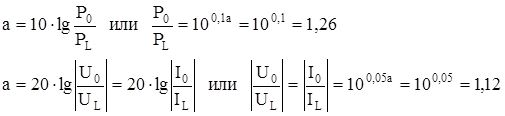
Между неперами и децибелами существует следующее соотношение:

I0

т.е.

На рис.2. показан характер изменения тока вдоль однородной кабельной линии. Как видно из графика, вектор тока уменьшается и изменяет фазу вдоль линии. Уменьшение тока происходит по экспоненциальному закону.

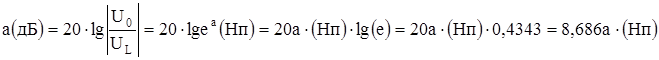
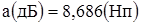
Рассмотрим зависимость вторичных параметров кабельной линии от частоты. Для упрощенного анализа этой зависимости выразим вторичные параметры кабельных линий Zв и Y сокращенными формулами, которыми можно пользоваться для расчетов.

При постоянном токе (f=0):

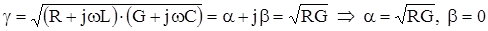
В диапазоне низких частот (f=800 Гц) учитывая, что индуктивность кабельных цепей невелика, в указаном частном диапазоне пренебрегаем значением wL по сравнению с R. В этом случае можно также не считаться с параметром G по сравнению с wС, т.е. в низкочастотном диапазоне R>wL и G>wC, тогда:

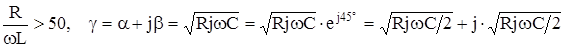
Следовательно: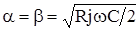

В свою очередь: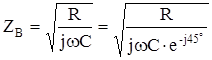

Выразим a и b через первичные параметры передачи R, L, G и C:

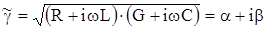
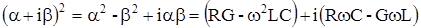
отсюда: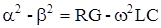

можно записать, что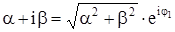

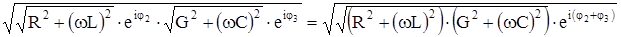
отсюда: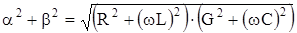

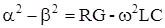
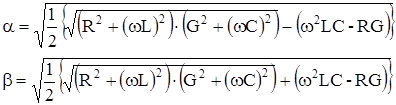
При высоких частотах (~> 60 Кгц), когда 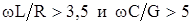формула для a и b может быть упрощена, для этого запишем:

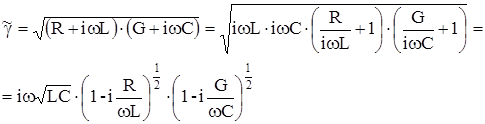
Раскладывая двучлены, заключенные в скобки, в биноминальные ряды:

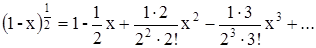
и в силу малости x ограничиваясь только двумя первыми членами, ряда и пренебрегая малыми членами, запишем:

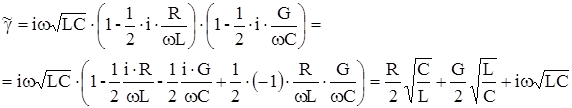
Откуда: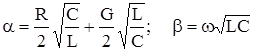

В диапазоне высоких частот 30 Кгц и выше. При высококачественной передаче по кабельной цепи имеют место следующие соотношения: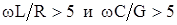

Тогда, применив к выражению g формулу бинома Ньютона, и ограничившись первыми 2-мя членами разложения, получим:

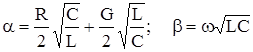
Волновое сопротивление в этом случае можно рассчитывать по формуле:

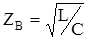
Во всех остальных случаях коэффициент затухания и фазы, и также волновое сопротивление следует производить по полным формулам.

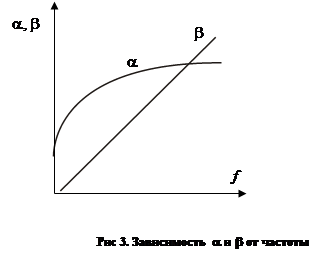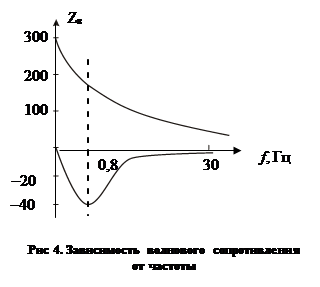
Модуль волнового сопротивления с ростом частоты уменьшается от значения 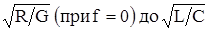и сохраняет это значение во всей области высоких частот. Угол волнового сопротивления равен нулю при f=0, и на высоких частотах, а на средних (f=800 Гц) имеет максимальное значение. В кабельных линиях угол всегда отрицательный и не превышает –45°, что свидетельствует о преобладании емкостной составляющей и емкостном характере волнового сопротивления.

3.2.3. Скорость распространения электромагнитной

энергии по кабелям.

Скорость передачи зависит от параметров цепи и частоты тока. Она определяется следующей формулой: 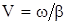. Т.о., если затухание цепи a определяет качество и дальность связи, то коэффициент фазы b обусловливает скорость движения энергии по линии.

В диапазоне высоких частот, когда 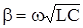скорость не зависит от частоты и определяется лишь параметрами кабеля 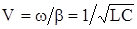, при этом V~200000 км/с

При постоянном токе 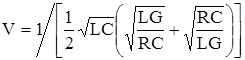, V~10000 км/с

3.2.4. Волновое сопротивление

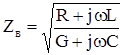, приведем к виду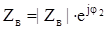

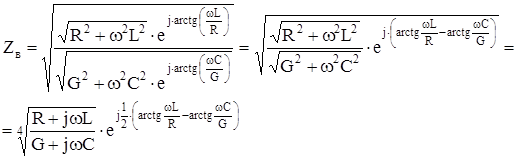
Таким образом получается:

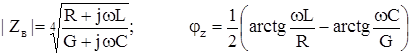
3.2.5. Качество передачи и дальность связи

по кабельным линиям

Дальность связи определяется по формуле:

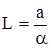
где величина затухания а(dB) для соответствующих кабельных линий ограничивается, а коэффициент затухания a полностью зависит от первичных параметров и частоты. Например, затухание между 2-мя абонентами не должно быть больше 28,7dВ. Кроме того, существуют нормы на время прохождения сигнала:

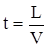
3.3 Свойства неоднородных линий

3.3.1 Падающие, отраженные и стоячие волны

Основные уравнения передачи показывают, что процесс передачи энергии в линии имеет волновой характер и может быть представлен в виде падающих и отраженных волн.

Из уравнений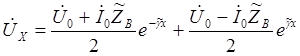

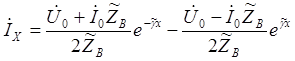
Можно написать следующее выражение для падающих и отраженных волн напряжения и тока в конце линии. (x = l)

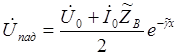
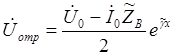
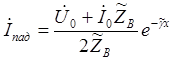
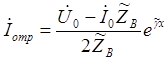
Тогда уравнения передачи можно записать в форме:

; (*)

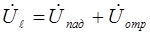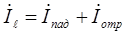Имея ввиду, что

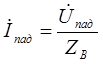и ,

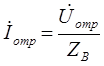получим:

,

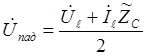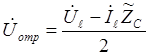
Аналогичные зависимости можно получить и для тока :

;

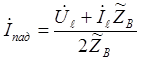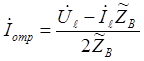
Отношение напряжения или тока отраженной волны к напряжению или току падающей волны называется коэффициентом отражения p.

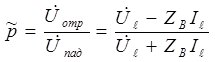
И с учетом что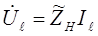

где Zн – сопротивление нагрузки, получим:

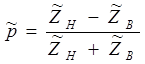
Модуль коэффициента p для пассивных систем не превышает 1. Когда p вещественен и положителен, это значит, что падающая и отраженная волны совпадают по фазе. Когда p вещественен и отрицателен, это значит, что обе волны находятся в противофазе, мнимость p означает сдвиг фаз на .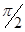

Сравнивая между собой уравнения (*) можно сказать, что коэффициент отражения по току будет отличаться знаком от коэффициента отражения по напряжению.

Если Z_L = 0 , т.е. при коротком замыкании линии коэффициент отражения р = -1 , при Z_L = 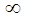, т.е. при холостом ходе р = 1. А если Z_L= Z_В , то р = 0. В последнем случае отраженных волн в линии не будет и в линии будет режим бегущей волны. Этот режим наиболее эффективен.

Случай когда р = 1 называется полным отражением. При этом амплитуды отраженной и падающей волн равны. При сложении одинаковых амплитуд падающей и отраженных волн синусоидального напряжения образуется стоячая волна напряжения, а при сложении падающих и отраженных волн тока – стоячая волна тока. В точках, где сказывается максимальное значение падающей и отраженной волн тока или напряжения будут кучности тока или напряжения, а в точках, где эти значения вычитаются, будут узлы тока или напряжения.

В стоячей волне амплитуда колебания является периодической функцией координаты, а в бегущей волне амплитуда колебаний постоянна. Другим отличающим признаком стоячей волны является то, что фаза колебаний стоячей волны постоянна на участке между двумя узлами, и вдоль всей линии фаза меняется, периодически принимая попеременно значения 0 и .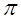

В бегущей волне фаза колебаний является ……….функцией координаты.

При нагрузке линии на активной, сопротивление р будет величиной действительной. Величина напряжения в кучности (максимум напряжения) будет равна

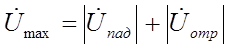
А в узле (минимум напряжения) будет равна

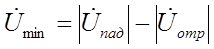
Максимум напряжения (кучности) и минимум напряжения (узлы) будут отстоять друг от друга на расстоянии x/2.

Имеется в виду , что 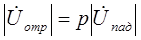, можно написать

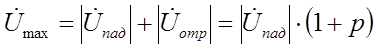
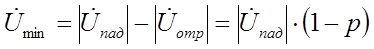
Отношение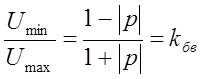

Где k_бв – коэффициент бегущей волны

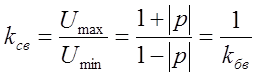
Где k_св – коэффициент стоячей волны, является мерой рассогласования

k_б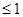в , k_св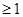

Зная величины k_бв или k_св можно легко определить затухание линии на высоких частотах. Для этого необходимо подключить генератор к коротко замкнутой линии и определить амплитуды. U_пад и U_отр . Тогда затухание линии длиной 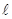определяется

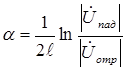, имея в виду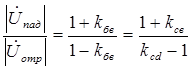

получим 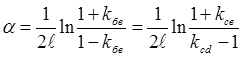, Нп/м

Коэффициенты бегущей и стоячей волн имеет большое значение в технике линий высоких частот. Зная, например, КСВ и КБВ , можно определить на высоких частотах затухание линии. Для этого необходимо подключить генератор к короткозамкнутой линии и определить амплитуду падающей и U_пад и отраженной волн U_отр напряжения. Тогда коэффициент затухания линии, длиной 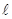определяется (при условии Zо = Zв).

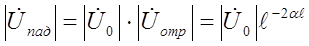
откуда ,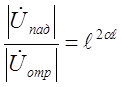

откуда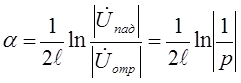

КБВ=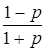

KБВ(1+p)=1-p КБВ+p*КБВ=1-p

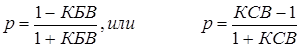
откуда 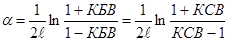, Нп/м

3.3.2 Входное сопротивление и рабочее затухание

кабельной линии

Входным сопротивлением Zвх называется сопротивление, измеренное на входе линии при любом нагрузочном сопротивлении на ее конце. Значение Zвх определяется отношением напряжения Uo к току Io в начале линии и в общем виде может быть получено

,

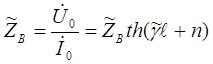где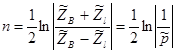

Если линия имеет согласованную нагрузку (Z_L = Zв) , то Z_ВL = Z_В и р = 0. Для электрически длинной линии ( 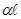> 13дБ) при любой нагрузке на ее конце Zвх = Zв.

Зависимость входного сопротивления кабеля от частоты показана на рис.1, при нагрузочном сопротивлении Z_L = 2Zв.

Входное сопротивлении линии в отличие от волнового сопротивления зависит от длины линии и сопротивления нагрузки. Это объясняется тем, что при несогласованной нагрузке (т.е. при Z_L не равное Zв) в линии возникают отраженные волны, которые, взаимодействуя с падающими изменяют соотношения напряжения и тока в начале линии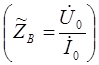

Для электрически длинных линий ( 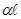> 13 дБ) Zвх = Zв.

Рабочее затухание а_р является затуханием кабельной цепи в рабочих условиях, т.е. при любых нагрузочных сопротивлениях (Zо и Z_L ) на концах линии. Оно представляет более общий параметр, т.е. кроме собственного затухания кабеля а = 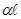, учитывая также влияние несогласованности на стыках кабеля Zв с нагрузочной Zo и Z_L.

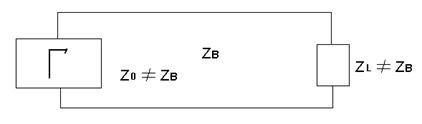Ранее было получено

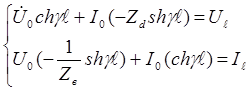
Решим данное уравнение относительно Uo и Io, считая известным U_L и I_L, найдем определитель

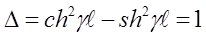
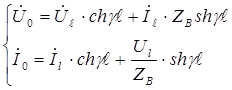
Величина волнового сопротивления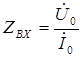

,

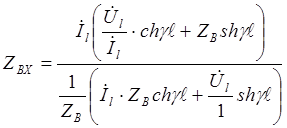
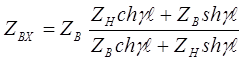где 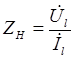- сопротивление нагрузки.

Преображаем выражение для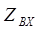

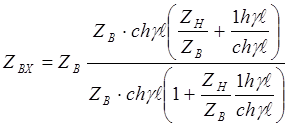
обозначим ,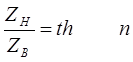

тогда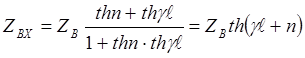

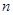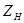ч/з и 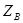может быть получено следующим образом

,

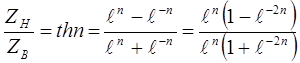откуда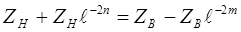

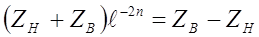
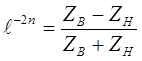, откуда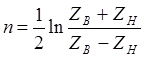

Рабочее затухание рассчитывается по формуле

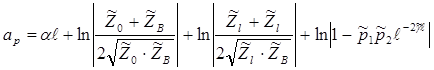
Где р1 и р2 – коэффициенты отражения на стыках «генератор кабель» и «приемник кабель»

Выражение состоит из четырех слагаемых : первое выражает собственное затухание кабеля 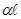, второе и третье – дополнительные затухания в следствии несогласованности сопротивления генератора и кабеля 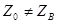, а так же приемника и кабеля 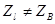; четвертое слагаемое равно дополнительному затуханию от взаимодействия несогласованности в начале и в конце линии. (а_р всегда больше )

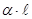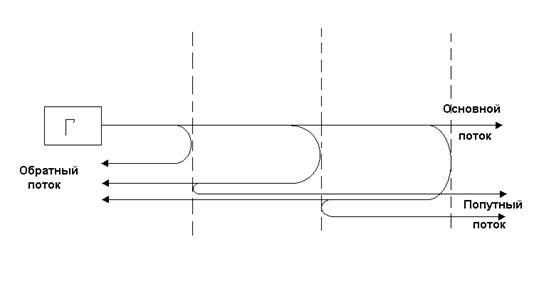
3.3.3 Линии неоднородные по длине

Различают неоднородности внутренние – в пределах строительной длины кабеля и стыковые – обусловленные различием характеристик сопрягаемых строительных длин. Стыковые неоднородности, как правило, превышают внутренние. Неоднородность кабеля сказывается главным образом на волновом сопротивлении кабеля, величина которого на участках неоднородности отличается от номинальной. Неоднородности цепи учитываются через коэффициент отражения.

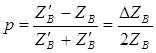
Zв и Z`в – волновые сопротивления соседних неоднородных участков кабеля; 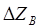- величина отклонения волнового сопротивления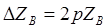

Реальный кабель можно рассматривать как неоднородную цепь, составленную из отдельных участков. Э/м волна распространяясь по такому кабелю и встречая на своем пути неоднородность, частично отражается от нее и возвращается к началу линии. При наличии нескольких неоднородных участков волна претерпевает серию частичных отражений и циркулируя на линии , вызывает дополнительное затухание и искажение характеристик цепи.

Неоднородности в кабели приводят к появлению в цепи двух дополнительных потоков энергии: обратного, состоящего из суммы элементарных отраженных волн в местах неоднородностей и движущегося к началу цепи; и попутного, возникающего по закону двойных отражений.

Обратный поток приводит к колебаниям входного сопротивления кабеля Zвх, т.е. характеристика Zвх становится волнообразной. Это затрудняет согласование кабеля с аппаратурой на концах линии и приводит к искажениям в цепи передачи. Попутный поток искажает форму передаваемого сигнала и создает помехи в передаче.

Следует иметь в виду, что в аналоговых системах передачи с частотным разделением каналов попутный поток надо учитывать по всей длине линии. В цифровых системах передачи с временным разделением каналов попутный поток …….длиной регенерационного участка. С целью повышения однородности кабельной линии связи производится группирование строительных длин, и они прокладываются с таким расчетом, чтобы отношение электрических характеристик не превышало определенных значений. Коаксиальные кабели группируются по величинам волновых сопротивлений, а симметричные – по электрической емкости.

3.3.4 Качество передачи и дальность связи

по кабельным линиям

Дальность связи по кабельной линии обуславливается затуханием самого кабеля и свойствами аппаратуры.

Если известно усилительная способность передатчика и, в первую очередь, перекрываемое аппаратурой затухание а, то дальность связи l определяется по формуле

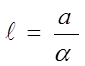
Где 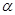-коэффициент затухания кабельной цепи. По существующим нормам затухание между двумя абонентами не должно превышать 28,7 дБ (3,3 Нп).

Распределение затухания по участкам тракта в случае нахождения абонентов в пределах одного города показано на рис.7

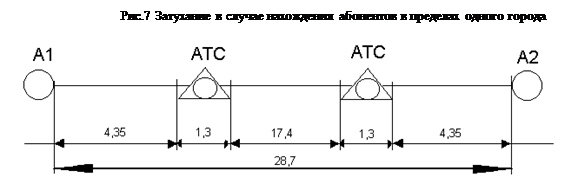Затухание разговорного тракта между абонентами, находящимися в разных городах показано на рис.8.

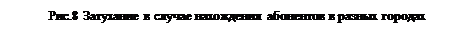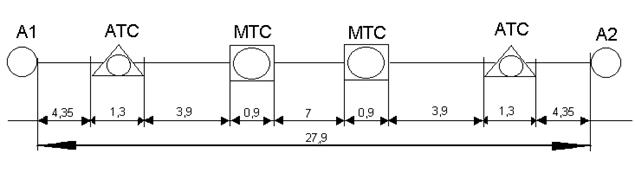
Общепринятым методом увеличения дальности связи по кабельным линиям является последовательное включение в линию усилителей, компенсирующих затухание цепи.

Для удаления связи большую часть усилительных пунктов делают необслуживаемыми (НУП) и лишь часть обслуживаемыми (ОУП). Обычно на магистральных линиях между двумя ОУП располагается 10-20 НУП. Расстояние между НУП – 10-20 км.

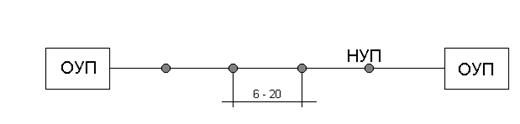
Наряду с затуханием существенным фактором влияющим на дальность и качество связи является время распространения сигнала по линии. По нормам оно не должно быть больше 250 мс.