Поле магнитного диполя.
Для облегчения решения задач магниторазведки вводится понятие магнитного потенциала точечной магнитной массы
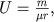
| (2.4) |
где  - расстояние от центра магнитной массы до точки наблюдения.
- расстояние от центра магнитной массы до точки наблюдения.
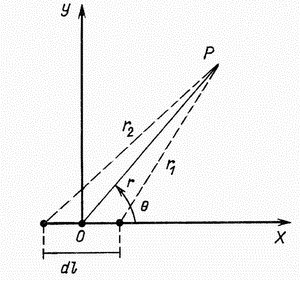
В теории магнетизма пользуются понятием магнитного диполя, т.е. двух равных, близко расположенных магнитных масс противоположного знака (рис. 2.3). Потенциал диполя 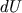 выражается формулой
выражается формулой
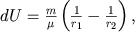
|
где 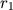 и
и 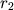 - расстояния от центра магнитных масс до точки наблюдения.
- расстояния от центра магнитных масс до точки наблюдения.
|
| Рис. 2.3. Магнитный диполь |
Выразив с помощью теоремы косинусов 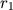 и
и 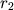 через
через  ,
, 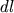 , и
, и 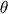 , можно записать
, можно записать
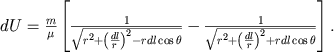
|
Разделив числитель и знаменатель на  и используя формулу бинома Ньютона, получим
и используя формулу бинома Ньютона, получим
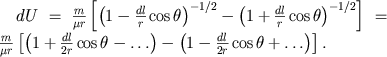
|
Поскольку 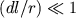 , то всеми степенями выражения
, то всеми степенями выражения 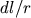 , большими единицы, можно пренебречь, и формула потенциала диполя упростится:
, большими единицы, можно пренебречь, и формула потенциала диполя упростится:
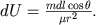
|
Или, заменив 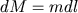 , получим окончательное выражение для потенциала диполя
, получим окончательное выражение для потенциала диполя
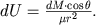
|
Из выражения для потенциала диполя нетрудно получить составляющие поля 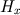 и
и 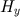 и полный (
и полный ( 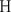 ) вектор напряженности. Заменив
) вектор напряженности. Заменив 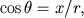 можно записать:
можно записать:
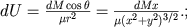
|
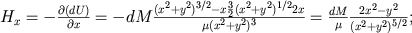
| (2.5) |
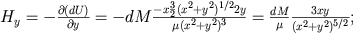
|
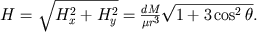
|
В частности, на протяжении оси диполя ( 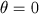 )
) 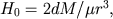 на перпендикуляре к оси диполя, в его центре
на перпендикуляре к оси диполя, в его центре 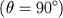
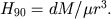
Реальные магнитные тела можно рассматривать как совокупность элементарных магнитных диполей.
Интенсивность намагничения элементарного объема ( 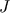 ), согласно определению, равна отношению магнитного момента (
), согласно определению, равна отношению магнитного момента ( 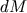 ) к его объему (
) к его объему ( 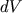 ). Поэтому выражение для потенциала магнитного диполя перепишется в следующем виде:
). Поэтому выражение для потенциала магнитного диполя перепишется в следующем виде: 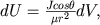 где вектор
где вектор 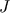 направлен вдоль оси диполя.
направлен вдоль оси диполя.
Mагнитный потенциал любого тела можно представить в виде интеграла по объему этого тела от потенциалов элементарных диполей, из которых состоит данное тело:
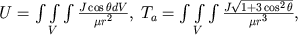
| (2.6) |
где интегрирование ведут по всему объему тела ( 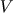 ).
).
Эти уравнения лежат в основе всей теории магниторазведки. Аналитические выражения при решении уравнений (2.6) получаются лишь для тел простой геометрической формы и однородной (постоянной) намагниченности. Для тел более сложной формы, да еще при разной намагниченности, возможны численные решения с помощью ЭВМ. Рассмотрим решение прямых и обратных задач для некоторых простейших тел: вертикального бесконечного столба (стержня), шара, пласта и горизонтального цилиндра бесконечного простирания для случая их вертикальной намагниченности. Допущение вертикальной намагниченности не только упрощает решение задач, но и является вполне обоснованным, поскольку намагниченность горных пород при широте, большей 40 - 45  , близка к вертикальной. Кроме того, при расчетах можно считать, что
, близка к вертикальной. Кроме того, при расчетах можно считать, что 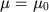 , где
, где 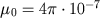 - магнитная проницаемость воздуха.
- магнитная проницаемость воздуха.
Дата добавления: 2021-05-28; просмотров: 487;











