Прямая и обратная задачи над вертикально намагниченным тонким пластом бесконечного простирания и глубины.

Пусть на глубине 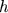параллельно оси y расположен бесконечно длинный вертикальный пласт (с толщиной 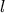, меньшей глубины залегания), намагниченный вертикально (рис. 2.6). Определим для простоты лишь 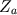вдоль оси .

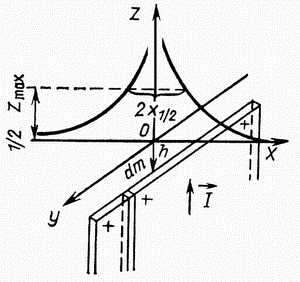
Рис. 2.6. Магнитное поле тонкого пласта бесконечного простирания

Поскольку нижняя часть пласта расположена глубоко, то влияние магнитного полюса глубоких частей пласта будет мало, и можно считать, что магнитные массы сосредоточены вдоль поверхности в виде линейных полюсов. Магнитная масса единицы длины пласта равна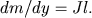

Разобьем пласт на множество тонких "столбов". Тогда притяжение пласта будет складываться из притяжения всех элементарных столбов, а вертикальная составляющая его магнитного притяжения будет равна интегралу в пределах от 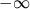до (по оси ) выражения для притяжения элементарного столба. Потенциал элементарного тонкого столба равен

,

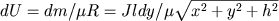
а вертикальная составляющая ,

откуда 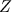равно

(2.13)

График 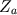будет иметь максимум над центром пласта и асимптотически стремиться к нулю при удалении от пласта. В плане над пластом будут вытянутые аномалии 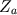одного знака. Анализируя формулу (2.13), можно найти связи между глубиной залегания пласта ( 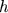) и 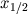, т.е. абсциссой графика, где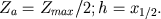

Магнитная масса единицы длины равна . Заменив 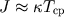, получим 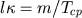. Зная и , можно рассчитать ширину пласта.