Множественная корреляция.

Выше рассматривалась зависимость между двумя признаками, т.е. речь шла о так называемой “парной” корреляции.

На практике чаще всего изменение изучаемого признака зависит от действия нескольких причин. В таких случаях изучение корреляционной связи не может ограничиваться парными зависимостями, и в анализ необходимо включить другие признаки-факторы, существенно влияющие на изучаемый результативный признак. Одновременное изучение корреляции нескольких переменных проводится на основе использования методов множественной корреляции. При этом осуществляется оценка влияния каждого из факторов на результативный признак, построение уравнения множественной регрессии и определение его параметров.

В случае линейной связи между m факторами-признаками и результативным признаком зависимость может быть представлена линейным уравнением множеcтвенной регрессии:

.

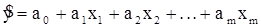Обозначим номер наблюдения: i=1, 2, 3, ..., n, номер независимой переменной: j=1, 2, 3, ..., m.

Параметры уравнения регрессии определяются методом наименьших квадратов.

В случае линейного уравнения регрессии ее параметры определяются следующим образом:

,

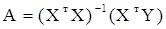где А - вектор-столбец оценок параметров:

;

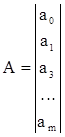X - матрица значений независимых переменных (факторов) размерностью n(m+1):

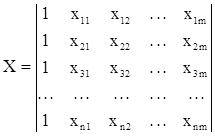
Y - вектор-столбец значений зависимой переменной (результативного признака):

.

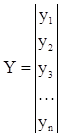По параметрам полученного уравнения можно оценить долю каждого из факторов в изменении уровня результативного признака. то может быть сделано путем прямой оценки по величине коэффициентов регрессии при каждом из факторов, а также по коэффициентам эластичности, совокупным и частным коэффициентам регрессии, b - коэффициентам и D - коэффициентам.

Коэффициенты уравнения множественной регрессии показывают абсолютный размер влияния факторов на уровень результативного показателя и характеризуют степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) уровне других факторов, входящих в модель.

Для сравнения оценок роли различных факторов в формировании моделируемого показателя следует абсолютные величины дополнить относительными.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменяется результативный признак у с изменением признака-фактора x_j на один процент при фиксированном положении других факторов, и рассчитываются по формуле:

,

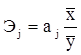где а_j - коэффициент регрессии при j-м факторе.

b - коэффициенты показывают, на какую часть среднего квадратического отклонения s_у изменится зависимая переменная у с изменением соответствующего фактора х_j на величину своего среднеквадратического отклонения s_х. Этот показатель позволяет сравнивать влияние колеблемости различных факторов на вариацию исследуемого показателя, на основе чего выявляются факторы, в развитии которых заложены наибольшие резервы изменения результативного показателя:

.

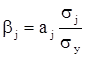Коэффициенты эластичности и b - коэффициенты связаны следующим образом:

,

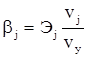где v_j - коэффициент вариации j-го факторного признака;

v_y - коэффициент вариации результативного признака.

Чтобы оценить долю влияния каждого фактора в суммарном влиянии факторов, включенных в уравнение регрессии, рассчитывают D - коэффициенты:

,

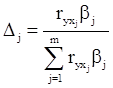где 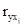- парные коэффициенты корреляции.

Величина совокупного коэффициента корреляции для случая зависимости результативного признака от двух факторных признаков может быть определена следующим образом:

.

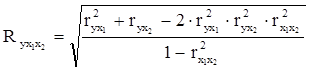Величина совокупного коэффициента корреляции изменяется в пределах от 0 до 1 и численно не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе совокупный коэффициент корреляции к единице, тем меньше роль неучтенных в модели факторов.

Для более глубокого исследования связей между явлениями целесообразно установить степень тесноты связи между результативным признаком у и каждым из факторных признаков при исключении влияния других факторных признаков.

Для решения поставленной задачи определяют частные коэффициенты корреляции.

Для случая зависимости у от двух факторов можно вычислить два коэффициента частной корреляции:

;

.

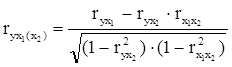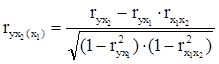Построение многофакторных регрессионных моделей позволяет дать количественное описание основных закономерностей изучаемых явлений, выделить существенные факторы, обуславливающие изменение экономических показателей, и оценить их влияние.

В основном полученные модели используются в двух направлениях - для сравнительного анализа и в прогнозировании.