Между двумя признаками.

После установления факта наличия связи и ее формы измеряется степень тесноты связи и проводится оценка ее существенности.

Зная показатели тесноты корреляционной связи можно решить следующие группы вопросов:

ответить на вопрос о необходимости изучения данной связи между признаками и целесообразности ее практического применения;

сопоставляя показатели тесноты связи для различных ситуаций, можно судить о степени различий в ее проявлении для конкретных условий;

сопоставляя показатели тесноты связи результативного признака с различными факторами, можно выявить те факторы, которые в данных конкретных условиях являются решающими, и главным образом воздействуют на формирование величины результативного признака.

К простейшим показателям степени тесноты связи относят коэффициент корреляции знаков (коэффициент Г. Фехнера). Для расчета этого показателя вычисляют средние значения факторного и результативного признаков, а затем проставляют знаки отклонений для всех значений взаимосвязанных пар признаков.

Коэффициент Г. Фехнера определяется по формуле:

,

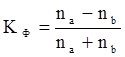где n_a - число совпадений знаков отклонений индивидуальных величин от средней;

n_b - число несовпадений знаков отклонений.

Коэффициент Фехнера может принимать различные значения в пределах от -1 до +1. Если К_Ф по модулю приближается к единице, то это свидетельствует о возможном наличии связи между явлениями. Знак коэффициента определяет направление этой связи.

№	x	y	Знак отклонений	Совпадение - а,
			для х	для у	несовпадение - b
	96.7		-	-	a
	97.0		-	-	a
	98.0		-	-	a
	98.5		-	-	a
	100.0		-	-	a
	100.0		-	-	a
	100.6		-	-	a
	100.7		-	-	a
	100.8		-	-	a
	101.0		-	-	a
	101.2		-	-	a
	101.8		-	-	a
	102.3		-	-	a
	103.0		-	-	a
	103.0		-	+	b
	103.1		-	-	a
	103.7		+	-	b
	104.3		+	-	b
	105.2		+	+	a
	105.3		+	+	a
	105.8		+	+	a
	106.8		+	+	a
	106.4		+	+	a
	106.9		+	+	a
	107.0		+	+	a
	107.0		+	+	a
	108.0		+	+	a
	108.3		+	+	a
	110.0		+	+	a
	112.0		+	+	a
Итого	3103.6

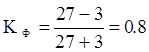
Поскольку величина коэффициента зависит только от знаков отклонений величин факторного и результативного признака от соответствующих средних, и не зависит от величины этих отклонений, то с помощью данного показателя нельзя определить степень тесноты связи. Коэффициент Фехнера отвечает на вопрос о наличии и направлении корреляционной связи между явлениями. В том случае, если построена корреляционная или групповая таблица, дополнительный расчет коэффициента Фехнера не имеет практической ценности.

Линейный коэффициент корреляции является более совершенным показателем степени тесноты связи. При расчете этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сами величины этих отклонений:

;

.

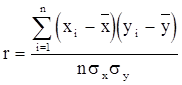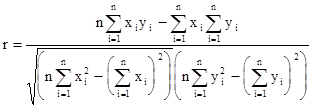Расчет линейного коэффициента корреляции по корреляционной таблице производится по формуле:

.

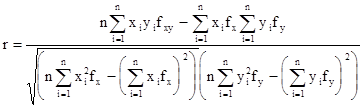Линейный коэффициент корреляции может принимать любые значения в пределах от -1 до +1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками.

Квадрат коэффициента корреляции (R=r²) носит название коэффициента детерминации.

Коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае наличия линейной зависимости между признаками. При наличии же криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен нулю, поэтому в таких случаях рекомендуется использовать в качестве показателя степени тесноты связи эмпирическое корреляционное отношение h.

,

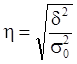где 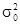- общая дисперсия результативного признака;

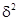- межгрупповая дисперсия результативного признака.