Общие подходы к решению прямых задач электроразведки.
В основе теории электроразведки лежат уравнения Максвелла, являющиеся постулатами макроскопической электродинамики. Они включают в себя все основные законы электромагнетизма (законы Ома, Ампера, Кирхгофа и др.) и описывают поля в разных средах. Из уравнений Максвелла получается дифференциальное уравнение, названное телеграфным. Решая его, можно получить электрическую (  ) компоненту поля в средах вдали от источника с электромагнитными параметрами
) компоненту поля в средах вдали от источника с электромагнитными параметрами 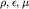 :
:
 , где , где 
| (3.5) |
Дифференцирование ведется по декартовым координатам ( х, у, z) и времени (  ). Уравнение для магнитной (
). Уравнение для магнитной (  ) компоненты поля аналогично.
) компоненты поля аналогично.
Если геоэлектрический разрез известен, то с помощью уравнения (3.5) и физических условий задачи, называемых условиями сопряжения, решаются прямые задачи электроразведки, т.е. получаются аналитические или численные значения  и
и  , которые соответствуют заданному геоэлектрическому разрезу. В теории электроразведки прямые задачи решаются для разных физико-геологических моделей (ФГМ) сред. Под ФГМ понимаются абстрактные геоэлектрические разрезы простой геометрической формы, которыми аппроксимируются реальные геолого-геофизические разрезы. Сложность решения прямых задач заключается в выборе моделей, близких к реальным, но таких, чтобы для избранного типа первичного поля удалось получить хотя бы приближенное решение для
, которые соответствуют заданному геоэлектрическому разрезу. В теории электроразведки прямые задачи решаются для разных физико-геологических моделей (ФГМ) сред. Под ФГМ понимаются абстрактные геоэлектрические разрезы простой геометрической формы, которыми аппроксимируются реальные геолого-геофизические разрезы. Сложность решения прямых задач заключается в выборе моделей, близких к реальным, но таких, чтобы для избранного типа первичного поля удалось получить хотя бы приближенное решение для  или
или  . Для этого применяется математическое моделирование с использованием современных ЭВМ. В недалеком прошлом основным способом решения прямых задач для сложных ФГМ и разных по структуре типов полей являлось физическое моделирование на объемных или плоскостных моделях сред.
. Для этого применяется математическое моделирование с использованием современных ЭВМ. В недалеком прошлом основным способом решения прямых задач для сложных ФГМ и разных по структуре типов полей являлось физическое моделирование на объемных или плоскостных моделях сред.
Наиболее простыми моделями сред являются:
однородное изотропное пространство или полупространство с одинаковыми электромагнитными свойствами (решения над ними называются соответственно первичным или нормальным полем источника);
анизотропное пространство или полупространство с электромагнитными свойствами, отличающимися в направлении и вкрест слоистости пород;
одномерные неоднородные среды, в которых свойства меняются в одном направлении. Такими ФГМ могут быть, например, вертикальные контакты двух сред, ряд вертикальных пластов или горизонтально слоистая среда с разными  ;
;
двухмерные неоднородные среды, в которых электромагнитные свойства меняются в двух направлениях. Примером могут быть наклонные пласты или цилиндры, простирающиеся вдоль одного направления и отличающиеся по  от вмещающих горных пород;
от вмещающих горных пород;
трехмерные неоднородные среды, в которых свойства меняются по трем направлениям. Самой простой из подобных моделей является шар с разными  или
или  в однородном полупространстве.
в однородном полупространстве.
В порядке увеличения сложности структуры первичных полей, а значит возрастания сложности решения прямых задач, используемые для электроразведки поля можно расположить в следующей последовательности: точечных и дипольных источников постоянного тока, плоских гармонических электромагнитных волн, сферических волн дипольных гармонических или импульсных источников, цилиндрических волн длинного кабеля и т.п.
Существуют различные подходы к решению прямых задач с помощью уравнения (3.5). Любое правильное решение, удовлетворяющее всем физическим требованиям, единственно и корректно. Под корректностью понимается такое решение, в котором малым изменениям исходных данных соответствуют малые приращения расчетных параметров.
7.3.2. О нормальных полях в электроразведке.
Как отмечалось выше, под нормальным полeм понимается электромагнитное поле того или иного источника над однородным изотропным полупространством с неизменными электромагнитными свойствами.
Из простейшей прямой задачи о поле точечного источника постоянного тока на земной поверхности (см. 7.1.3) можно получить нормальные поля постоянных электрических токов для разных установок или разных комбинаций питающих ( АВ) и приемных ( МN) электродов (см. рис. 3.2).
В практике электроразведки часто применяются четырехэлектродные установки АМNВ (см. рис. 3.2).

|
| Рис. 3.2. План расположения питающих (А и В) и приемных ( М и N) электродов в разных установках метода сопротивлений: а - четырехэлектродной, б - срединного градиента, в - симметричной четырехэлектродной, г - трехэлектродной, д - двухэлектродной, е - дипольной радиальной, ж - дипольной азимутальной |
К одному питающему электроду (например, А) подключается положительный полюс источника тока, к другому ( В) - отрицательный. Разность потенциалов на приемных электродах ( МN) от электрода А, определенная по полученной выше формуле (3.1), равна:
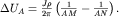
|
Аналогичным образом можно получить разность потенциалов от отрицательного полюса В, но величину тока следует принять равной ( 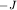 ).
).
Разность потенциалов от обоих электродов АВ равна суперпозиции  и
и 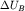 :
:
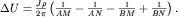
| (3.6) |
Если МN установить в центре АВ так, чтобы АМ = BN, АN = ВМ, то получим формулу для расчета  симметричной четырехэлектродной установки (см. рис. 3.2):
симметричной четырехэлектродной установки (см. рис. 3.2):
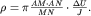
| (3.7) |
Потенциал двухэлектродной установки АМ ( А и N удалены в бесконечность) можно получить из (3.6), приняв 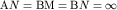 , т.е.
, т.е.  .
.
В методах сопротивлений применяется и ряд других установок. Так, например, для глубинных исследований используются различные дипольные установки (рис. 3.2). Если приемный диполь ( МN) перпендикулярен радиусу (  ) между его центром и центром питающего диполя ( АВ), а угол между радиусом и питающей линией АВ (
) между его центром и центром питающего диполя ( АВ), а угол между радиусом и питающей линией АВ (  ) находится в пределах
) находится в пределах  , то такая установка называется азимутальной. Частным случаем азимутальной является экваториальная установка (
, то такая установка называется азимутальной. Частным случаем азимутальной является экваториальная установка ( 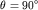 ). Если приемный диполь (МN) направлен вдоль
). Если приемный диполь (МN) направлен вдоль  , а
, а 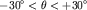 , то такая установка называется радиальной. Частным случаем радиальной установки является осевая (
, то такая установка называется радиальной. Частным случаем радиальной установки является осевая ( 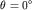 ).
).
Для каждой установки можно получить формулы, по которым рассчитывается коэффициент установки. Так, для азимутальной установки 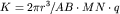 , для радиальной
, для радиальной 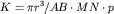 , где
, где  и
и  - коэффициенты, мало отличающиеся от единицы и определяемые по специальным номограммам.
- коэффициенты, мало отличающиеся от единицы и определяемые по специальным номограммам.
Таким образом, при работах любой установкой  рассчитывается по формуле для нормального поля
рассчитывается по формуле для нормального поля
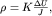
| (3.8) |
где 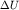 - разность потенциалов на МN,
- разность потенциалов на МN, 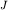 - ток в АВ, а
- ток в АВ, а 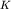 - коэффициент устaновки, зависящий лишь от расстояний между электродами.
- коэффициент устaновки, зависящий лишь от расстояний между электродами.
Как отмечалось выше, по этим же формулам можно рассчитать некоторое \rho над реальным, неизвестным и практически всегда неоднородным полупространством. Тогда оно называется кажущимся (КС или 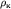 ).
).
Расчет нормальных полей для других источников (гармонических, импульсных) очень сложен, но в любом случае принято получать КС (см. 7.1.3 - 7.1.5).
7.3.3. Электрическое поле точечного источника постоянного тока над двухслойной средой.
Простейшей, но очень важной для практики электроразведки методом сопротивлений, одномерной прямой задачей является задача об электрическом поле и кажущемся сопротивлении на поверхности полупространства, верхнее из которых воздух, а нижнее - двухслойная горизонтально слоистая среда с мощностью верхнего слоя 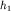 , нижнего
, нижнего 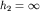 , УЭС слоев
, УЭС слоев 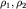 и
и 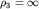 (воздух) (см. рис. 3.3).
(воздух) (см. рис. 3.3).
Поставленная задача могла бы быть решена с помощью уравнения (3.2), которое при 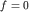 превращается в уравнение Лапласа
превращается в уравнение Лапласа  , где
, где 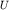 - потенциал в любой точке М с напряженностью электрического поля
- потенциал в любой точке М с напряженностью электрического поля 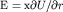 .
.
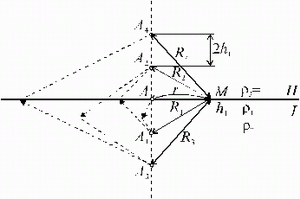
|
| Рис.. 3.3. Решение прямой задачи о поле точечного источника постоянного тока над двухслойной средой методом зеркальных отражений |
Однако ее можно быстро решить методом зеркальных отражений. Согласно правилам метода зеркальных отражений, урав-нение Лапласа и физические требования, в том числе граничные условия, выполняются, если потенциал в одномерной среде, где расположен точечный источник, принять равным сумме потенциалов этого источника (  ) и всех его многократных отражений от границ раздела (
) и всех его многократных отражений от границ раздела ( 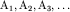 ) с коэффициентами отражений, равными на границе I
) с коэффициентами отражений, равными на границе I 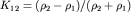 , а на границе II
, а на границе II  (т.к.
(т.к. 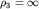 ).
).
На рис. 3.3 показано, как эти источники расположены. При этом обозначено

|
где  .
.
Таким образом, искомое выражение для потенциала получает вид:
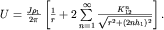
| (3.9) |
Выражение для КС (3.1) можно записать в виде: 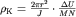 , где
, где 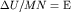 - напряженность электрического поля. Но
- напряженность электрического поля. Но 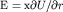 , поэтому
, поэтому  . Подставив в эту формулу производную
. Подставив в эту формулу производную 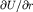 из (3.9), получим
из (3.9), получим

|
Откуда
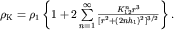
| (3.10) |
Анализируя эту формулу, можно найти асимптотические выражения 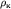 , равные
, равные 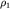 и
и 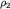 . В самом деле, при
. В самом деле, при 
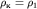 , при
, при 

|
(т.к. 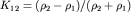 , а
, а 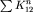 равна
равна 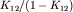 как сумма членов геометрической прогрессии).
как сумма членов геометрической прогрессии).
С помощью формулы (3.10), справедливой для трехэлектродной и симметричной четырехэлектродной градиент-установок, принято строить теоретические двухслойные кривые - графики зависимости  ) от
) от  . Они называются двухслойными теоретическими кривыми ВЭЗ (вертикальное электрическое зондирование) (см. 8.2), или двухслойной палеткой ВЭЗ (см. рис. 3.4).
. Они называются двухслойными теоретическими кривыми ВЭЗ (вертикальное электрическое зондирование) (см. 8.2), или двухслойной палеткой ВЭЗ (см. рис. 3.4).

|
| Рис. 3.4. Двухслойная палетка ВЭЗ: 1 и 2 - теоретические и полевая кривые |
Более громоздкое решение получается в задаче о поле точечного источника над многослойной горизонтально слоистой средой, а еще сложнее решение для такой же среды, но при возбуждении поля дипольными гармоническими или импульсными источниками.
Одномерные прямые задачи электроразведки для многослойных горизонтально слоистых сред для любых первичных полей все-таки сводятся к аналитическим формулам для расчета КС. В результате принято строить кривые КС, аналогичные приведенным на рис. 3.4.
Двухмерные и трехмерные прямые задачи электроразведки сводятся к аналитическим формулам лишь для тел простой формы (шар, пласт, цилиндр) в однородной среде. В более общих случаях получаются лишь приближенные численные решения, получаемые с помощью ЭВМ.
7.3.4. Принципы решения обратных задач электроразведки.
Накопленный материал по физическому и математическому моделированию прямых задач электроразведки привел к созданию методов решения обратных задач, т.е. определению тех или иных параметров геоэлектрического разреза по наблюденным графикам  ,
,  или, например, кривым КС. Решение обратных задач неоднозначно в силу его некорректности, как и всех обратных задач математической физики. Некорректность проявляется в том, что малым изменениям наблюденных параметров поля могут соответствовать большие изменения параметров разреза. Этот физический факт получил название принципа эквивалентности. Принципом эквивалентности объясняется, например, невозможность точного определения мощностей (
или, например, кривым КС. Решение обратных задач неоднозначно в силу его некорректности, как и всех обратных задач математической физики. Некорректность проявляется в том, что малым изменениям наблюденных параметров поля могут соответствовать большие изменения параметров разреза. Этот физический факт получил название принципа эквивалентности. Принципом эквивалентности объясняется, например, невозможность точного определения мощностей ( 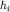 ) и удельных электрических сопротивлений (
) и удельных электрических сопротивлений (  ) тонких слоев, горизонтально слоистого разреза, хотя такие параметры, как продольные проводимости (
) тонких слоев, горизонтально слоистого разреза, хотя такие параметры, как продольные проводимости ( 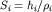 ) либо поперечные сопротивления (
) либо поперечные сопротивления (  ), в определенных разрезах расcчитываются однозначно (см. 9.1).
), в определенных разрезах расcчитываются однозначно (см. 9.1).
Методы решения обратных задач электроразведки являются основой количественной интерпретации данных электроразведки (см. 9). Сущность их сводится к подбору и сравнению полевых графиков и кривых с теоретическими, полученными в результате решения прямых задач. Для этого созданы альбомы типичных теоретических кривых (палетки) или программы для их теоретического расчета с помощью ЭВМ (см. 9.1).
8. Аппаратура, методика и сущность разных методов электроразведки
8.1. Принципы устройства и назначение аппаратуры для электроразведки
Из-за наличия множества методов электроразведки используются или создаются специально разнообразные комплекты аппаратуры и оборудования. Создаваемые и выпускаемые малосерийные приборы быстро устаревают и непрерывно совершенствуются в направлении увеличения числа одновременно регистрирующих каналов, компьютеризации измерений и обработки информации. Поэтому остановимся лишь на принципах устройства и назначения основных групп приборов. Для изучения небольших глубин (до 500 м) используются переносные приборы и оборудование. Разведка больших глубин (свыше 0,5 км) осуществляется с помощью электроразведочных станций (ЭРС). Ускоренное геологическое картирование и поиск полезных ископаемых на глубинах до 200 м выполняется с помощью аэроэлектроразведочных станций.
Дата добавления: 2021-05-28; просмотров: 548;











