Примеры применения интегральной теоремы Муавра-Лапласа

Пример. Выборочная проверка показала, что из 100 изделий 87 удовлетворяют стандарту. Мы хотим быть уверены на 95%, что не ошибаемся в оценке процента не стандарта. В каких пределах он находится? Каков должен быть объем выборки, чтобы оценить процент брака с точностью до 0,01?

Решение. По теореме Муавра-Лапласа с вероятностью 0,95

.

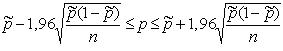Подставляя в эту формулу наши данные – n = 100 и 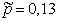, получаем, что 0,06 < p < 0,2. Для нахождения объема выборки N, необходимого для получения оценки p с точностью до 0,01, то же неравенство выписываем в следующей форме: 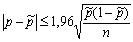. Откуда

.

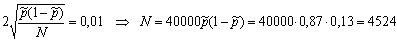Следовательно, чтобы определить процент “брака” с точностью до 0,01 и гарантией 0,95, необходимо провести выборочную проверку не менее, чем для 4524 изделий.

Пример. Страховая компания страхует n домов на 10000 рублей каждый. Вероятность того, что застрахованный дом сгорит за год, равна p = 0,01. Найти K такое, что P{mK} = 0,025, где m - число сгоревших за год домов. Найти величину выплат S, рассчитанных на то, что сгорит K домов, и сумму s, которую надо брать с каждого дома, чтобы обеспечить такие выплаты (тогда в среднем только раз в 40 лет компания не уложится в собранную сумму и вынуждена будет взять деньги из собственных фондов или прибегнуть к займу). Сравнить суммы, которые надо брать со страхуемого дома для n=1000000, n=10000, n=1000.

Решение. Согласно интегральной теореме Муавра-Лапласа

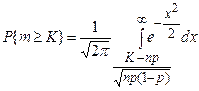и находим из таблиц, что

.

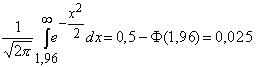Следовательно, .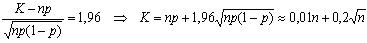

Для выплат надо собрать S(n)=10000(0,01n+0,2 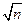)=100n+2000 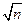рублей, с одного дома s(n)=100+2000 / 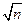рублей.

Ответ:

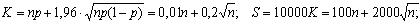
s(1000000) = 102 руб., s(10000) = 120 руб., s(1000) = 160 руб.

Итак, если ваша фирма имеет 1000 клиентов, то в качестве страхового взноса за дом стоимостью 1000 руб. надо брать 160 руб., если у вас 10000 клиентов – то 120 руб., если 1000000 – всего 102 руб. Тогда с вероятностью 0,975 вам при выплате страховки достаточно будет собранных средств (примерно 2-3 раза в 100 лет вам этой суммы не хватит и придется прибегнуть к займу в ожидании более счастливого года, когда пожаров будет меньше).

Пример. Нормативная грузоподъёмность железнодорожной цистерны равна 60 тонн. Считая загрузку каждой цистерны нормально распределённой случайной величиной с математическим ожиданием, равным 60 тонн, со среднеквадратическим отклонением s = 2 т (зависит от точности работы загрузочного устройства), необходимо найти закон распределения, математическое ожидание и среднеквадратическое отклонение грузоподъёмности состава из 50 цистерн.

Решение. Рассматривая грузоподъёмность состава как случайную величину z = x₁+ ... + x₅₀, равную сумме грузоподъёмностей всех цистерн, на основании свойства устойчивости нормального распределения можем утверждать, что z также распределена нормально с числовыми характеристиками:

= .

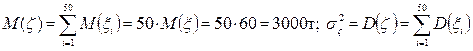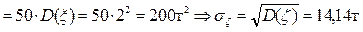Теперь, зная распределение веса, загруженного в состав, решим “обратную задачу”: в каких пределах с вероятностью 0,997 находится загруженный в состав вес? А в каких пределах он находится с вероятностью 0,954?

Воспользуемся полученным значением s и правилом 3s и 2s, согласно которому с вероятностью 0,9973 грузоподъёмность состава не выйдет за пределы интервала (3000 - 3×14,14; 3000 + 3×14,14), то есть (2957,58; 3042,42), а с вероятностью 0,954 вес состава не выйдет за пределы интервала (3000-2×14,14; 3000+2×14,14), то есть (2972; 3028).

Полученные ответы показывают, что за большую уверенность мы платим расширением интервала.