Характеристические функции (Термодинамические потенциалы)

По прежнему рассматриваем простейшую систему с одним внешним параметром. Основное уравнение:

TdS = dU + pdV (1)

Здесь, однако, 5 переменных. Само же состояние системы описывается двумя, например, Т и V, а остальные 3 функции неизвестны. Для их определения надо добавить еще уравнение состояния p = p(V, T) (2) и зависимость U = U(V,T) (3) (для идеального газа – закон Джоуля U = C_VT). Однако, если правильно выбрать независимые переменные вместо двух дополнительных уравнений можно обойтись и одним. Например, пусть знаем U = U(S, V), Перепишем (1) как

dU = TdS – pdV (4)

Выберем S и V как независимые переменные. U – полный дифференциал.

Тогда

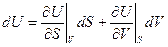, т.е. 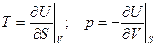(5)

Эти формулы аналогичны по структуре формулам, связывающим в механике силу и потенциальную энергию. Поэтому внутренняя энергия U называется термодинамическим потенциалом (характеристическая функция в переменных U и V). Метод термодинамических потенциалов (мы увидим, что не один) был развит Гиббсом во второй половин 19 века. Из равенства смешанных производных следует:

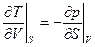(6)

Это соотношение взаимности (первое) Максвелла, связывающее два свойства системы: изменение температуры при адиабатическом расширении и изменение давление при изохорном сообщении теплоты системе. Установление таких связей и составляет метод термодинамических потенциалов.

Еще: 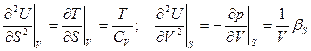Можно найти C_V и β_S

Возьмем другие переменные: T и V. Перепишем (1) в виде:

TdS + SdT – SdT = dU + pdV, или d(U-ST) = -pdV – SdT (7)

Здесь F = U – TS (8) – свободная энергия термодинамическая функция в переменных V и T:

dF = -pdV – SdT (7`)

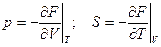(9)

Соотношение взаимности здесь: 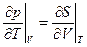(10)

(еще называют функцией Гельмгольца)

Почему свободная энергия? Из (7`) следует, что при изотермических процессах работа совершается только за счет убыли F, а не U (как при адиабатических процессах), т.е.F характеризует возможность системы совершать работу. Величина TS называется связной энергией. В ТД внутренняя энергия складывается из свободной и связной: U = F + TS (в механике кинетической и потенциальной)

Еще: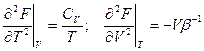

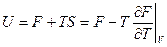(11) – 1-е уравнение Гиббса-Гельмгольца, связывающее U и F

Возьмем независимые переменные p и T.

(7`): dF = -SdT – pdV +Vdp – pdV = -SdT + Vdp – d(pV) => dФ = d(F + pV) = -SdT +Vdp (12)

Ф = F + pV = U – TS + pV (12`) – энергия Гиббса (термодинамический потенциал Гиббса)

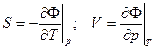(13)

Соотношение взаимности Максвелла

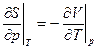(14)

Используя Ф, удобно получить выражение для С_p (вторая производная t):

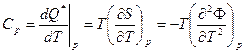(15)

Другая вторая производная дает коэффициент сжимаемости:

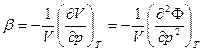(16)

Физический смысл: при изотермическом процессе (dT = 0) убыль энергии Гиббса
(-Vdp) равна работе расширения системы (газ + поршень с грузом) при адиабатических процессах!!!

Энергия такой системы равна:

E = U + pSh

dE = dU + pdV +Vdp; и при dS = 0:

-dE = -Vdp (убыль энергии равна работе) Другой смысл Ф – убыль Ф = работе немеханических сил, но это в более сложных системах, можно показать.

Еще про Ф: (12`)

U = Ф + TS – pV. С учетом (13):

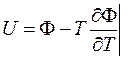U = Ф -

Наконец возьмем независимые переменные S и P

Тогда (вперед!)

dU = TdS – pdV ± Vdp = TdS +Vdp – d(pV)

dI = d(U + pV) = TdS + Vdp (18)

I = U + pV – теплосодержащая функция или энтальпия.

При p = const => đQ^* = dI, кроме того I = E – энергии расширенной системы

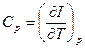(19)

из (18)

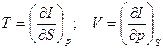(19`)

Соотношение взаимности:

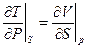(20)

устанавливает связь между термодинамическими потенциалами и позволяет решить ряд практических задач. НО!!! Сами потенциалы должны быть определены из опыта (например, идеальный газ U = C_VT) или вычислен с помощью статфизики. Статфизикой займемся уже на следующей лекции. А пока соотношение взаимности получили в простой системе с одним внешним параметром V. Что в более сложных системах?

Основное уравнение:

(21) 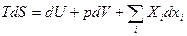, где x_i – внешние параметры (остальные)

Отсюда: 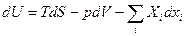; и если за независимые переменные взять набор {S, V, x_i}, то характеристическая функция – внутренняя энергия.

Если {T, V, x_i}, то характеристическая функция – свободная энергия.

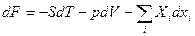(22)

Если {T, p, X_i} (обобщенные силы взяты за независимые переменные), то характеристическая функция – потенциал Гиббса 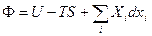(23)

И наконец {T, S, X_i}, то – энтальпия I = U + pV +X_ix_i, и:

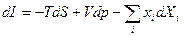(24)

Однако, можно выбрать, например, {T, p, X_i} или {T, S, x_i}, тогда выражения для Ф и I останутся как раньше: Ф = U - TS + pV, I = U pV, а в (21) и (22) 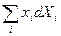заменить на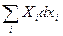

Можно вводить и новые характеристические функции добавляя в (22, например) 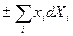, тогда 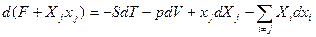, и F+X_jx_j. – новая характеристическая функция. Все это – основы термодинамического аппарата.

Пример применения: Газ Ван-дер-Ваальса. 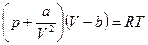(1), здесь a и b – константы Ван-дер-Ваальса:

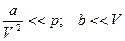. b – объем молекул, а 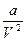- внутренняя энергия газа, определяемая взаимным притяжением молекул газа. Из (1): 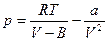. Подставляем в 1-е следствие основного уравнения:

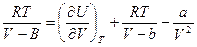и 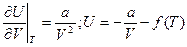Отсюда, при Và∞ U = f(T), но при Và∞ переход к идеальному газу, где U = C_VT. Следовательно f(T) = 0 и U = C_VT – a/V