Линейные дифференциальные уравнения второго порядка
Определение 4. Линейным дифференциальным уравнением второго порядка называется уравнение вида:
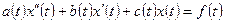 , (3.16)
, (3.16)
где 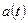 ,
, 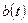 ,
, 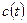 и
и 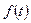 - заданные функции, причем
- заданные функции, причем 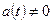 . Здесь, для удобства записи использованы обозначения
. Здесь, для удобства записи использованы обозначения 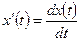 ,
, 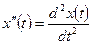 .
.
Если функции 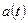 ,
, 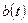 ,
, 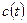 постоянны, то уравнение (3.16) называют уравнением с постоянными коэффициентами.
постоянны, то уравнение (3.16) называют уравнением с постоянными коэффициентами.
Если 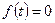 при всех значениях
при всех значениях 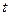 , то уравнение называют однородным.
, то уравнение называют однородным.
Рассмотрим однородное уравнение с постоянными коэффициентами:
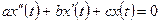 , (3.17)
, (3.17)
где 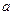 ,
, 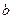 ,
, 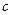 - постоянные, причем
- постоянные, причем 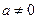 .
.
Решение уравнения (3.17) будем искать в виде:
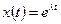 ,
,
где 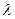 - некоторое число.
- некоторое число.
Учитывая, что 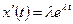 ,
, 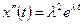 из (3.17) имеем:
из (3.17) имеем:
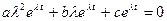 .
.
Или
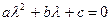 . (3.18)
. (3.18)
Уравнение (3.18) называется характеристическим уравнением для уравнения(3.17). Корнями характеристического уравнения служат
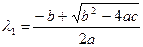 ,
, 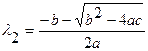 . (3.19)
. (3.19)
Нужно рассмотреть три случая: величина 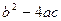 больше нуля, равна нулю или меньше нуля.
больше нуля, равна нулю или меньше нуля.
Случай 1. Пусть 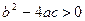 , т.е.
, т.е. 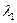 и
и 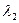 действительны и различны. Тогда дифференциальное уравнение имеет два разных решения:
действительны и различны. Тогда дифференциальное уравнение имеет два разных решения: 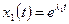 и
и 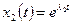 . Общее решение записывается в виде:
. Общее решение записывается в виде:
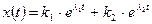 , (3.20)
, (3.20)
где 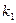 и
и 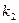 - произвольные постоянные. Чтобы найти
- произвольные постоянные. Чтобы найти 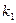 и
и 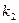 нужно знать два условия, которым должно удовлетворять решение
нужно знать два условия, которым должно удовлетворять решение 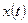 , например,
, например, 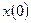 и
и 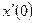 .
.
Случай 2. Пусть 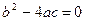 . В этом случае корни характеристического уравнения равны между собой:
. В этом случае корни характеристического уравнения равны между собой: 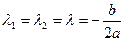 . Одним решением (3.17) является функция
. Одним решением (3.17) является функция 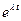 , а другим
, а другим 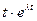 . Общее решение имеет вид:
. Общее решение имеет вид:
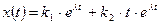 . (3.21)
. (3.21)
Случай 3. Пусть 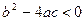 . В этом случае корни характеристического уравнения (3.18) представляют собой комплексно-сопряженные числа
. В этом случае корни характеристического уравнения (3.18) представляют собой комплексно-сопряженные числа
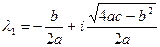 и
и 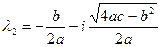 .
.
Общее решение уравнения (3.17 запишется в виде:
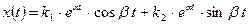 , (3.22)
, (3.22)
где 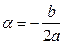 ,
, 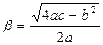 .
.
Пример 9. В благоприятных условиях выращивают две популяции мух. Для популяции I удельная скорость роста составляет 0.1, если время выражается в днях. Для популяции II аналогичная скорость составляет 0.08. Определим 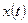 как суммарную численность двух популяций в момент
как суммарную численность двух популяций в момент 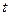 . Найти дифференциальное уравнение второго порядка, которому удовлетворяет
. Найти дифференциальное уравнение второго порядка, которому удовлетворяет 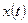 .
.
Решение: По условию задачи 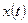 - суммарная численность двух популяций мух. Учитывая, что
- суммарная численность двух популяций мух. Учитывая, что 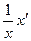 - есть удельная скорость роста, то для
- есть удельная скорость роста, то для 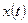 имеем уравнение
имеем уравнение
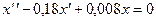 .
.
Это есть дифференциальное уравнение второго порядка, которому удовлетворяет 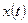 . Решая, находим:
. Решая, находим:
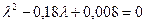 .
.
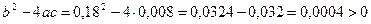 .
.
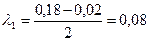 ;
; 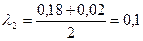 .
.
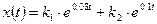 - общее решение уравнения.
- общее решение уравнения.
Дата добавления: 2017-01-08; просмотров: 1056;










