СТРУКТУРА ПОТОКА И ПОПЕРЕЧНЫЙ ПЕРЕНОС

Начнем с упрощенной схемы. Пред­ставим себе дорогу, идущую под уклон. При этом вся дорога состоит из серии параллельных неглубоких желобков. По желобкам катятся шарики. По бокам дороги — крутые стенки, так что шарики вылететь с нее не могут. Пока уклон невелик, невелика и скорость, и каж­дый шарик катится по «своему» желоб­ку. Все они движутся параллельно друг другу. Эта картина соответствует тече­нию жидкости при малых скоростях: каждая частица жидкости движется па­раллельно другим. При этом обнаружи­вается одна особенность, которую не мо­жет передать наша модель «шарики в желобках». Непосредственно у стенки скорость жидкости равна нулю. Жид­кость как бы «прилипает» к стенке. Этот факт — нулевая скорость у стен­ки — подтверждается бесчисленными измерениями, причем, как ни удивитель­но, падение скорости до нуля происходит независимо от материала стенки и от того, какая жидкость (или газ) течет.

Но раз это так, то в попереч­ном направлении существует градиент скорости, и в соответствии с уравне­нием (1) импульс будет переноситься от оси потока к стенке. Количественное рассмотрение этого переноса приводит к такому выводу.

В простейшем случае (поток в круг­лой трубе) скорость максимальна на оси трубы; здесь она в 2 раза больше, чем средняя скорость потока. Далее к стенкам скорость падает до нуля, и ха­рактер ее изменения описывается

парабо­лой. При этом во всех точках, равно­удаленных от оси, скорость одинакова. Частицы, находящиеся на равном рас­стоянии от оси, образуют цилиндриче­ский слой, движущийся с постоянной скоростью. Слои, более близкие к стен­кам, движутся медленнее, а более близ­кие к оси — быстрее. Такое тече­ние называют ламинарным (от латинского lатiпа — пластина, слой).

В конце концов, импульс, переноси­мый от оси к стенке, передается этой стенке. При этом происходит рассеяние энергии. Таким образом, описываемая передача импульса может рассматриваться как трение, на преодоление ко­торого нужно затрачивать энергию, т. е. речь идет о так называемом гидравли­ческом сопротивлении.

Теперь снова вернемся к шарикам, катящимся по желобкам. Пусть уклон дороги возрос, т. е. возросла и скорость. Тогда малейшая неровность одного из желобков приведет к тому, что шарик вылетит из него и перелетит в другой желобок. При этом он, вероятно, выбьет из этого желобка тот шарик, который там находился. Кроме того, и по этому желобку шарик прокатится недолго: лю­бая помеха, неровность — и шарик опять срывается со своей траектории и переле­тает в какой-то еще желобок. Через некоторое время картина будет такой: все шарики в беспорядке то движутся по каким-либо желобкам, то переле­тают из одного желобка в другой.

Так и с жидкостью. Если начать уве­личивать скорость, то в какой-то момент ламинарное течение станет неустойчи­вым. При любом возмущении («неров­ности желобка») частица сойдет со сво­его места в «строю» (в соответствую­щем цилиндрическом слое) и двинется куда-то в сторону, «расталкивая» те час­тицы, которые движутся там. Но ведь пространство трубы заполнено жид­костью, и если одна частица смести­лась, то не на свободное место, а на позицию, которая ранее была занята. Таким образом, в беспорядочное, хаоти­ческое движение окажутся вовлеченными многие частицы, а затем и весь поток.

Теперь картина потока иная. Жид­кость по-прежнему движется вдоль тру­бы. Но на это "движение накладывают­ся хаотические колебания (пульсации, флуктуации), происходящие в различных направлениях. Такой поток называют турбулентным (от латинского turbulentus — беспорядочный). Вы многократ­но сталкивались с этим явлением. По­лоскание флага на ветру или ветер, ко­торый то и дело меняется перед пере­меной погоды,— вот два проявления турбулентности атмосферы. В общих чер­тах турбулентный поток «устроен» сле­дующим образом. В текущей жидкости выделяются области, каждая из которых в данный момент движется приблизи­тельно как единое целое. Приблизитель­но, потому что все время происходит взаимное перемещение более мелких ча­стей этой области, причем в основном оно носит вихревой характер. Каждая такая область (частица) завихрена, по^: этому их часто так и называют — вихри.

Типичный пример турбулентного вих­ря — атмосферный циклон, представляю­щий собой весьма внушительный вихрь: масса воздуха, переносимая в нем, мо­жет составлять миллиарды тонн; но и это явно не предел. Солнечные пятна — тоже вихри в турбулентной атмосфере Солнца, вихри, по сравнению с которыми Земля — как горошина рядом с речным водоворотом. И пожалуй, каждая галак­тика тоже может рассматриваться как вихрь в турбулентной Вселенной.

Вихрь в потоке (не будем говорить о галактиках) существует недолго. Тур­булентные пульсации «растаскивают», разрывают его на более мелкие вихри, те, в свою очередь, распадаются на еще более мелкие. Но параллельно образуют­ся новые большие вихри, и вся эта слож­ная картина многократно повторяется.

Может возникнуть вопрос: а разве в ламинарном потоке нет возмущений? Неужели там уж все так гладко? Воз­мущения, конечно, есть. Но вспомним нашу модель — дорогу с желобками. Пока скорость была невелика, возмуще­ния гасили стенки желобка. В ламинар­ном потоке эту роль играет вязкость. «Возмутившаяся» частица отдает изли­шек импульса окружающим, те — даль­ше, и опять они движутся, «как все». Когда же скорость (и импульс) растет, сил вязкости уже не хватает, чтобы удер­жать частицу «в желобке». Возникает турбулентность. Поэтому условия пере­хода от ламинарного режима к турбу­лентному определяются соотношением между скоростью и вязкостью. Мерой этого соотношения является число Рейнольдса, или критерий Рейнольдса,— ве­личина, названная в честь О. Рейнольд­са, замечательного английского ученого, около 200 лет назад впервые изучившего переход из ламинарного режима течения в турбулентный. Число Рейнольдса Rе имеет вид:

,

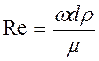где ω— скорость, d— размер, ха­рактеризующий данный поток, ρ и μ— соответственно плотность и вязкость жидкости. Если поток движется в трубе круглого сечения и d— ее диаметр, то при Rе<2320 устойчивым будет ла­минарный режим, при Rе>10 000 — турбулентный, а в промежутке будет наб­людаться переменный режим. Правда, если трубу тщательно отполировать, что­бы исключить возмущения, то удается продлить область ламинарности до зна­чительно больших значений Rе, но ма­лейшая встряска — и наступает турбу­лентный режим.

Важнейшая для химической техноло­гии особенность турбулентного потока — это характер процессов переноса в нем. Представим себе ламинарный поток на грани перехода в турбулентный. Пусть в результате возмущения одна из ча­стиц, движущаяся вдоль оси трубы (и по­этому имеющая максимальную ско­рость), начинает смещаться к стенке. При этом она переносит в периферий­ную зону потока свою большую продоль­ную составляющую импульса. Вдобавок, как сказано выше, она вытеснит более медленную частицу, которая будет сме­щаться ей навстречу, перенося свой ма­лый импульс и уменьшая скорость осевой части потока. Скорости будут выравни­ваться по сечению.

Ясно, что описанная картина вырав­нивания скоростей аналогична картине переноса импульса механизмом вязкости. Разница лишь в том, что здесь пере­нос — конвективный (переносят импульс не молекулы, а частицы, состоящие из огромного числа молекул), и поэтому его мощность неизмеримо выше. Если выразить закономерности переноса урав­нением (1), то коэффициент окажется очень большим. Теперь это уже не мо­лекулярная вязкость μ, а турбулентная вязкость μ_т, обусловленная турбулентны­ми пульсациями. В соответствии с большой величиной (μ_т производная в правой части уравнения (1) должна быть мала (иначе произведение дало бы нереальное значение потока ρ_тω)- Это значит, что наклон кривой, изображающей распреде­ление скорости по поперечному сечению, мал. Это уже не парабола, а очень пло­ская кривая, так как перемешивание ча­стиц выравнивает скорости.

Наряду с турбулентной вязкостью можно говорить о турбулентной тепло­проводности и турбулентной диффузии. Турбулентность интенсивно перемеши­вает жидкость в поперечном направле­нии, перенося тепло и вещество, вырав­нивая температуру и концентрации всех веществ. Именно поэтому для химиче­ской технологии типичны турбулентные потоки, а турбулизация — один из важ­ных приемов интенсификации процессов.

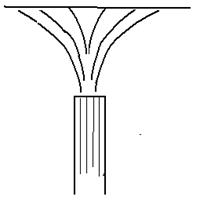
Рис.2 Схема потока направленного на стенку

Но картина турбулентного потока по­ка не полна. Необходимо рассмотреть еще одну важную его особенность: по­ведение потока у стенок. Здесь опреде­ляющую роль играют два обстоятель­ства. Во-первых, у самой стенки скорость и в турбулентном потоке тоже падает до нуля; во-вторых, если направить по­ток прямо на поверхность твердого тела (например, пустить из сопла струю воз­духа, как показано на рис. 2), то он не дойдет до поверхности, а «расплю­щится» и начнет обтекать тело. То же самое происходит с турбулентными пуль­сациями. Они не способны дойти до са­мой стенки и вблизи от стенки повора­чивают и начинают двигаться вдоль нее. В результате турбулентный перенос за­тухает. В непосредственной близости от стенки образуется тонкий (так называе­мый пограничный) слой, где перенос осу­ществляется в основном за счет молеку­лярного механизма*.(* Описанная здесь картина упрощена. Сам по­граничный слой обладает сложной структурой, и молекулярные механизмы лимитируют процесс только в части его — подслое. Но для нашего изложения это несущественно) Основную часть по­тока, за вычетом пограничного слоя, обычно называют ядром.

Перенос импульса в пограничном слое осуществляется молекулярной вяз­костью. Так как μ<<μ_T, градиент скоро­сти здесь велик: скорость резко падает от большого значения, существующего в ядре, до нуля у стенки.

То же самое происходит с перено­сом тепла и вещества. В ядре потока температура и концентрации выровнены турбулентным перемешиванием, а в по­граничном слое происходит резкое изме­нение этих величин. Дальше мы в основ­ном будем говорить о переносе вещест­ва, который наиболее специфичен для химико-технологических процессов. Рассмотрим поток, в котором движет­ся раствор какого-либо вещества, при­чем на стенках это вещество расходуется (например, кристаллизуется или всту­пает в реакции). Тогда профиль кон­центраций будет таким, как изображено на рис. 3.

Точное описание изображенной на рисунке картины потребовало бы слож­ного количественного анализа механиз­мов переноса в турбулентном потоке и в пограничном слое. К сожалению, стро­гая теория турбулентного потока до сих пор не создана, поэтому при анализе процессов пользуются теми или иными упрощенными моделями.

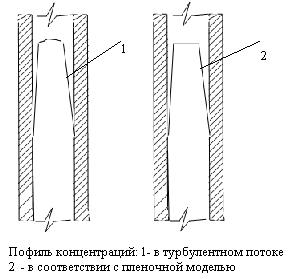
Разберем простейшую модель. Ее предложил выдающийся немецкий физико-химик В. Нернст. Нернст, рассматривая процессы растворения твердых веществ и изучая скорость растворения, пришел к выводу, что процесс можно описать следующей схемой. В ядре потока кон­центрация растворяемого вещества рас­пределена равномерно благодаря интенсивному перемешиванию. Но у поверхно­сти твердого тела существует как бы неподвижная пленка, через которую рас­творяемое вещество диффундирует в ядро. Пользуясь современными представ­лениями, естественно сопоставить эту пленку с пограничным слоем. Разумеется, жидкость в нем движется, но для схемы Нернста это не важно. Важно, что пере­нос здесь происходит на молекулярном уровне. Правда, в действительности все гораздо сложнее. Если воспользоваться схемой Нернста (пленочной моделью), то распределение, показанное на рис. 3, преобразуется в картину, изображенную на рис. 4; в ней «срезаны» все закруг­ления, в ядре — полная равномерность, пленка четко отграничена от ядра. В реальном же потоке ядро постепенно переходит в пограничный слой, причем как толщина слоя, так и характер пе­рехода зависят от степени развития тур­булентности. Но для качественного опи­сания пленочная модель оказалась на­столько удобной, что ею широко поль­зуются до сих пор.

Рассмотрим в рамках пленочной мо­дели уравнение (3). Если в пленке не идет реакция, то вещество там не рас­ходуется и не образуется, поэтому по­ток ц не меняется с расстоянием: сколь­ко вещества вошло в пленку с одной стороны, столько же выйдет с другой. Но тогда правая часть уравнения по­стоянна, и в этом случае производная 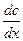просто равна разности концентраций с разных сторон пленки, деленной на толщину пленки δ: q_m=D(c₂-c₁)/δ. Это уравнение легко привести к виду:

q_m=β∆c, (4)

где ∆с — разность концентраций между ядром потока и стенкой (ее обычно на­зывают движущей силой массоотдачи); β — коэффициент массоотдачи. Уравне­ние (4) — основная формула, по ко­торой рассчитывают процессы переноса вещества; в нем

β = D /δ (5)

Так же получается уравнение пере­носа тепла (а — коэффициент тепло­отдачи) :

д_я=аАТ. (6)

Влияние потока отражается на вели­чинах β и а, которые определяются тол­щиной пограничного слоя δ. Чем быст­рее поток, чем больше число Рейнольдса, тем сильнее развита турбулентность турбулентные пульсации подходят ближе к поверхности, т. е. δ уменьшается, β и а растут.

Обратите внимание на следующее В ядре потока действуют и конвекция и молекулярные механизмы. Но когда мы обсуждали выравнивание концентраций (скоростей, температур) в ядре, мы го­ворили только о турбулентном перемеши­вании, о конвекции. Это потому, что оба механизма здесь действуют параллельно и лимитирует более мощная конвекция

Если же рассмотреть поперечный пе­ренос в целом, то процесс распадается на две последовательные стадии: вна­чале перенос в ядре, затем — через пограничный слой (если перенос идет от стенки, то пограничный слой — внача­ле, но это не принципиально). Раз ста­дии последовательны, то лимитирует мед­ленная, т. е. перенос в пограничном слое. И воздействовать надо именно на этот слой — только так можно существенно ускорить процесс.

Как же это делается? Главный спо­соб интенсификации — увеличение ско­рости потока. Почему мы мерзнем на ветру? Потому, что через тонкий погра­ничный слой интенсивно теряется тепло На том же ветру быстро сохнет белье, ибо одновременно растут скорости от­дачи и тепла, и влаги.

В химической технологии есть две большие группы процессов, по существу сводящихся к переносу. Это теплообменные процессы (нагревание или охлаждение) и массообменные процессы. Набор массообменных процессов чрезвычайно широк. Это поглощение веществ из газа жидкостью (абсорбция); поглощение из газов или жидкостей поверхностью твер­дых тел (адсорбция); перегонка жидко­стей; выделение веществ из растворов путем растворения в другой жидкости (экстракция). Сюда же относятся рас­творение, кристаллизация, сушка.

В этих процессах почти всегда уве­личение скорости потока приводит к ин­тенсификации переноса вещества. В большинстве современных типов мас­сообменных и теплообменных аппаратов создаются высокие скорости потоков. Но такая интенсификация даром не дается. Чем больше скорость, тем выше гидрав­лическое сопротивление, тем больше по­тери энергии. Значительные усилия кон­структоров направляются на создание таких аппаратов, где сопротивление сни­жено.

В некоторых случаях интенсифициро­вать поперечный перенос тепла и вещест­ва удается не за счет повышения ско­рости, а путем создания особой конфигу­рации поверхности, вдоль которой дви­жется поток.