Структура математической модели химического реактора
Методы расчета и проектирование химических реакторов основаны на моделировании реакторов и процессов в них.
Моделирование - это метод изучения разных объектов, при котором исследование проводят на модели, а результаты количественно распространяют на оригинал. Модель может представлять собой уменьшенную по определенным законам (или в некоторых случаях увеличенную) копию реального объекта. Но моделью может быть и определенная система представлений о реальном объекте, который выражается как совокупность математических структур, уравнений, неравенств, таблиц, графиков. Такую модель называют математическим описанием объекта или его математической моделью.
Математическая модель химического реактора должна быть с одного стороны довольно простой, с другой стороны - довольно точно передавать количественные закономерности протекания процесса. Эти требования находятся в противоречии и разработка математической модели очень сложная задача.
Модель- специально созданный объект любой природы, более простой по сравнению с исследуемым по всем свойствам, кроме тех, которые надо изучить, и способный заменить исследуемый объект так, чтобы можно было получить новую информацию о нем.
Известный пример моделирования: обтекание самолета, летящего в воздухе, исследуют обтеканием его модели в аэродинамической трубе, В данном случае модель самолета - его геометрически подобная уменьшенная копия. Моделируется (исследуется) только обтекание корпуса самолета потоком воздуха и не исследуются другие свойства самолета, например удобство и безопасность пассажира в кресле. Для этого надо построить другую модель - отдельное кресло с манекеном на устройстве, воспроизводящем возможные его положения в полете. Как видим, модель учитывает какие-то явления (обтекание корпуса самолета потоком воздуха в одном случае или расположение человека в кресле в другом случае при моделировании разных процессов в самолете) и параметры процессов (конфигурация крыльев и корпуса или конфигурация кресла). Учитываемые в модели явления назовем составляющими модели.
Модель специально создают, чтобы исследовать какие-либо конкретные свойства. Для изучения разных свойств объекта может быть создано несколько его моделей, каждая из которых отвечает определенной цели исследования. Можно говорить о единстве "цель - модель". Если модель отражает большее (или меньшее) число свойств, то она называется более широкой (или более узкой). Используемое иногда понятие "общая модель" как модель, отражающая все свойства объекта, - бессмысленно по сути.
Чтобы достигнуть поставленной цели, на изучаемые свойства модели должны оказывать влияние те же факторы, что и на свойства объекта. В этом и заключается творческий и научный подход к построению модели: учесть именно те явления, которые существенны для изучаемых свойств. Не все составляющие и параметры в одинаковой степени влияют на изучаемые свойства. Изменение некоторых параметров и наличие тех или иных составляющих может очень слабо влиять на эти свойства. Такие составляющие и параметры называют несущественными, и их можно не учитывать в модели. Соответственно, простая модель содержит лишь существенные составляющие, иначе модель будет избыточной. Поэтому простая модель не есть простая по внешнему виду (например, несложная по структуре, конструкции). Но если в модель входят не все составляющие, существенно влияющие на изучаемые свойства, то она будет неполной, и результаты ее исследования могут не отвечать свойствам объекта.
Обратим внимание на следующий признак модели: она должна предсказывать неизвестные свойства объекта, давать о нем новую информацию. Это может быть достигнуто, во-первых, если модель простая, и ее можно исследовать, работать с ней, и, во-вторых, если она достаточно полная, чтобы могли проявиться изучаемые свойства.
Впервые моделирование как метод научного познания был использован в аэро- и гидродинамике. Была развита теория подобия, позволяющая переносить результаты экспериментов, получаемых на установках небольшого масштаба (моделях), на реальные объекты большого масштаба. Основой таких исследований является физическое моделирование,при котором природа модели и исследуемого объекта одна и та же. Физическое моделирование и теория подобия нашли широкое применение в химической технологии при исследовании тепловых и диффузионных процессов. Были сделаны попытки использовать теорию подобия и для химических процессов и реакторов. Однако ее применение здесь оказалось весьма ограниченным из-за несовместимости условий подобия для химических и физических составляющих процесса в реакторах разного масштаба. Например, степень превращения реагентов зависит от времени пребывания их в реакторе, равного отношению размера к скорости потока. Условия тепло- и массопереноса, как следует из теории подобия, зависит от критерия Рейнольдса, пропорционального произведению размера на скорость. Сделать одинаковыми в аппаратах разного масштаба и отношение, и произведение двух величин невозможно. Вклад химических и физических составляющих реакционного процесса и их взаимовлияние и, следовательно, влияние их на результаты процесса в целом зависят от масштаба. В аппарате небольшого размера выделяющаяся теплота легко теряется и слабо влияет на скорость превращения. В аппарате большого размера выделяющаяся теплота легче "запирается" в реакторе, существенно влияет на поле температур и, следовательно, на скорость и результаты протекания реакции. Вклад физических составляющих в реакционный процесс в аппарате большого масштаба становится существенным.
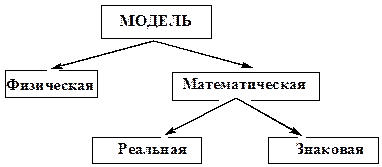
Рис. 4. Классификация моделей
Трудности масштабного перехода для реакционных процессов удается преодолеть, используя математическое моделирование,в котором модель и объект имеют разную физическую природу, но одинаковые свойства. Два устройства - механический маятник и замкнутый электрический контур, состоящий из конденсатора и катушки индуктивности, - имеют разную физическую природу, но одинаковое свойство: колебания механические и электрические соответственно. Можно так подобрать параметры этих устройств (длину маятника и отношение емкости к индуктивности), что колебания по частоте будут одинаковыми. Тогда электрический колебательный контур будет моделью маятника. Это возможно потому, что свойство обоих устройств - колебания - описывается одними и теми же уравнениями. Отсюда и название вида моделирования - математическое. Уравнение колебания в данном случае также является математической моделью и механического маятника, и электрического контура. Соответственно, математические модели подразделяются на реальные, представленные неким физическим устройством, и знаковые, представленные математическими уравнениями. Классификация моделей приведена на рис. 4.
Естественно, для построения реальной математической модели надо сначала создать знаковую. Поэтому, как правило, математическую модель отождествляют только с уравнениями, описывающими объект, т. е. со знаковой математической моделью, а исследование свойств этих уравнений называют математическим моделированием. Универсальной реальной математической моделью является электронная вычислительная машина (ЭВМ). По уравнениям, описывающим объект, ЭВМ "настраивают" (программируют), и ее "поведение" будет описываться этими уравнениями.
Поскольку влияние физических и химических составляющих (явлений) на реакционный процесс зависит от масштаба, именно их выделение - наиболее существенный момент в математическом моделировании химических процессов и реакторов. В общем виде математическое моделирование реакторов можно представить схемой, показанной на рис. 5.
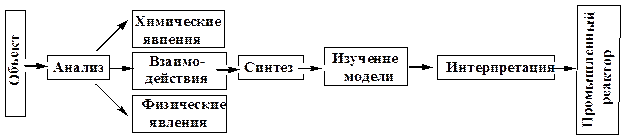 Рис. 5. Схема математического моделирования химических процессов и реакторов
Рис. 5. Схема математического моделирования химических процессов и реакторов
Ответственным этапом является анализ процесса, протекающего в химическом реакторе; анализ выявляет составляющие процесса и их взаимодействие. Затем определяют их закономерности: термодинамические и кинетические для химических превращений, параметры явлений переноса и т. д. На этом этапе используют данные экспериментальных исследований. Математическое моделирование не исключает эксперимент, а активно его использует, но эксперимент прецизионный, более точный, чем может быть эксперимент на реакторе. Результаты анализа процесса и исследования его составляющих позволяют построить математическую модель процесса - уравнения, описывающие его. Их исследуют, используя математический аппарат качественного анализа и вычислительные методы, или, как говорят, проводят вычислительный эксперимент. Полученные свойства модели надо интерпретировать как свойства изучаемого объекта, в данном случае химического реактора.
Выделение составляющих сложного процесса (его декомпозиция) должно отвечать также условию инвариантности выделенных составляющих к масштабу, влияние которого учитывают в параметрах полученных уравнений математической модели и граничных условиях. Требование инвариантности можно удовлетворить, если использовать иерархический подход к построению модели. Для этого декомпозицию процесса проводят не только на составляющие, но и по их масштабу. Существенной особенностью математических моделей процесса в реакторах является их иерархическое строение (рис..6).
В молекулярном масштабе протекает химическая реакция, состоящая из элементарных стадий. Ее свойства (например, скорость) не зависят от масштаба реактора, т. е. скорость реакции зависит от условий ее протекания независимо от того, как эти условия созданы. Результатом исследования на этом уровне является кинетическая модель – зависимость скорости реакции от условий. Следующий масштабный уровень, назовем его химический процесс, есть совокупность реакции и явлений переноса, таких, как диффузия, теплопроводность. Кинетическая модель реакции входит как одна из составляющих. Объем, в котором рассматривается химический процесс, выбирается так, чтобы закономерности процесса не зависели от размера реактора. Например, это может быть зерно катализатора. Скорость превращения в нем зависит только от размера и характеристик зерна и от условий (концентрация и температура), в которых оно находится, независимо от того, как эти условия созданы. Модель химического процесса входит как одна из составляющих на следующем масштабном уровне - реакционная зона. Другие составляющие - явления переноса -такого же масштаба. В масштабе реактора входят как составляющие реакционная зона, узлы смешения, теплообмена и др. Таким образом, математическая модель процесса в реакторе представлена системой математических моделей разного масштаба.
 Рис. 6. Иерархическая структура математической модели процесса в химическом реакторе
Рис. 6. Иерархическая структура математической модели процесса в химическом реакторе
Иерархическая структура математической модели процесса в реакторе позволяет:
полностью описать свойства процесса путем детального исследования основных процессов разного масштаба;
проводить изучение сложного процесса по частям, применяя к каждой из них специфические, прецизионные методы исследования, что повышает точность и надежность результатов;
установить связи между отдельными частями и выяснить их роль в работе реактора в целом;
облегчить изучение процесса на более высоких уровнях, так как исследованием процесса на низшем уровне укрупняется информация при переходе на более высокий уровень;
решать задачи масштабного перехода.
Изучение процесса в химическом реакторе будем проводить описанным выше научным методом - математическим моделированием.
При разработке математической модели целесообразно использовать иерархический подход к реактору как к сложной системе. (Иерархия - это расположение частей элементов целого в порядке от высшего до низшего). Суть этого подхода заключается в том, что сложная система рассматривается как совокупность подсистем, связанных между собой.
Реактор и реакционный узел, будучи сложными объектами, имеют многоступенчатую структуру и их математические модели строятся последовательно на основе предыдущего построения их составных частей и введение соотношений, которые связывают переход с одного уровня на другой.
Важную роль математического описания химического реактора играют балансовые уравнения, являющиеся выражением общих законов сохранения массы и энергии.
Материальный баланс — один из важнейших методов описания и анализа химико-технологических процессов. Он выражает закон сохранения вещества; уравнение баланса соответствует утверждению: приход вещества равен расходу вещества. При описании химических реакций в потоке обычно записывают отдельное уравнение баланса для каждого из веществ.
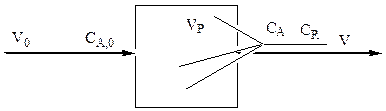
Рис. 7. Схема материальных потоков в аппарате смешения
nj вх – nj вых -nj Xр = nj нак ,
где nj вх – количество вещества j, внесенное в элементарный объем ΔV за время Δτ с потоком участников реакции.
Qвх – Qвых Qхр 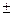 Qт.о. = Qнач
Qт.о. = Qнач
Qвх – теплосодержание веществ, входящих в объем ΔV за время Δτ;
Qхр – теплота, выделившаяся или поглотившаяся в результате химической реакции;
Qт.о – теплота, израсходованная на теплообмен объема ΔV за время Δτ;
Для составления материального баланса по веществу А будем считать, что объемный расход реакционной смеси на входе в реактор V0, м3/ч, на выходе V. Концентрация вещества А в потоке, входящем в реактор CA,0, кмоль/м3, концентрация вещества А в выходящем потоке и в любой точке реактора составляет CA, кмоль/м3, химическая реакция протекает со скоростью ωA кмоль/м3 ч, определяемый и рассматриваемый промежуток времени dτ, при постоянной температуре, концентрации CA.
Тогда за время dτ в объем реактора V войдет nA вх = CA,0 V0 dτ, выйдет из реактора nA вых = CA V dτ. Израсходуется на химическую реакцию nA х.р. = ω Vр dτ.
Так как в реакторе находится CAVр моль вещества А, изменение этого количества за время dτ составит nA нак = d (CA Vр)
Таким образом уравнение материального баланса по веществу А для реактора идеального смешения имеет вид
CA,0 V0 dτ - CA V dτ – ωA Vр d τ = d (CA Vр)
Все члены этого уравнения измеряются в единицах количества вещества (кмоль). Разделим левую и правую часть на d τ
CA,0 V0 - CA V - ω Vр = 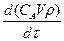 (1) - мольные потоки вещества в единицу времени. Правая часть уравнения представляет собой скорость накопления вещества в реакторе. При постоянном объеме Vр скорость накопления можно представить
(1) - мольные потоки вещества в единицу времени. Правая часть уравнения представляет собой скорость накопления вещества в реакторе. При постоянном объеме Vр скорость накопления можно представить
Vр dCA / dτ
Рассмотрим отдельный случай. Периодический реактор идеального смешения по условию
V0 = 0, V = 0.
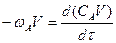 или
или 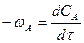
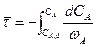 CA = CA,0 (1 – XA)
CA = CA,0 (1 – XA)
dCA = - CA,0 dXA
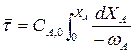
Дата добавления: 2017-01-08; просмотров: 3305;











