Математические аналоговые модели процесса
Практически все встречающиеся в технологических объектах процессы можно описать однотипными математическими уравнениями динамики, обобщенный аналог которых может быть представлен в виде
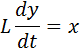
| (1) |
где
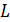 - емкостный коэффициент объекта;
- емкостный коэффициент объекта;
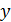 – выходная координата объекта (параметр);
– выходная координата объекта (параметр);
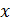 – обобщенная входная координата (результирующее входное воздействие
– обобщенная входная координата (результирующее входное воздействие
В качестве примера можно представить, как наиболее наглядную модель, модель простого одноемкостного гидравлического объекта. На этой модели ab = s – емкостный коэффициент, представляющий собой площадь основания сосуда.
| Функциональная зависимость физических процессов | Определение функций идеализированных физических процессов |
обобщенный аналог
функциональности
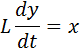
| 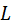 - емкостный коэффициент объекта; - емкостный коэффициент объекта;
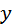 – выходная координата объекта
(параметр); – выходная координата объекта
(параметр);
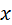 – обобщенная входная координата
(результирующее входное воздействие). – обобщенная входная координата
(результирующее входное воздействие).
|
для поступательного движения
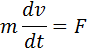
| 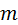 – масса движущегося тела; – масса движущегося тела;
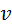 – линейная скорость; – линейная скорость;
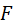 – результирующая действующая сила. – результирующая действующая сила.
|
для вращательного движения
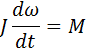
| 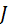 – момент инерции вращающегося тела
ω – угловая частота вращения
M – результирующий момент силы – момент инерции вращающегося тела
ω – угловая частота вращения
M – результирующий момент силы
|
для жидкостей в сосуде
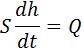
| S – площадь основания сосуда;
h – уровень жидкости в сосуде;
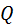 – объемный поток жидкости. – объемный поток жидкости.
|
для газовых сосудов
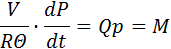
| V – объем сосуда;
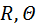 – газовая постоянная и абсолютная температура;
P,p – давление и плотность газа; – газовая постоянная и абсолютная температура;
P,p – давление и плотность газа;
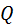 , М – объемный и массовый поток газа. , М – объемный и массовый поток газа.
|
для нагревания (охлаждения) тел
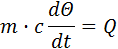
| 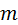 – масса нагреваемого тела; – масса нагреваемого тела;
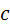 – теплоемкость удельная; – теплоемкость удельная;
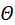 – температура тела; – температура тела;
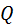 – тепловой поток. – тепловой поток.
|
для увлажнения (сушки) тел
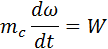
| 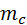 – масса сухого вещества; – масса сухого вещества;
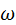 – влажность; – влажность;
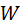 – поток влаги. – поток влаги.
|
Такой моделью-аналогом может быть представлен любой простейший одноемкостный объект, связь между координатами которого выражается обобщенной формулой (1).
Величины, характеризующие физические процессы.
Выходная координата y представляет собой абстрактный аналог ряда физических величин: линейной скорости v , окружной скорости ɷ, температуры Ɵ, влажности φ, концентрации вещества «с» и т.п. Практически это есть либо потенциал энергии, либо показатель запаса вещества в объекте.
В технологических объектах этими величинами характеризуется показатель качества процесса, его параметр.
Из приведенных выше уравнений физических моделей процессов четко прослеживается сущность емкостного коэффициента 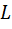 . Это есть величина, численно равная емкости объекта, приходящейся на единицу его выходной координаты.
. Это есть величина, численно равная емкости объекта, приходящейся на единицу его выходной координаты.
Если представить уравнение (1) в виде
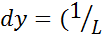 ) xdt ) xdt
| (2) |
и проинтегрировать его
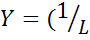 )xdt )xdt
| (3) |
То можно увидеть, что величина, обратная емкостному коэффициенту 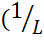 ), есть коэффициент пропорциональности между элементарными изменениями выходной координаты y и импульсом входного воздействия xdt.
), есть коэффициент пропорциональности между элементарными изменениями выходной координаты y и импульсом входного воздействия xdt.
Таким воздействием может быть:
- импульс силы Pdt,
- импульс момента Mdt,
- импульс подачи какого-либо вещества,
- импульс тепловой энергии Ɵdt и т.п.
В итоге можно заключить, что емкостный коэффициент есть мера инертности, а его обратная величина 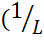 ) – мера чувствительности объекта.
) – мера чувствительности объекта.
ПРИЛОЖЕНИЕ.
ПРОСТЕЙШИЕ ОДНОЕМКОСТНЫЕ ПРОЦЕССЫ
Передаточная функция статического объекта управления - это изменение во времени выходной координаты одноемкостного процесса, как было показано выше, характеризуется обобщенным уравнением
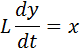
|
Очевидно, условием постоянства выходной координаты объекта (y=const) является равенство результирующего входного воздействия х нулю:
| dy/dt = (1/L)x=0 |
Это условие характеризует установившийся (на определенном уровне) режим объекта – индекс «нуль».
В общем случае результирующий мгновенный поток вещества или энергии – входное воздействие объектов – состоит из разницы между суммарным притоком
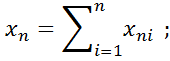
|
и суммарным расходом
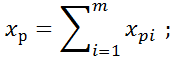
|
то есть
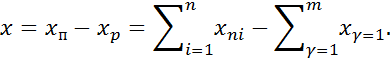
|
Следовательно при установившемся режиме объекта, т.е. при y = y0= const
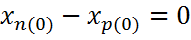 или или 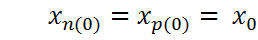
|
Предположим, что к моменту начала исследования приток численно равен расходу и объект находится в установившемся режиме при значении выходной координаты y0 .
В этот момент как на стороне притока, так и на стороне расхода может быть приложено дополнительное воздействие (регулирующее или возмущающее) Δx , которое должно вывести объект из установившегося состояния.
Если воздействие приложено на стороне притока, то параметр должен возрастать, и наоборот.
При этом необходимо иметь в виду, что как возмущение, так и регулирующее воздействие может выполнять функции притока или расхода.
Допустим, что дополнительное воздействие на объект внесено на стороне притока. Тогда приток соответственно увеличится на какую-то величину Δxп , т.е.
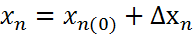
|
а расход остается прежним
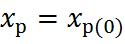
|
С течением времени под воздействием дополнительного притока выходная координата будет возрастать. Это, в свою очередь, может вызвать изменение значений входных воздействий (возмущение и регулирующих). Если они находятся в функциональной зависимости от выходной координаты:
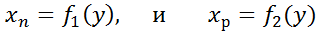
|
Например, нетрудно представить, что с изменением температуры воздуха в помещении (выходной координаты) соответственно будут изменяться приток теплоты от отопительных батарей и расход ее через окна и ограждения (входные величины).
Эти зависимости могут быть линейными или различной степени нелинейности. В общем случае, воспользовавшись формулой Тейлора для разложения в ряд функции одного независимого переменного и учитывая лишь два его первых члена, можно записать
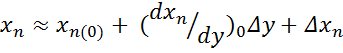
|
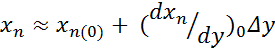
|
где  – отклонение выходной координаты от исходного установившегося (нулевого) значения.
– отклонение выходной координаты от исходного установившегося (нулевого) значения.
Величина 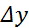 – переменная во времени. Индекс «нуль» при производных указывает на то, что их определяют для исходного режима, и, следовательно, они постоянные величины. Очевидно. Наиболее точным выражением производных будет их значение в пределах оптимального значения параметра, то есть индекс «нуль» необходимо выбирать при y
– переменная во времени. Индекс «нуль» при производных указывает на то, что их определяют для исходного режима, и, следовательно, они постоянные величины. Очевидно. Наиболее точным выражением производных будет их значение в пределах оптимального значения параметра, то есть индекс «нуль» необходимо выбирать при y 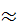 yn .
yn .
Подставив значения текущих координат хп и хр из формул в обобщенное уравнение динамики:
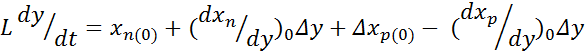
проводим преобразования, получим
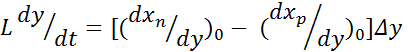 +
+ 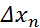
или
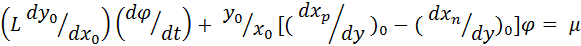
Коэффициент у первого члена уравнения есть время Та , необходимое для заполнения емкости при полной нагрузке. Его называют временем астатического разгона объекта:
Та = L 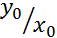
|
Величина обратная времени Та характеризует скорость относительного изменения выходной координаты y процесса при 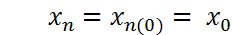
ξ=1/Та = 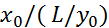
называется скоростью разгона при полной нагрузке.
Если нагрузка меньше полной, то соответственно скорость разгона будет меньше, а время разгона будет соответственно больше.
Коэффициент при втором члене φ левой части уравнения безразмерный , так как сомножители имеют противоположные размерности. Его называют коэффициентом статизма, или самовыравнивания объекта (процесса):
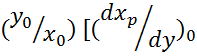 -
- 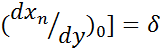
Как видно, этот коэффициент характеризует зависимость входных воздействий объекта от выходной координаты.
Окончательно уравнение динамики, описывающее поведение простого одноемкостного объекта во времени при наличии некомпенсированного входного воздействия, приобретает вид:
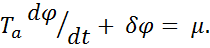
Форма уравнения, в которой коэффициент при входной координате есть единица, впервые была предложена известным словацким инженером А. Стодолой и получила название уравнения А. Стодолы.
Часто пользуются другой (так называемой канонической) формой уравнения динамики процесса, когда коэффициент при φ равен единице:
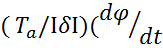 )
) 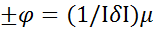 ,
,
Поскольку 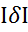 - величина безразмерная, то при делении времени разгона
- величина безразмерная, то при делении времени разгона 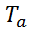 на δ получаем постоянную времени объекта (процесса):
на δ получаем постоянную времени объекта (процесса):
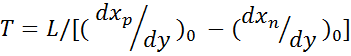 .
.
Дата добавления: 2021-04-21; просмотров: 569;











