Нейронные сети. Продвинутые конфигурации
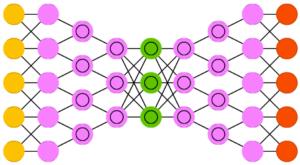
Глубинные свёрточные обратные графические сети(deep convolutional inverse graphics networks, DCIGN) названы слегка некорректно, поскольку они по сути являются вариационными автокодировщиками, кодирующая и декодирующая части которых представлены свёрточной и развёртывающей НС соответственно. Сети такого типа моделируют свойства в виде вероятностей, поэтому их можно научить создавать картинку с собакой и кошкой, даже если сеть видела только картинки, на которых было только одно из животных. Возможно и удаление одного из двух объектов. Также были созданы сети, которые могли менять источник освещения и вращать объект. Сети такого типа обычно обучают методом обратного распространения ошибки.
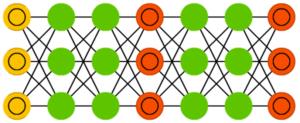
Генеративные состязательные сети(generative adversarial networks, GAN) — это сети другого вида, они похожи на близнецов. Такие сети состоят из любых двух (обычно из FF и CNN), одна из которых контент генерирует, а другая — оценивает. Сеть-дискриминатор получает обучающие или созданные генератором данные. Степень угадывания дискриминатором источника данных в дальнейшем участвует в формировании ошибки. Таким образом, возникает состязание между генератором и дискриминатором, где первый учится обманывать первого, а второй — раскрывать обман (похоже на ситуацию «банкир-фальшивомонетчик»). Обучать такие сети весьма тяжело, поскольку нужно не только обучить каждую из них, но и настроить баланс.
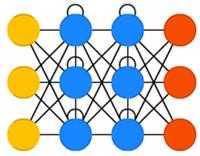
Рекуррентные нейронные сети(recurrent neural networks, RNN) — это сети типа FFNN, но с особенностью: нейроны получают информацию не только от предыдущего слоя, но и от самих себя предыдущего прохода. Это означает, что порядок, в котором вы подаёте данные и обучаете сеть, становится важным. Большой сложностью сетей RNN является проблема исчезающего (или взрывного) градиента, которая заключается в быстрой потере информации с течением времени. Конечно, это влияет лишь на веса, а не состояния нейронов, но ведь именно в них накапливается информация. Обычно сети такого типа используются для автоматического дополнения информации.
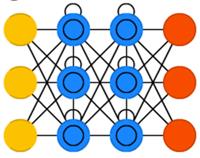
Сети с долгой краткосрочной памятью(long short term memory, LSTM) стараются решить вышеупомянутую проблему потери информации, используя фильтры и явно заданную клетку памяти. У каждого нейрона есть клетка памяти и три фильтра: входной, выходной и забывающий. Целью этих фильтров является защита информации. Входной фильтр определяет, сколько информации из предыдущего слоя будет храниться в клетке. Выходной фильтр определяет, сколько информации получат следующие слои. Ну а забывающий фильтр, каким бы странным не казался, также выполняет полезную функцию: например, если сеть изучает книгу и переходит на новую главу, какие-то символы из старой можно забыть. Такие сети способны научиться создавать сложные структуры, например, писать как Шекспир или сочинять простую музыку, но и ресурсов они потребляют немало.
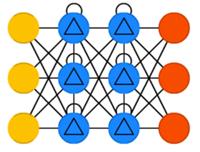
Управляемые рекуррентные нейроны(gated recurrent units, GRU) — это небольшая вариация предыдущей сети. У них на один фильтр меньше, и связи реализованы иначе. Фильтр обновления определяет, сколько информации останется от прошлого состояния и сколько будет взято из предыдущего слоя. Фильтр сброса работает примерно как забывающий фильтр.
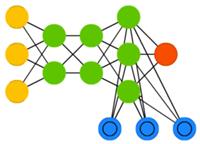
Нейронные машины Тьюринга(neural Turing machines, NTM) можно рассматривать как абстрактную модель LSTM и попытку показать, что на самом деле происходит внутри нейронной сети. Ячейка памяти не помещена в нейрон, а размещена отдельно с целью объединить эффективность обычного хранилища данных и мощь нейронной сети. Собственно, поэтому такие сети и называются машинами Тьюринга — в силу способности читать и записывать данные и менять состояние в зависимости от прочитанного они являются тьюринг-полными.
Двунаправленные RNN, LSTM и GRU (bidirectional recurrent neural networks, bidirectional long / short term memory networks и bidirectional gated recurrent units, BiRNN, BiLSTM и BiGRU) не показаны в таблице, поскольку они ничем не отличаются от своих однонаправленных вариантов. Разница заключается в том, что эти сети используют не только данные из «прошлого», но и из «будущего». Например, обычную сеть типа LSTM обучают угадывать слово «рыба», подавая буквы по одной, а двунаправленную — подавая ещё и следующую букву из последовательности. Такие сети способны, например, не только расширять изображение по краям, но и заполнять дыры внутри.
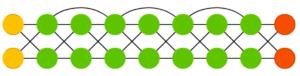
Глубинные остаточные сети(deep residual networks, DRN) — это очень глубокие сети типа FFNN с дополнительными связями между отделёнными друг от друга слоями. Такие сети можно обучать на шаблонах глубиной аж до 150 слоёв — гораздо больше, чем можно было бы ожидать. Однако, было показано, что эти сети мало чем отличаются от рекуррентных, и их часто сравнивают с сетями LSTM.
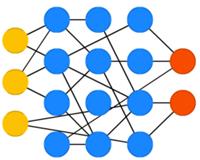
Нейронная эхо-сеть(echo state networks, ESN) — это ещё одна разновидность рекуррентных сетей. Её особенностью является отсутствие сформированных слоёв, т.е. связи между нейронами случайны. Соответственно, метод обратного распространения ошибки не срабатывает. Вместо этого нужно подавать входных данные, передавать их по сети и обновлять нейроны, наблюдая за выходными данными.

Метод экстремального обучения(extreme learning machines, ELM) — это, по сути, сеть типа FFNN, но со случайными связями. Они очень похожи на сети LSM и ESN, но используются как FFNN. Так происходит не только потому, что они не рекуррентны, но и потому, что их можно обучать просто методом обратного распространения ошибки.
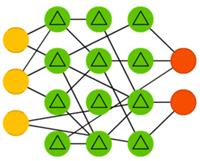
Метод неустойчивых состояний(liquid state machines, LSM) похож на эхо-сеть, но есть существенное отличие: сигмоидная активация заменена пороговой функцией, а каждый нейрон является накопительной ячейкой памяти. Таким образом, при обновлении нейрона его значение не становится равным сумме соседей, а прибавляется само к себе, и при достижении порога сообщается другим нейронам.
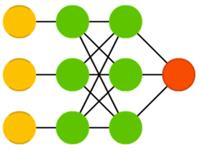
Метод опорных векторов(support vector machines, SVM) находит оптимальные решения задачи оптимизации. Классическая версия способна категоризировать линейно разделяемые данные: например, различать изображения с котом Томом и с котом Гарфилдом. В процессе обучения сеть как бы размещает все данные на 2D-графике и пытается разделить данные прямой линией так, чтобы с каждой стороны были данные только одного класса и чтобы расстояние от данные до линии было максимальным. Используя трюк с ядром, можно классифицировать данные размерности n. Что характерно, этот метод не всегда рассматривается как нейронная сеть.
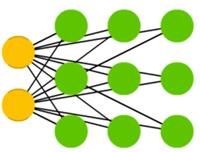
И наконец, нейронные сети Кохонена(Kohonen networks, KN), также известные каксамоорганизующиеся карты(self organising (feature) maps, SOM, SOFM), завершают наш список. Эти сети используют соревновательное обучение для классификации данных без учителя. Сети подаются входные данные, после чего сеть определяет, какие из нейронов максимально совпадают с ними. После этого эти нейроны изменяются для ещё большей точности совпадения, в процессе двигая за собой соседей. Иногда карты Кохонена также не считаются нейронными сетями.
Теперь вы будете разбираться в видах нейронных сетей
Сеть Хопфилда
Данная модель, видимо, является наиболее распространенной математической моделью в нейронауке. Это обусловлено ее простотой и наглядность. Сеть Хопфилда показывает, каким образом может быть организована память в сети из элементов, которые не являются очень надежными. Экспериментальные данные показывают, что при увеличении количества вышедших из строя нейронов до 50%, вероятность правильного ответа крайне близка к 100%.
Джон Хопфилд впервые представил свою ассоциативную сеть в 1982 г. в Национальной Академии Наук. В честь Хопфилда и нового подхода к моделированию, эта сетевая парадигма упоминается как сеть Хопфилда. Сеть базируется на аналогии физики динамических систем. Начальные применения для этого вида сети включали ассоциативную, или адресованную по смыслу память и решали задачи оптимизации.
Сеть Хопфилда является однослойной сетью (хотя иногда для удобства в ней выделяют три слоя - входной, слой Хопфилда и выходной слой), потому что в ней используется лишь один слой нейронов. Она так же является рекурсивной сетью, потому что обладает обратными связями. Она функционирует циклически. Сеть состоит из N искусственных нейронов, аксон каждого нейрона связан с дендритами остальных нейронов, образуя обратную связь.
Пример сети Хопфилда из трёх нейронов. Каждый из них имеет выходы сигнала, который подаются на входы всех остальных нейронов, кроме себя самого:
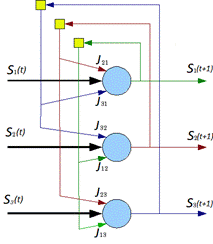
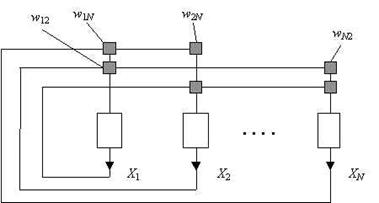
Однако эту сеть нельзя научить практически ничему. Нам нужно намного больше нейронов. Сеть, содержащая N нейронов может запомнить не более ~0.15*N образов (точнее – 0.14). Так что реальная сеть должна содержать достаточно внушительное количество нейронов. Это одно из существенных недостатков сети Хопфилда – небольшая ёмкость. Плюс ко всему образы не должны быть очень похожи друг на друга, иначе в некоторых случаях возможно зацикливание при распознавании.
Как работает сеть. Основным ее применением является восстановление образца, ранее сохраненного сетью, по подаваемому на ее вход искаженному образцу. Образ, который сеть запоминает или распознаёт (любой входной образ) может быть представлен в виде вектора X размерностью n, где n – число нейронов в сети. Выходной образ представляется вектором Y с такой же размерностью. Каждый элемент вектора может принимать значения: +1 либо -1 (Можно свести к 0 и 1, однако +1 и -1 удобнее для расчётов). каждая связь характеризуется своим весом wij , матрица весов предполагается симметричной: wji = wij (N >> 1).
ОБУЧЕНИЕ:
Алгоритм обучения сети Хопфилда существенно отличается от таких классических алгоритмов обучения перцептронов, как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе.
На стадии инициализации сети синаптические коэффициенты устанавливаются таким образом:
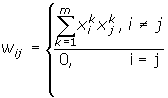
Здесь i и j - индексы, соответственно, предсинаптического (приёмник сигнала) и постсинаптического (источник сигнала) нейронов; xki, xkj - i-ый и j-ый элементы вектора k-ого образца.
Симметричность матрицы w (wij = wji) и наличие нулей в случае i=j обусловлено требованием устойчивости, поскольку сеть с обратными связями является устойчивой, если её матрица симметрична и имеет нули на главной диагонали [Cohen M. A., Grossberg S. G. 1983]
Если нам необходимо дообучить уже обученную на k образцах нейронную сеть новому k+1 образцу, мы просто прибавляем к каждому синаптическому коэффициенту wji произведение соответствующих элементов вектора xk+1 : wji = wji + xk+1i * xk+1j .
РАСПОЗНАВАНИЕ:
В режиме функционирования, сеть направляет данные с входных дендритов через фиксированные веса соединений к нейронам сети (слою Хопфилда). Слой колеблется до тех пор, пока не будет завершено определенное количество циклов, после чего на выходах (аксонах) нейронов получается выходное состояние. Это состояние отвечает образу, уже запрограммированному в сеть.
1. На входы сети подается неизвестный сигнал X. Его распространение непосредственно устанавливает значения выходов Y:
yi(0) = xi , i = 0...n-1,
поэтому обозначения на схеме сети входных сигналов в явном виде носит чисто условный характер. Нуль в скобке yi означает нулевую итерацию в цикле работы сети.
2. Рассчитывается новое состояние нейронов (значения источников умножаются на соответственные веса нейрона и суммируются)
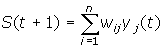 , j=0...n-1
, j=0...n-1
и новые значения выходов
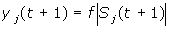
где f - активационная функция в виде скачка.
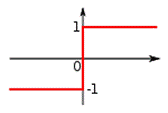
Процесс повторяется до тех пор, пока значения на выходах нейронов не стабилизируются.
Y(t+1) = Y(t)
После чего выходной вектор представляет собой образец, который наиболее соответствует входным данным.
У сети Хопфилда имеется два способа реализации:
синхронный ‑ когда состояния t+1 вычисляются сначала для всех нейронов и лишь после этого одновременно (синхронно) состояние t у всех нейронов меняется на t+1
асинхронный – после вычисления нового состояния t+1 очередного нейрона, состояния всех последующих нейронов вычисляются уже с учётом этого изменения.
Принципиальная разница между двумя режимами работы сети состоит в том, что в асинхронном случае сеть обязательно придёт к одному устойчивому состоянию. При синхронном же возможны (но отнюдь не всегда) ситуации с бесконечным циклическим переходом между двумя разными состояниями (динамический аттрактор). Поэтому синхронный режим практически для сети Хопфилда не используется, и рассматривается лишь как основа для понимания более сложного асинхронного режима.
Иногда сеть не может провести распознавания и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети.
Для сети Хопфилда число запомненных образов m не должно превышать величины, приблизительно равной m= N / (2 log2N) или 0.15*N. Попытка записи бо́льшего числа образов приводит к тому, что нейронная сеть перестаёт их распознавать.
Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызвать в сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.
Сеть Хэмминга
Сеть Хемминга – это одна из наиболее многообещающих распознающих и классифицирующих нейронных сетей. Она используется для решения задач классификации бинарных входных векторов. В основе ее работы лежат процедуры, направленные на выбор в качестве решения задачи классификации одного из эталонных образов, наиболее близкого к поданному на вход сети зашумленному входному образу, и отнесение данного образа к соответствующему классу (черно-белые изображения представляются в виде m-мерных биполярных векторов). Свое название она получила от расстояния Хемминга (количество различающихся переменных у зашумленного и эталонного входных образов), которое используется в сети в качестве критерия оценки меры близости к каждому классу сходства R изображений входного и эталонных, хранимых с помощью весов связей сети.
Сеть используется для того, чтобы соотнести бинарный вектор x = (x1, x2, x3, … xm), где xi = {-1,1} с одним из эталонных образов (каждому классу соответствует свой образ), или же решить, что вектор не соответствует ни одному из эталонов. В отличии от сети Хопфилда, выдаёт не сам образец, а его номер.
Сеть предложена Ричардом Липпманном в 1987 году. Она позиционировалась как специализированное гетероассоциативное запоминающее устройство.
Мера сходства определяется соотношением
R = m – Rx, где
m – число компонент входного и эталонных векторов;
Rx - расстояние Хемминга между векторами.
Определение: Расстоянием Хемминга 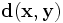 между двумя двоичными векторами X и Y длины n называется число позиций, в которых векторы различны.
между двумя двоичными векторами X и Y длины n называется число позиций, в которых векторы различны.
В общем виде расстояние Хэмминга 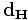 для объектов
для объектов 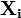 и
и 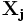 размерности
размерности 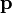 задаётся функцией:
задаётся функцией:
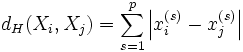
Расстояние Хэмминга обладает свойствами метрики, удовлетворяя следующим условиям:
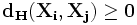
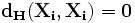
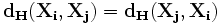
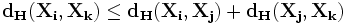
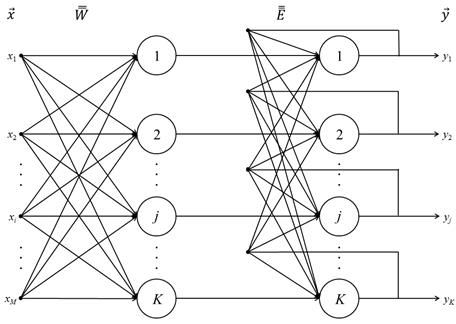
Сеть Хэмминга — трёхслойная нейронная сеть (один слой входной и два классифицирующих) с обратной связью.
Общая постановка задачи, которая решается с помощью нейронной сети Хэмминга, следующая. Имеется исходный набор эталонных образов, представленных в виде бинарных векторов. Каждому из них соответствует свой класс. Требуется для поданного на входы сети неизвестного образа произвести его сопоставление со всеми известными эталонными образами и отнесение к соответствующему классу либо сделать заключение о несоответствии ни одному из классов.
Количество нейронов во втором и третьем слоях равно K ‑ количеству классов классификации. Синапсы нейронов второго слоя соединены с каждым входом сети, нейроны третьего слоя связаны между собой отрицательными связями, кроме синапса, связанного с собственным аксоном каждого нейрона — он имеет положительную обратную связь.
Число входов M соответствует числу бинарных признаков, по которым различаются образы. Значения входных переменных принадлежат множеству {–1; 1}. Выходные значения подаются по обратным связям на входы нейронов второго слоя, в том числе свой собственный.
ОБУЧЕНИЕ:
На стадии обучения выполняется следующая последовательность действий:
1. Формируется матрица эталонных образов 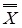
 размера K x M (табл. 1)
размера K x M (табл. 1)
Таблица 1. Матрица эталонных образов нейронной сети Хэмминга
| №образа | № входной бинарной переменной | |||||
| … | i | … | M | |||
| x11 | x12 | … | x1i | … | x1M | |
| x21 | x22 | … | x2i | … | x2M | |
| … | … | … | … | … | … | … |
| j | xj1 | xj2 | … | xji | … | xjM |
| … | … | … | … | … | … | … |
| K | xK1 | xK2 | … | xKi | … | xKM |
2. Рассчитывается матрица весовых коэффициентов нейронов первого слоя:
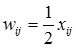 или в матричной форме записи:
или в матричной форме записи: 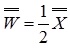
 .
.
3. Определяются настройки активационной функции:
– вид – линейная пороговая функция:
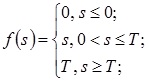
– параметр:
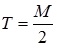

Таким образом, очевидно, что выходы нейронной сети могут принимать любые значения в пределах [0, T].
4. Задаются значения синапсов обратных связей нейронов второго слоя в виде элементов квадратной матрицы размераK x K:
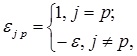 где
где 
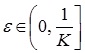
или в матричной форме:

 Синапсы обратных связей нейронной сети Хэмминга, имеющие отрицательный вес, называются ингибиторными, или тормозящими.
Синапсы обратных связей нейронной сети Хэмминга, имеющие отрицательный вес, называются ингибиторными, или тормозящими.
5. Устанавливается максимально допустимое значение нормы разности выходных векторов на двух последовательных итерациях Emax, требующееся для оценки стабилизации решения. Обычно достаточно принимать Emax = 0,1.
РАСПОЗНАВАНИЕ:
На стадии практического использования выполняются следующие действия:
1. На входы сети подается неизвестный, в общем случае, зашумленный вектор сигналов 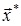 .
.
2. Рассчитываются состояния и выходные значения нейронов первого слоя.
Для расчета состояний нейронов используется соотношение:
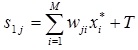
 или в матричной форме:
или в матричной форме: 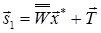

Для расчета выходов нейронов первого слоя 
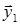 к полученным значениям состояний применяется активационная функция f(s).
к полученным значениям состояний применяется активационная функция f(s).
3. Выходам нейронов второго слоя в качестве начальных величин присваиваются значения выходов нейронов первого слоя, полученные на предыдущем шаге:
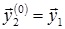
 .
.
Далее первый слой нейронов на стадии практического использования больше не задействуется.
4. Для каждой итерации q рассчитываются новые значения состояний и выходов нейронов второго слоя.
Состояния нейронов определяются по соотношению:

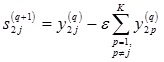 или в матричной форме записи:
или в матричной форме записи: 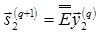

Новые выходные значения 
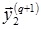 определяются в результате применения линейной пороговой активационной функции (2) к соответствующим состояниям нейронов
определяются в результате применения линейной пороговой активационной функции (2) к соответствующим состояниям нейронов 
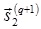 .
.
5. Цикл в п.4 повторяется до стабилизации выходного вектора в соответствии с условием:
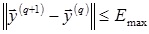

В идеальном случае после стабилизации должен получиться выходной вектор с одним положительным и всеми остальными нулевыми элементами. Индекс единственного положительного элемента непосредственно указывает на класс неизвестного входного образа.
Если данные входного образа сильно зашумлены или в обучающей выборке отсутствовал подходящий эталон, в результате остановки цикла в п..4 могут быть получены несколько положительных выходов, причем значение любого из них окажется меньше, чем Emax. В этом случае делается заключение о невозможности отнесения входного образа к определенному классу, однако индексы положительных выходов указывают на наиболее схожие с ним эталоны.
Дата добавления: 2016-12-27; просмотров: 4254;











