Обучение нейронных сетей
Нейронные сети используются для представления знаний. В отличие от обычного вычисления представление знания в нейронных сетях выполняет поиск по содержанию, а не по адресу сохраненных данных. Кроме того, представление знаний в нейронных сетях осуществляется через приблизительное, а не абсолютно точное соответствие. Представление знаний в нейронных сетях состоит из сети, весов связей и семантических интерпретаций, присоединенных к активациям узлов. Например, в контексте управленческой классификации при использовании обученной нейронной сети можно предугадать, выберет ли клиент новый продукт, основываясь на выраженных в числах данных о клиенте, таких как последняя купленная марка, интерес к предварительному экспонированию, возможность дополнительного экспонирования и интерес к нему. Эти кванторные признаки атрибутов являются входами в обученную нейронную сеть. Активация «+1», полученная от нейронной сети, может указывать на то, что клиент выберет новое изделие, а «-1» — наоборот.
Обобщение знаний в нейронных сетях достигается путем обучения. Процесс обучения в нейронных сетях стимулирует желательные образцы активации и блокирует нежелательные, основываясь на доступных данных. Для достижения определенного обобщения знаний в нейронной сети разрабатывается алгоритм обучения. Функция ошибки, определенная на выходе нейронной сети, или энергетическая функция, определенная при активации элементов сети, характеризует качество нейронной сети в обобщении знаний. Обучающий набор данных в этом случае должен состоять из образцов представления знаний, которым предполагается обучить нейронную сеть. Алгоритм обучения действует методом изменения либо весов (т. е. силы связей между узлами), либо выходов нейронной сети, либо структуры нейронной сети, стремясь к минимальным ошибкам или энергии, основываясь на обучающих данных.
В системах нейронных сетей большое количество парадигм обучения. Обучение с учителем (контролируемое обучение) и обучение без учителя (неконтролируемое обучение или самообучение) — вот две главные парадигмы, обычно используемые в проектировании обучающих алгоритмов. Бывает ещё смешанная парадигма.
В парадигме обучения с учителем нейронная сеть располагает правильными ответами (выходами сети) на каждый входной пример. Процесс обучения пытается минимизировать «дистанцию» между фактическими и желаемыми выходами нейронной сети. Веса настраиваются так, чтобы сеть производила ответы как можно более близкие к известным правильным ответам. Усиленный вариант обучения с учителем предполагает, что известна только критическая оценка правильности выхода нейронной сети, но не сами правильные значения выхода.
Противоположностью обучения с учителем является обучение без учителя. В отличие от обучения с учителем здесь не существует априорного набора желаемых значений выхода и не требуется знания правильных ответов на каждый пример обучающей выборки. Когда используется такая парадигма, подразумевается несколько образцов входа. Предполагается, что в процессе обучения нейронная сеть обнаруживает существенные особенности входов (раскрывается внутренняя структура данных или корреляции между образцами в системе данных, что позволяет распределить образцы по категориям). Нейронная сеть должна развить собственное представление стимулов входа без помощи учителя.
При смешанном обучении часть весов определяется посредством обучения с учителем, в то время как остальная получается с помощью самообучения.
Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность.
Под емкостью понимается, сколько образцов может запомнить сеть, и какие функции и границы принятия решений могут быть на ней сформированы.
Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению. Слишком малое число примеров может вызвать "переобученность" сети, когда она хорошо функционирует на примерах обучающей выборки, но плохо - на тестовых примерах, подчиненных тому же статистическому распределению.
Известны 4 основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования.
Правило коррекции по ошибке. При обучении с учителем для каждого входного примера задан желаемый выход d. Реальный выход сети y может не совпадать с желаемым. Принцип коррекции по ошибке при обучении состоит в использовании сигнала (d-y) для модификации весов, обеспечивающей постепенное уменьшение ошибки. Обучение имеет место только в случае, когда перцептрон ошибается. Известны различные модификации этого алгоритма обучения [J. Hertz, A. Krogh, and R.G. Palmer, Introduction to the Theory of Neural Computation, Addison-Wesley, Reading, Mass., 1991].
Обучение Больцмана. Представляет собой стохастическое правило обучения, которое следует из информационных теоретических и термодинамических принципов [J.A. Anderson and E. Rosenfeld, "Neurocomputing: Foundation of Research", MIT Press, Cambridge, Mass., 1988.]. Целью обучения Больцмана является такая настройка весовых коэффициентов, при которой состояния видимых нейронов удовлетворяют желаемому распределению вероятностей. Обучение Больцмана может рассматриваться как специальный случай коррекции по ошибке, в котором под ошибкой понимается расхождение корреляций состояний в двух режимах.
Правило Хебба. Самым старым обучающим правилом является постулат обучения Хебба [D.O. Hebb, The Organization of Behavior, John Wiley & Sons, New York, 1949.]. Хебб опирался на следующие нейрофизиологические наблюдения: если нейроны с обеих сторон синапса активизируются одновременно и регулярно, то сила синаптической связи возрастает. Важной особенностью этого правила является то, что изменение синаптического веса зависит только от активности нейронов, которые связаны данным синапсом. Это существенно упрощает цепи обучения в реализации VLSI.
Обучение методом соревнования. В отличие от обучения Хебба, в котором множество выходных нейронов могут возбуждаться одновременно, при соревновательном обучении выходные нейроны соревнуются между собой за активизацию. Это явление известно как правило "победитель берет все". Подобное обучение имеет место в биологических нейронных сетях. Обучение посредством соревнования позволяет кластеризовать входные данные: подобные примеры группируются сетью в соответствии с корреляциями и представляются одним элементом.
При обучении модифицируются только веса "победившего" нейрона. Эффект этого правила достигается за счет такого изменения сохраненного в сети образца (вектора весов связей победившего нейрона), при котором он становится чуть ближе ко входному примеру. На рис. 3 дана геометрическая иллюстрация обучения методом соревнования. Входные векторы нормализованы и представлены точками на поверхности сферы. Векторы весов для трех нейронов инициализированы случайными значениями. Их начальные и конечные значения после обучения отмечены Х на рис. 3а и 3б соответственно. Каждая из трех групп примеров обнаружена одним из выходных нейронов, чей весовой вектор настроился на центр тяжести обнаруженной группы.
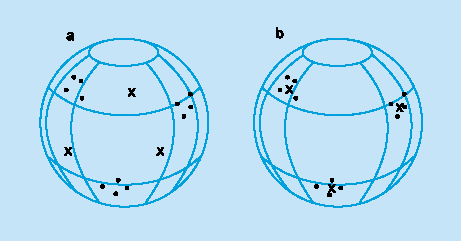
Рис. N.Пример обучения методом соревнования: (а) перед обучением; (б) после обучения
Можно заметить, что сеть никогда не перестанет обучаться, если параметр скорости обучения не равен 0. Некоторый входной образец может активизировать другой выходной нейрон на последующих итерациях в процессе обучения. Это ставит вопрос об устойчивости обучающей системы. Система считается устойчивой, если ни один из примеров обучающей выборки не изменяет своей принадлежности к категории после конечного числа итераций обучающего процесса. Один из способов достижения стабильности состоит в постепенном уменьшении до 0 параметра скорости обучения. Однако это искусственное торможение обучения вызывает другую проблему, называемую пластичностью и связанную со способностью к адаптации к новым данным. Эти особенности обучения методом соревнования известны под названием дилеммы стабильности-пластичности Гроссберга.
В Таблице 2 представлены различные алгоритмы обучения и связанные с ними архитектуры сетей (список не является исчерпывающим). В последней колонке перечислены задачи, для которых может быть применен каждый алгоритм. Каждый алгоритм обучения ориентирован на сеть определенной архитектуры и предназначен для ограниченного класса задач. Кроме рассмотренных, следует упомянуть некоторые другие алгоритмы:
Adaline и Madaline [R.P.Lippmann, "An Introduction to Computing with Neural Nets", IEEE ASSP Magazine, Vol.4, No.2, Apr. 1987, pp. 4-22.],
линейный дискриминантный анализ], проекции Саммона [A.K. Jain and J. Mao, "Neural Networks and Pattern Recognition", in Computational Intelligence: Imitating Life, J.M. Zurada, R.J. Marks II, and C.J. Robinson, eds., IEEE Press, Piscataway, N.J., 1994, pp. 194-212.],
метод/анализ главных компонентов [J. Hertz, A. Krogh, and R.G. Palmer, Introduction to the Theory of Neural Computation, Addison-Wesley, Reading, Mass., 1991.].
Таблица 2. Известные алгоритмы обучения.
| Парадигма | Обучающее правило | Архитектура | Алгоритм обучения | Задача |
| С учителем | Коррекция ошибки | Однослойный и многослойный перцептрон | Алгоритмы обучения перцептрона Обратное распространение Adaline и Madaline | Классификация образов Аппроксимация функций Предсказание, управление |
| Больцман | Рекуррентная | Алгоритм обучения Больцмана | Классификация образов | |
| Хебб | Многослойная прямого распространения | Линейный дискриминантный анализ | Анализ данных Классификация образов | |
| Соревнование | Соревнование | Векторное квантование | Категоризация внутри класса Сжатие данных | |
| Сеть ART | ARTMap | Классификация образов | ||
| Без учителя | Коррекция ошибки | Многослойная прямого распространения | Проекция Саммона | Категоризация внутри класса Анализ данных |
| Хебб | Прямого распространения или соревнование | Анализ главных компонентов | Анализ данных Сжатие данных | |
| Сеть Хопфилда | Обучение ассоциативной памяти | Ассоциативная память | ||
| Соревнование | Соревнование | Векторное квантование | Категоризация Сжатие данных | |
| SOM Кохонена | SOM Кохонена | Категоризация Анализ данных | ||
| Сети ART | ART1, ART2 | Категоризация | ||
| Смешанная | Коррекция ошибки и соревнование | Сеть RBF | Алгоритм обучения RBF | Классификация образов Аппроксимация функций Предсказание, управление |
Дата добавления: 2016-12-27; просмотров: 6224;











