Транзитивное замыкание нечетких отношений

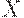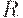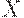Большое значение в приложениях теории нечетких отношений играют транзитивные отношения. Они обладают многими удобными свойствами и определяют некоторую правильную структуру множества . Например, если отношение в характеризует сходство между объектами, то транзитивность такого отношения обеспечивает возможность разбиения множества 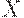на непересекающиеся классы сходства. Если же отношению в 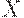придать смысл "предпочтения" или "доминирования", тотранзитивность такого отношения обеспечивает возможность естественного упорядочения объектов множества 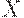, существование "наилучших", "недоминируемых" объектов и т.п. Поэтому представляет большой интерес возможность преобразования исходного нетранзитивного отношения в транзитивное. Такое преобразование обеспечивает операциятранзитивного замыкания нечеткого отношения.

Транзитивным замыканием отношения 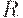называется отношение 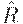, определяемое следующим образом:

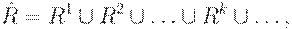
где отношения 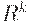определяются рекурсивно:

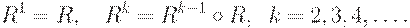
Теорема. Транзитивное замыкание 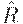любого нечеткого отношения 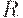транзитивно и является наименьшим транзитивным отношением, включающим 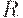, т.е. 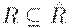, и для любого транзитивного отношения 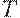, такого, что 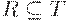, следует .

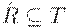Как следствие из данной теоремы получаем, что 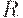транзитивно тогда и только тогда, если .

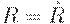Если множество 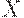содержит 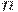элементов, то имеем

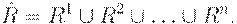
В случае, когда 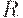рефлексивно, имеем

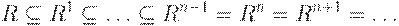
Весьма полезным фактором является то, что 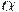-уровень транзитивного замыкания нечеткого отношения 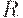совпадает странзитивным замыканием соответствующего 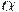-уровня:

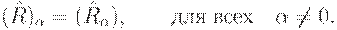
Заметим, что при транзитивном замыкании нечеткого отношения 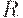в общем случае сохраняются лишь некоторые свойства отношения 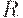. Такими свойствами являются рефлексивность, симметричность, линейность и транзитивность.