Определение конечной температуры проводника при КЗ


Конечная температура проводника при КЗ определяется аналитически при следующих допущениях:

• процесс нагревания проводника считается адиабатическим;

• зависимость удельного сопротивления проводника от температуры принимается линейной;

• удельная теплоёмкость материала проводника принимается не зависящей от температуры;

• распределение тока КЗ по сечению проводника принимается равномерным.

Процесс нагревания проводника при КЗ описывается дифференциальным уравнением: ,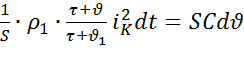

где i- полный ток КЗ; 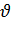- текущее значение температуры проводника в переходном процессе; 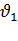- начальная температура проводника; 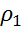- удельное сопротивление материала проводника при начальной температуре; S – сечение проводника; С – удельная теплоёмкость материала проводника. Левая часть равенства это энергия, выделившаяся в проводнике заданного сечения на длине 1 м в течение времени dt при температуре 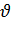; правая часть – энергия поглощаемая проводником при повышении его температуры d 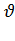. Для определения конечной температуры проводника следует разделить переменные и интегрировать левую часть в пределах от нуля до 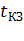, а правую часть от 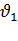до . 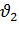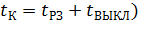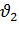( - конечная температура проводника.

.

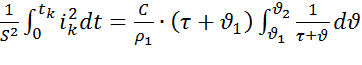Начальную температуру 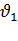принимаем равной нулю, тогда после интегрирования имеем: ,

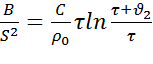где В= 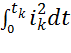- интеграл Джоуля, А2 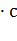; В/S2=A – интеграл квадратичной плотности тока КЗ, А2 с/м4.

По данному выражению строятся зависимости конечной температуры проводника от квадратичной плотности тока КЗ (рисунок 21).

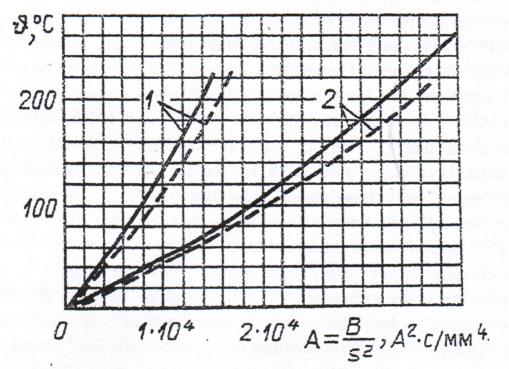
Рисунок 21. Кривые для определения конечной температуры проводников при КЗ: 1 – алюминий, 2 – медь. Сплошные линии – шины, пунктир – кабели.

12. Электродинамические силы в токопроводах и электрических

Аппаратах

12.1 Общие правила. Из курса физики известно, что электрические токи в проводниках взаимодействуют. Силы взаимодействия проводников с током называют электродинамическими. Они пропорциональны квадрату тока и обратно пропорциональны расстоянию между ними. Эти силы взаимодействия достигают своих максимальных значений при коротких замыканиях. Им подвержены все токоведущие элементы ЭУ. Шинные конструкции, электрические аппараты, силовые и измерительные трансформаторы и т. п., должны обладать достаточной механической прочностью, чтобы противостоять действию электродинамических сил при КЗ.

Большинство токоведущих частей в ЭУ расположены параллельно или близко к этому. Силы взаимодействия притягивают, один проводник к другому если токи в них направлены в одну сторону, и отталкивают – если в разные стороны (рисунок 22)

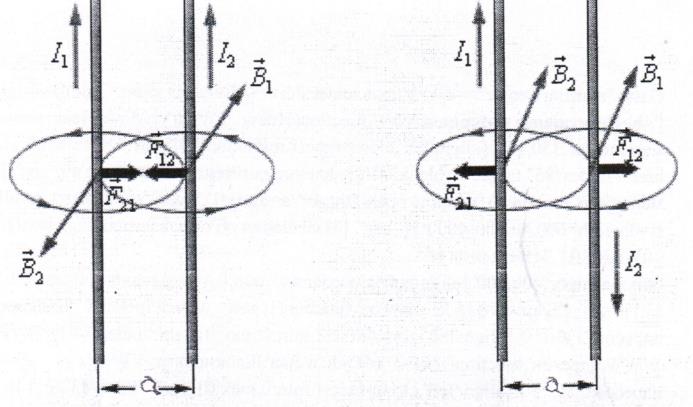
Рисунок 22. Силы взаимодействия двух проводников с током.

 

12.2 Электродинамические силы в трехфазном токопроводе при

Коротком замыкании

Взаимодействие параллельных проводников прямоугольного сечения требует введения поправочного коэффициента формы. Он может быть определен следующим образом. Проводники с током I1 и I2 разделяют на ряд элементов с бесконечно малыми поперечными сечениями. Определяют токи в них, исходя из предположения равномерного распределения тока по сечению проводника.

;

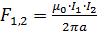где a – расстояние между проводниками; 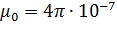- магнитная проницаемость воздуха. Найденная таким методом расчетная сила 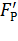является сложной функцией размеров поперечного сечения и расстояния между ними, которая может быть приведена к виду ,

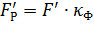где 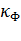- коэффициент формы. Он определяется по кривым, приведенным в справочной литературе и из рисунка 23.

 

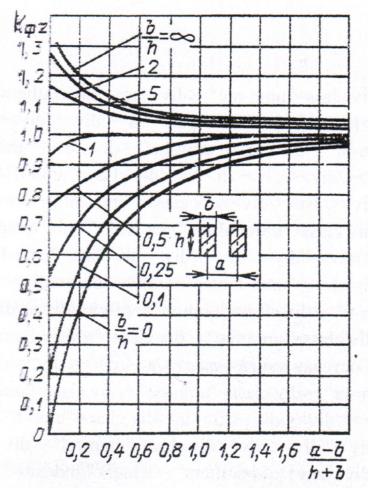
Рисунок 23. Кривые для определения коэффициента формы проводника

прямоугольного сечения.

12.3 Электродинамические силы в кольцевом проводнике.

Сила F , действующая на длине 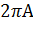кольцевого проводника, распределена равномерно по окружности (рисунок 24). Она стремиться увеличить радиус кольца, т. е. совершить работу .

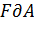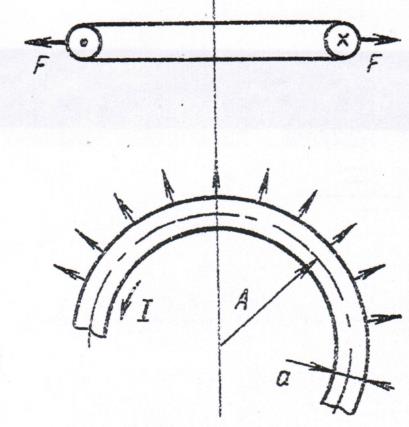
Рисунок 24. Распределение электродинамической силы в кольцевом

проводнике.

Энергия магнитного поля кольца при этом увеличивается на (I2/2) 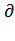L,

Где L – индуктивность кольца. Сила F может быть определена из условия

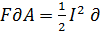L, откуда .

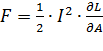При 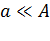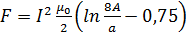или на единицу длины

.

Это выражение может быть использовано при расчете электродинамических сил в многослойных катушках электрических аппаратов.

 

12.4 Электродинамические силы в трёхфазном токопроводе при КЗ

Электродинамические силы в проводниках зависят от вида КЗ, периодической составляющей тока, постоянной времени затухания апериодической составляющей и от фазы включения – угла 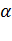, определяющего фазу напряжения в момент КЗ. Фаза включения 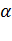должна быть выбрана так, чтобы получить наибольшее значение полного тока. Как известно это имеет место при .

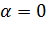При трёхфазном КЗ токи в проводниках представляются в следующем виде:

 

];

;

;

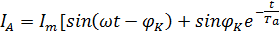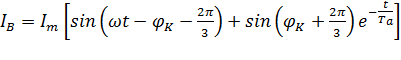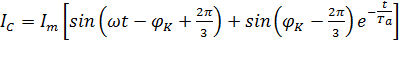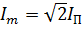- амплитуда периодической составляющей тока трёхфазного КЗ;

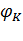= arctg X/R; 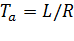– постоянная времени затухания апериодической составляющей тока КЗ.

Сила взаимодействия среднего проводника В с двумя крайними А и С при трёхфазном КЗ (рисунок 25) отнесенная к единице длины, может быть определена из выражения

.

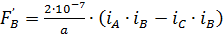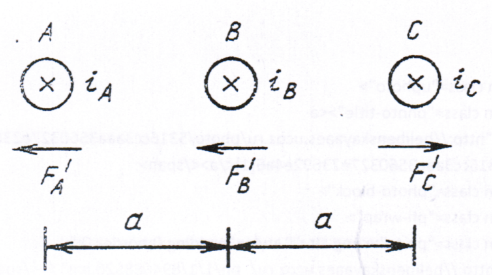
Рисунок 25. Условное направление токов и электродинамических сил в трёхфазном токопроводе при КЗ.

 

Знак минус указывает, что силы взаимодействия с крайними проводниками

А и С направлены противоположно. Силы, действующие на единицу длины крайних проводников,

.

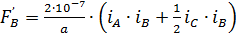Множитель ½ у второго слагаемого учитывает удвоенное расстояние между проводами А и С.

Динамическая устойчивость шинных конструкций определяется для фазы В т. к. она при КЗ находится в самых тяжёлых условиях. Наступает момент, когда фаза А притягивает фазу В, а в тоже время фаза С отталкивает фазу В, и на фазу В действуют две силы, приложенные в одну сторону. Если при расчетах оказывается, что шинная конструкция фазы В удовлетворяет требованиям механической стойкости, то фазы А и С тем более.

 

12.5 Расчёт максимальной силы действующей на проводники шинных

Конструкций

Максимальную силу 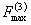, H, (эквивалентную равномерно распределенной подлине пролета нагрузки), действующую в трехфазной системе проводников на расчетную фазу при трехфазном КЗ, следует определять по формуле

,

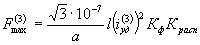где l - длина пролёта, м; 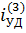- ударный ток трёхфазного КЗ, А;

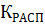– коэффициент, зависящий от взаимного расположения проводников;

КФ - коэффициент формы, (рисунок 23);

а – расстояние между проводниками, м.
Значения коэффициента Красп для некоторых типов шинных конструкций (рисунок 26) указаны в таблице. 12.1.

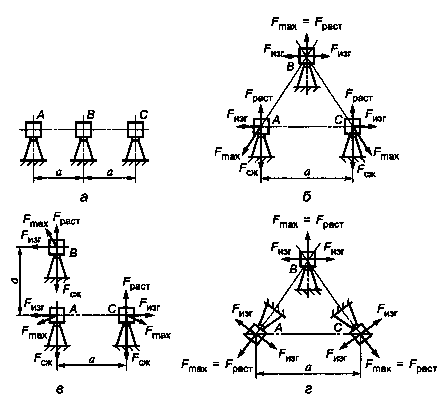
Рисунок 26. Схемы взаимного расположения шинных конструкций

Таблица 12.1 Значения коэффициента Красп

Расположение шин Расчетная фаза Значение коэффициента Kрасп для нагрузок
результирующей изгибающей растягива- ющей сжимающей
В одной плоскости (рисунок 2 а) В 1,00 1,00
По вершинам равностороннего треугольника (рисунок 2 б) А 1,00 0,94 0,25 0,75
В 1,00   1,00
С 1,00 0,94 0,25 0,75
По вершинам прямоуголь. Равнобедрен. треугольника (рисунок 2 в) А 0,87 0,87 0,29 0,87
В 0,95 0,43 0,83 0,07
С 0,95 0,93 0,14 0,43
По вершинам равностороннего треугольника, но оси изоляторов расположены под углом 2π/3 друг к другу (рисунок 2 г) А, В, С 1,00 0,50 1,00

При двухфазном КЗ максимальную силу определяют по формуле

,


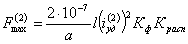Дата добавления: 2016-12-27; просмотров: 3781;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.013 сек.