ЕМКОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

В главе I § 10 был объяснен процесс заряда и разряда конденсатора, включенного в цепь постоянного тока.

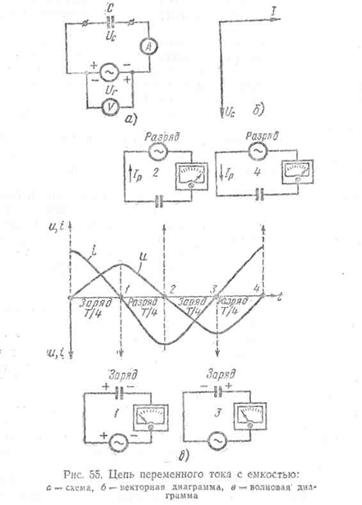
Рассмотрим теперь цепь переменного тока (рис. 55,а), в кото­рую включена электрическая емкость (конденсатор). Активным сопротивлением этой цепи пренебрегаем (r = 0).

Полярность зажимов генератора переменного тока, включенного в цепь с емкостью, меняется с частотой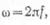

В первую четверть периода (рис. 55, в) конденсатор заряжаете и на его пластинах появляются противоположные по знаку электрические заряды (на левой пластине плюс, на правой — минус).

При заряде конденсатора по проводам, соединяющим генератор с пластинами, перемещаются электрические заряды, следовательно, протекает зарядный ток, измеряемый миллиамперметром. Через диэлектрик конденсатора ток не проходит. Как видно на волновой диаграмме, в первую четверть периода во время заряда конденса­тора напряжение на пластинах конденсатора возрастает от нуля до максимального значения, сила тока, наоборот, в начале заряда будет максимальной, а в конце заряда, когда напряжение на конден­саторе (Uс) окажется равным напряжению генератора (Ur,), она станет равной нулю.

За вторую четверть периода напряжение генератора постепенно убывает и становится равным нулю. В это время конденсатор раз­ряжается. При этом разрядный ток, протекающий по проводам, имеет направление, противоположное направлению тока заряда.

За третью четверть периода полярность на зажимах генератора изменится и напряжение возрастет от нуля до наибольшего значе­ния. В это время конденсатор вновь зарядится, но полярность на его пластинах изменится. На левой пластине будет отрицательный заряд, на правой — положительный заряд. По проводам пройдет за­рядный ток, сила которого к концу заряда конденсатора, когда Uс = Ur, станет равной нулю.

В четвертую часть периода напряжение генератора убывает и становится равным нулю. Конденсатор в это время вторично разря­жается, и по проводам, соединяющим генератор с пластинами кон­денсатора, вновь протекает разрядный ток.

Из сказанного следует, что за один период изменения перемен­ного напряжения дважды происходит процесс заряда и разряда конденсатора и при этом в его цепи протекает переменный ток. Кроме того, при заряде и разряде конденсатора ток в цепи и напря­жение не совпадают по фазе. Ток опережает по фазе напряжение на четверть периода, т. е. на 90°.

Построим векторную диаграмму для цепи переменного тока с емкостью (рис. 55, б). Для этого отложим вектор тока I в выбран­ном масштабе по горизонтали. Чтобы на векторной диаграмме по­казать, что напряжение отстает от тока на угол  = 90°, отклады­ваем вектор напряжения Uс вниз под углом 90°.

Выясним, от чего зависит сила тока в цепи с емкостью. Обозна­чим сопротивление цепи Хс и назовем его емкостным сопротивле­нием. Тогда закон Ома для цепи с емкостью можно выразить так:

где U —напряжение генератора, в;

Хc — емкостное сопротивление, ом;

I — сила тока, а.

Известно, что сила тока в цепи определяется количеством элек­трических зарядов, проходящих через поперечное сечение провод­ника в единицу времени:

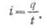
Если в единицу времени по проводам протекает большое количество зарядов, то сила тока будет большой, и наоборот, когда по проводам в каждую секунду протекает малое количество зарядов,
то сила тока оказывается незначительной.

Допустим, что частота переменного тока, вырабатываемого генератором, большая. В этом случае в каждую секунду конденсатор много раз (часто) заряжается и разряжается. В проводах, идущих от генератора к пластинам конденсатора, будет перемещаться в каждую секунду большое количество электрических зарядов. По этому можно сказать, что в рассматриваемой цепи возникает боль­шая сила тока и в данном случае, согласно закону Ома, емкостное сопротивление цепи Хс оказывается малой величиной.

Если же частота переменного тока генератора будет мала, то конденсатор в каждую секунду зарядится и разрядится меньшее количество раз: В связи с этим по проводам цепи в каждую секунду пройдет незначительное количество зарядов и сила тока будет мала, а следовательно, емкостное сопротивление цепи, наоборот, будет большим.

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально частоте переменного тока.

Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь.

Допустим, что в цепь включен конденсатор большой емкости. Количество электричества, которое накапливает конденсатор при заряде и отдает при разряде, прямо пропорционально его емкости:

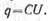
Чем больше емкость конденсатора, включенного в цепь перемен­ного тока, тем большее количество электричества переместится при заряде и разряде, по проводам, идущим от генератора к его пластинам. Поэтому в проводах возникает ток большой силы и в данном случае, согласно закону Ома, емкостное сопротивление цепи Хc будет мало. Если же включенная в цепь емкость мала, то при заряде и разряде по проводам пройдет меньшее количество электрических зарядов и сила тока будет незначительной, следовательно, емкостное сопротивление цепи, наоборот, будет большим.

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.

Таким образом. емкостное сопротивление:

где Хс — емкостное сопротивление, ом;

ώ - угловая частота переменного тока, рад/сек;

С —емкость, ф.

Известно, что угловая частота 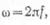. Поэтому емкостное сопротивление можно определить так:

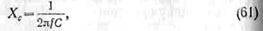
где f— частота переменного тока, гц.

Если включенная емкость измеряется в микрофарадах, то ем­костное сопротивление

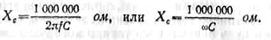
Если емкость измеряется в пикофарадах, то

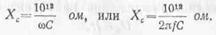
Следует подчеркнуть, что имеется существенное различие меж­ду емкостным и активным сопротивлениями. Как известно, актив­ная нагрузка безвозвратно потребляет энергию генератора пере­менного тока.

Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде кон­денсатора.

Следовательно, емкостная нагрузка не потребляет энергию ге­нератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.

Пример. Конденсатор емкостью С=2 мкф включен в цепь переменного тока, частота которого 50 гц. Определить:

1) его емкостное сопротивление при частоте f=50 гц;

2) емкостное сопротивление этого конденсатора переменному току, частота которого 500 гц.

Решение. Емкостное сопротивление конденсатора переменному току при частоте f=50 гц

При частоте f=500 гц

Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изме­няется, конденсатор практически обладает бесконечно большим со­противлением и поэтому он постоянного тока не пропускает.