ПОНЯТИЕ ОБ ЭЛЕКТРОННОЙ ТЕОРИИ СТРОЕНИЯ ВЕЩЕСТВА 2 глава
·
· 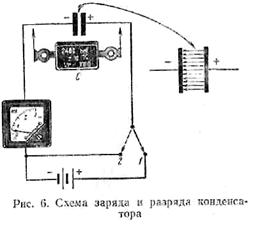 Процесс заряда конденсатора(рис. 6). При установке ключа на контакт 1 пластины конденсатора окажутся подключенными к батарее и на них появятся противоположные по знаку электрические заряды («+» и «—»). Произойдет заряд конденсатора и между его пластинами возникнет электрическое поле. При заряде конденсатора свободные электроны правой пластины переместятся по проводнику в направлении положительного полюса батареи и на этой пластине останется недостаточное количество электронов, в результате чего она приобретет, положительный заряд.
Процесс заряда конденсатора(рис. 6). При установке ключа на контакт 1 пластины конденсатора окажутся подключенными к батарее и на них появятся противоположные по знаку электрические заряды («+» и «—»). Произойдет заряд конденсатора и между его пластинами возникнет электрическое поле. При заряде конденсатора свободные электроны правой пластины переместятся по проводнику в направлении положительного полюса батареи и на этой пластине останется недостаточное количество электронов, в результате чего она приобретет, положительный заряд.
· Свободные электроны с отрицательного полюса батареи переместятся на левую пластину конденсатора и на ней появится избыток электронов — отрицательный заряд.
· Таким образом, в проводах, соединяющих пластины конденсатора с батареей, будет протекать электрический ток. Если между конденсатором и батареей не включено большое сопротивление, то время заряда конденсатора очень мало и ток в проводах протекает кратковременно.
· При заряде конденсатора энергия, сообщаемая батареей, переходит в энергию электрического поля, возникающего между пластинами конденсатора.
· Процесс разряда конденсатора (см. рис. 6). Если ключ установить на контакт 2, пластины заряженного конденсатора окажутся соединенными между собой. При этом произойдет разряд конденсатора и исчезнет электрическое поле между его пластинами.
· При разряде конденсатора избыточные электроны с левой пластины переместятся по проводам к правой пластине, где их недостает; когда количество электронов на пластинах конденсатора станет одинаковым, процесс разряда закончится и ток в проводах исчезнет.
· Энергия электрического поля конденсатора при его разряде расходуется на работу, связанную с перемещением зарядов,— на создание электрического тока.
· Время разряда конденсатора через провода, обладающие малым сопротивлением,также весьма мало.
· Процесс заряда и разряда конденсатора широко используется в различных устройствах.
· Наиболее широко распространены бумажные, слюдяные и электролитические конденсаторы постоянной ёмкости.
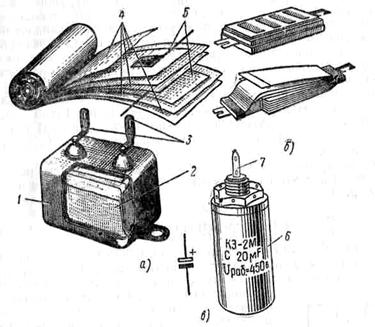
· Бумажный конденсатор КБГ. Бумажный конденсатор (рис.7) представляет собой металлический корпус 1, в котором герметически закрыт пакет 2, состоящий из пластин, выполненных в виде алюминиевой фольги 2 и изолированных одна от другой тонкой бумагой 4, пропитанной изоляционным материалом (церезином, головаксом). Пластины конденсатора присоединяются к выводным лепесткам 3, изолированным от корпуса.
· Слюдяной конденсатор КСО. Слюдяной конденсатор (рис. 7, б) состоит из двух пакетов металлических пластин и слюдяных прокладок. Между каждой парой пластин, принадлежащих разным пакетам, помещается тонкая прокладка из слюды. Собранные таким образом конденсаторы запрессовываются в пластмассу, из которой выходят наружу два лепестка по одному от каждого пакета пластин. Они служат для включения конденсатора в схему.
· Электролитический конденсатор КЭ-2М. Электролитический конденсатор (рис. 7, в) представляет собой алюминиевый стакан 6, в котором помещаются две алюминиевые ленты, скатанные в рулон. Между лентами проложена фильтровальная бумага, пропитанная электролитом.. Одна алюминиевая лента соединяется с корпусом стакана, а вторая -—с контактом 7, укрепленным на его верхней крышке. При заряде конденсатора на поверхности алюминиевых лент, подключаемых к положительному полюсу источника тока, образуется пленка окиси алюминия, являющаяся диэлектриком. Так как эта пленка очень тонкая, то емкость электрических кондесаторов относительно велика. Электролитические конденсаторы изготовляют емкостью до 2000 мкф при рабочем напряжении до 500 в.
· 
·
· Рис 7 Конденсаторы постоянной емкости:
· а-бумажный КБГ, б-слюдяной КСО, в - электролитический КЭ-2М и его условное обозначение
· 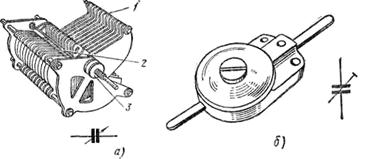
· Рис 8 Конденсаторы переменной (а) и полупеременной (б)
· емкости и их условное обозначение:
· 1 — ротор, 2 — статор, 3 — гайка крепления
·
· Конденсаторы переменной емкости. Конденсаторы, емкость которых можно изменять, называются конденсаторами переменной емкости (рис. 8, а). Такой конденсатор состоит из неподвижных пластин (статора) и подвижных пластин (ротора), укрепленных на оси. При плавном повороте оси подвижные пластины в большей или меньшей степени входят в промежутки между неподвижными пластинами, не касаясь их, и емкость конденсатора плавно увеличивается. Когда подвижные пластины полностью входят в промежутки между неподвижными пластинами, емкость конденсатора достигает наибольшей величины.
· Разновидностью конденсатора переменной емкости является конденсатор полупеременной емкости (рис. 8, б). Такой конденсатор имеет неподвижную (статор) и подвижную (ротор) пластины. Основание пластин изготовлено из керамики, а на него нанесен слой серебра.
· Ротор укреплен с помощью винта. Поворачивая винт, перемещают ротор и при этом изменяется емкость конденсатора в пределах 2—30 пф.
·
· §11. СОЕДИНЕНИЯ КОНДЕНСАТОРОВ
·
· Если необходимо увеличить общую емкость конденсаторов, то их соединяют между собой параллельно (рис. 9, а). При этом способе соединения общая площадь пластин увеличивается по сравнению с площадью пластины каждого конденсатора. Общая емкость конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов и вычисляется по формуле
· Собщ=С1 + С2+С3+ ••• (10)
· Это можно подтвердить следующим образом.
·  Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q1, q2, q3, и т. д. Следовательно,
Соединенные параллельно конденсаторы находятся под одним и тем же напряжением, равным U вольт, а общий заряд этих конденсаторов равен q кулонов. При этом каждый конденсатор соответственно получает заряд q1, q2, q3, и т. д. Следовательно,
· qобщ = q1 + q2 + q3 + •••
·
· Из формулы (8) вытекает, что заряд
· qобщ = Собщ U (11)
·
· а заряды q1 = С1U; q2 = С2U; q3 = С3U.
·
· Подставив эти выражения в формулу (11), получим:
· Собщ U= С1U + С2U + С3U.
· Разделив левую и правую части этого равенства на равную для всех конденсаторов величину U, после сокращения найдем:
· Собщ = С1 + С2 + С3
·
· Пример. Три конденсатора емкостью С1=2 мкф; C2=0,1 мкф и C3=0,5 мкф соединены параллельно.
· Вычислить их общую емкость.
· Решение.
· Собщ = С1 + С2 + С3 =2+00,1+0,5=2,6 мкф.
·
· Общую емкость конденсаторов, имеющих одинаковую емкость и соединенных параллельно, можно вычислить по формуле
· Собщ = Сn, (12)
· где С — емкость одного конденсатора,
· n — число конденсаторов.
·
· Пример. Пять конденсаторов емкостью 2 мкф каждый соединены параллельно. Определить их общую емкость.
· Решение.
· Собщ = Сn =25=10 мкф.
·
· Конденсаторы соединяют последовательно (рис. 9, б), когда
рабочее напряжение установки превышает напряжение, на которое рассчитана изоляция одного конденсатора. В этом случае правую пластину первого конденсатора соединяют с левой пластиной второго, правую пластину второго — с левой пластиной третьего и т. д. Общая емкость конденсаторов при таком соединении уменьшается. Величина, обратная общей емкости конденсаторов, соединенных последовательно 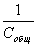 , равна сумме обратных величин емкостей отдельных конденсаторов:
, равна сумме обратных величин емкостей отдельных конденсаторов:
· 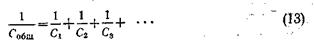
· Это можно подтвердить следующим образом. Общее напряжение на конденсаторах Uобщ а на каждом конденсаторе U1, U2, U3, тогда
· Uобщ = U1 +U2+ U3.
· Из Формулы (8) следует, что напряжение
· Uобщ =  (14)
(14)
·
· а напряжение
· 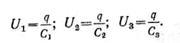
· Подставив эти выражения в формулу (14), получим:
·
·
· 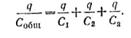
· Разделим левую и правую части этого равенства на величину q и после сокращения найдем:
· 
·
· Пример. Три конденсатора С1=2 мкф, С2=4 мкф и С3=8 мкф соединены последовательно. Определить их общую емкость.
· Решение.
· 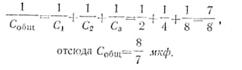
· Если последовательно соединены конденсаторы, имеющие одинаковую емкость, то их общую емкость можно вычислить по формуле
· 
·
· Пример. Четыре конденсатора емкостью 1000 пф каждый соединены последовательно. Определить их общую емкость. Решение.
· 
· 
·
· Если последовательно соединены два конденсатора различной емкости, то их общую емкость можно найти по формуле
·
· 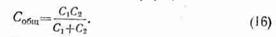
· Пример.
· Два конденсатора С1=200 пф и С2=300 пф соединены последовательно. Вычислить их общую емкость.
· Решение
· 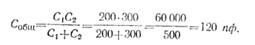
· Как видно из приведенных примеров, общая емкость конденсаторов, соединенных последовательно, всегда меньше наименьшей емкости, входящей в соединение.
· Конденсаторы выбирают по емкости и рабочему напряжению которое подается на его пластины при включении в схему. При напряжении, превышающем допустимое, происходит пробой диэлектрика в конденсаторе. Это напряжение называется пробивным. Пробой диэлектрика сопровождается электрическим разрядом — искрой с характерным треском. Конденсатор с пробитым диэлектриком не пригоден для применения.
· Каждый диэлектрик обладает определенной электрической прочностью, т. е. способностью противостоять пробою. Электрическая прочность (табл. 2) измеряется обычно в 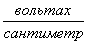 (в/см) и определяется по формуле
(в/см) и определяется по формуле
· 
·
· где U — напряжение, в,
· d — толщина диэлектрика, см.
·
· § 12. ПОНЯТИЕ ОБ ЭЛЕКТРОИСКРОВОМ СПОСОБЕ ОБРАБОТКИ МЕТАЛЛОВ
·
· Электрические разряды используют для обработки металлов. Советские изобретатели Б. Р. Лазаренко и Н. И. Лазаренко разработали новый электрический способ обработки металлов, который
· 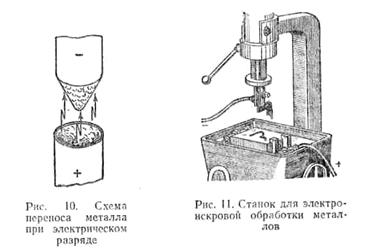
· назван электроискровым. Этот способ основан на том, что при электрическом разряде вместе с искрой с положительного электрода переносятся частицы металла и поэтому на нем образуется впадина, а на отрицательном электроде — выступ (рис. 10).
· Поверхностное разрушение электродов под действием электрического разряда называется электрической эрозией.
· При электроискровой обработке металлов (рис. 11) деталь помещают в ванну с водой, маслом или керосином и присоединяют к ней положительный полюс источника электрической энергий (анод).
· В качестве «инструмента» используют медно-графитовую пластину, имеющую форму того отверстия, которое хотят сделать в обрабатываемой детали. К инструменту подводят отрицательный полюс источника электрической энергии (катод).
· Инструмент (катод) приближают к обрабатываемой детали (к аноду), не касаясь ее, до расстояния, при котором начинается пробой— искрообразование. Частицы металла с большой скоростью вырываются из детали (анода) и, направляясь к катоду, попадают в жидкость. Это обеспечивает сохранение формы инструмента. По мере продвижения в массу металла инструмент автоматически опускается, в результате этого между ним и деталью сохраняется нужное для поддержания разряда расстояние.
· Через несколько минут после начала обработки изделия в металле большой твердости получается отверстие необходимой формы и размера.
· Электроискровым способом можно делать сквозные и глухие отверстия различной формы, изготовлять различные штампы, пресс-формы, шлифовать поверхности, затачивать и доводить твердосплавные резцы, разрезать металлы различной твердости, наносить покрытия на металлические поверхности, нарезать резьбу и выполнять другие всевозможные виды обработки металлов.
· Контрольные вопросы
· 1. Каким электрическим зарядом обладают электроны?
· 2. От каких величин зависит сила взаимодействия электрических зарядов?
· 3. Что называется электрическим полем?
· 4. Каким электрическим зарядом обладает тело, атомы которого имеют недостаток или избыток электронов?
· 5. Что называется электрическим потенциалом?
· 6. Что называется разностью потенциалов?
· 7. Что называется напряженностью электрического поля?
· 8. От каких величин зависит емкость плоского конденсатора?
· 9. Назовите единицы измерения электрической емкости и их соотношение.
· 10. При каком соединении конденсаторов общая емкость уменьшается?
· 11. Как вычислить емкость двух конденсаторов, соединенных последовательно, имеющих разную емкость?
· ГЛАВА II
· ПОСТОЯННЫЙ ТОК
·
· § 13. ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ПОСТОЯННОГО ТОКА
· Простейшая электрическая цепь (рис. 12) содержит источник электрической энергии Г, приемник энергии П и два линейных провода Л1 и Л2, соединяющих источник с приемником энергии. Линейные провода присоединяются к источнику электрической энергии при помощи двух зажимов, называе  мых положительным ( + ) и отрицательным (—) полюсами.
мых положительным ( + ) и отрицательным (—) полюсами.
· Источник электрической энергии преобразует механическую, химическую, тепловую или другого вида энергию в энергию электрическую. В приемнике происходит преобразование электрической энергии в энергию другого вида — механическую, тепловую, химическую, световую и др.
· Источниками электрической энергии служат генераторы (электрические

|
·
машины, приводимые в движение какими-либо механическими двигателями), аккумуляторы и гальванические элементы, условное обозначение которых показано на рис. 13. В качестве приемников электрической энергии применяют осветительные лампы, электрические двигатели, электронагревательные приборы и пр.
· Как гальванические элементы, так и аккумуляторы соединяют между собой для составления в первом случае батареи гальванических элементов, а во втором — батареи аккумуляторов. Источник электрической энергии с присоединенными к нему линейными проводами и приемником энергии образуют замкнутую электрическую цепь, по которой происходит непрерывное движение электричества, называемое электрическим током.
· Постоянный ток в металлических проводниках представляет собой установившееся поступательное движение свободных электронов в замкнутой цепи.
· Сила тока, протекающего в двух проводниках, отстоящих друг от друга на определенном расстоянии, вызывает механические силы, действующие на эти проводники. Единицей измерения силы тока является ампер (а). В Международной системе единиц (СИ) ампер—сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого круглого сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2 10-7 ньютона (н) на каждый метр длины.
· Единицей силы в Международной системе единиц является ньютон (н); н= 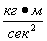 ,
,
· где кг – килограмм массы,
· м – метр,
· сек –секунда.
· Электрический ток определяет количество электричества, протекающего через поперечное сечение проводника в единицу времени. Если в проводнике протекает ток силой 1 а, то через поперечное сече-ние этого проводника в течение 1 сек протекает 1 к электричества.
· При силе тока в проводнике I за время t через поперечное сечение этого проводника протекает количество электричества, равное
· Q=It
· Откуда
· I= 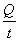
· I
· Эта зависимость справедлива для случая, когда в течение времени t сила тока остается неизменной.
· Таким образом, если через поперечное сечение проводника протекает 40 к электричества за 5 сек, то сила тока в цепи
· 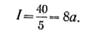
· Линейные провода и приемник энергии составляют внешнюю цепь, в которой ток протекает под действием разности потенциалов на зажимах источника энергии и направлен от точки более высокого потенциала (положительного зажима) к точке более низкого потенциала (отрицательного зажима)
· § 14. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
·
· Как было указано выше, в замкнутой цепи электрический ток протекает под действием электродвижущей силы (э. д. с.) источника энергии.
· Электродвижущая сила возникает в источнике тока и при отсутствии тока в цепи, т. е. когда цепь разомкнута. При холостом ходе, т. е. при отсутствии тока в цепи, э. д. с. равна разности потенциалов на зажимах источника энергии. Так же как и разность потенциалов э. д. с. измеряется в вольтах (в).
· Как при замкнутой, так и при разомкнутой электрической цепи э. д. с. непрерывно поддерживает разность потенциалов на зажимах источника энергии. Для непрерывного протекания тока в замкнутой цепи необходимо движение зарядов внутри источника тока в направлении, обратном действию сил поля.
· Такое перемещение зарядов происходит за счет энергии, вырабатываемой источником тока. Поэтому э. д. с. численно равна энергии, сообщаемой источником тока единичному положительному заряду. Если количеству электричества Q кулонов источник тока сообщает энергию А дж, то э. д. с. источника энергии
· 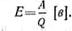
·
· Так как А = Рt и Q=It (где Р — мощность, развиваемая источником тока, вт, I — сила тока, а, t — время, сек), то
· 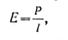
· т. е. электродвижущей силой может быть названо отношение мощности, развиваемой источником тока, к силе тока.
· В наличии э. д. с. можно убедиться путем присоединения к полюсам источника энергии (вместо линейных проводов) прибора, называемого вольтметром. Стрелка вольтметра при этом отклонится на некоторый угол. Отклонение будет тем больше, чем больше э. д. с. источника энергии. Однако вольтметр покажет не величину э. д. с, а, как мы увидим ниже, напряжение на зажимах источника тока, которое так же как и э. д. с. измеряется в вольтах.
· Высокие напряжения и э. д. с. выражены в киловольтах (кв); 1 кв=1000 в.
· Малые величины напряжений и э. д. с. выражают в милливольтах (мв); 1 мв = 0,001 в
· § 15. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ
· Направленному движению электрических зарядов в любом проводнике препятствуют его молекулы и атомы. Поэтому как внешняя цепь, так и сам источник энергии оказывают препятствие прохождению тока. Величина, характеризующая противодействие электрической цепи прохождению электрического тока, называется электрическим сопротивлением (или, короче, сопротивлением).
· Источник электрической энергии, включенный в замкнутую электрическую цепь, расходует энергию на преодоление сопротивления внешней и внутренней цепей.
· Электрическое сопротивление обозначается буквой r и на схемах изображается так. как показано на рис. 14, а
· 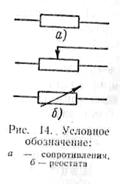 Единицей измерения сопротивления является ом. Омом называется электрическое сопротивление такого линейного проводника, в котором при неизменяющейся разности потенциалов в 1 в протекает ток силой в 1 а, т. е.
Единицей измерения сопротивления является ом. Омом называется электрическое сопротивление такого линейного проводника, в котором при неизменяющейся разности потенциалов в 1 в протекает ток силой в 1 а, т. е.
· 1 ом = 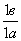
· При измерении больших сопротивлений используют единицы в тысячу и в миллион раз больше ома. Они называются килоомом (ком) и мегоомом (Мом); 1 ком =1000 ом; 1 Мом = 1 000 000 ом.
· В различных веществах содержится различное количество электронов, а атомы, между которыми эти электроны движутся, имеют различное расположение. Поэтому сопротивление проводников электрическому току зависит от материала, из которого они изготовлены, от длины и площади поперечного сечения проводника. Если сравнить два проводника, изготовленных из одного и того же материала, то более длинный проводник имеет большее сопротивление при равных площадях поперечных сечений, а проводник с большим поперечным сечением имеет меньшее сопро-тивление при равных длинах.
· Для оценки электрических свойств материала проводника служит удельное сопротивление — это сопротивление проводника длиной в 1 м и площадью поперечного сечения в 1 мм2. Удельное сопротивление обозначается буквой .
· Если проводник, изготовленный из материала с удельным сопротивлением , имеет длину l метров и площадь поперечного сечения q квадратных миллиметров, то сопротивление всего проводника
· 
· Эта формула указывает на то, что сопротивление проводника прямо пропорционально удельному сопротивлению материала, из которого он изготовлен, а также его длине и обратно пропорционально площади поперечного сечения.
· Сопротивление проводников зависит от температуры, причем сопротивление металлических проводников с повышением температуры увеличивается. Для каждого металла существует определенный, так называемый температурный, коэффициент сопротивления, который выражает прирост сопротивления проводника при измнении температуры на 10 С отнесенный к 1 ом начального сопротивления.
· Таким образом, температурный коэффициент сопротивления
· 
·
· где r1 - сопротивление проводника при температуре T1,
· r2 - сопротивление того же проводника при температуре T2,
· Поясним выражение для температурного коэффициента сопротивления на примере. Положим, что медный линейный провод при температуре T1= 15° С имеет сопротивление r1 = 75 ом, а при температуре T2= 75°С r2=93 ом. Следовательно, прирост сопротивления при изменении температуры на 75—15 = 60° С составляет 93—75 = = 18 ом. Таким образом, прирост сопротивления, соответствующий изменению температуры на 1°С, равен 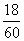 =0,3.
=0,3.
· Для определения температурного коэффициента сопротивлений нужно этот прирост сопротивления отнести к 1 ом начального сопротивления, т. е. разделить на 75:
·
· 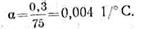
· Соотношение между сопротивлениями r1 и r2:
·
· 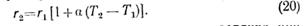
·
· Следует иметь в виду, что это соотношение справедливо при не очень высоких температурах, а для измерения сопротивлений при температурах выше 100—150° С оно не может быть использовано.
· Регулируемые сопротивления называются реостатами. Реостаты изготовляют из проволоки с большим удельным сопротивлением, например из нихрома. Сопротивление реостатов может изменяться равномерно или ступенями. Применяют также жидкостные реостаты, представляющие собой металлический сосуд, наполненный каким-либо раствором, проводящим электрический ток, например раствором соды в воде. На схемах реостаты условно обозначают так, как показано на рис. 14, б.
· Способность проводника пропускать электрический ток характеризуется проводимостью, которая представляет собой величину, обратную сопротивлению, и обозначается буквой g. Единицей измерения проводимости является 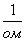 (сименс).
(сименс).
· 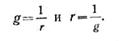
· Величина обратная удельному сопротивлению материала проводника, называется удельной проводимостью и обозначается буквой .
· Таким образом, между удельным сопротивлением и удельной проводимостью вещества имеют место следующие соотношения:
· 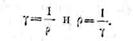
· Пример 1. Определить длину медной проволоки диаметром 1 мм, имеющей сопротивление 15 ом, зная, что удельное сопротивление меди 0,0175 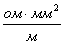 .
.
· Решение: поперечное сечение провода равно:
· 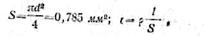
· откуда
·
· 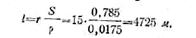
·
· Пример 2. Определить поперечное сечение нихромовой проволоки = 1 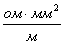 , имеющей при длине 40 м сопротивление 50 ом.
, имеющей при длине 40 м сопротивление 50 ом.
· Решение:
· 
· откуда
·
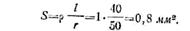
|
·
·
· Пример 3. Обмотка трансформатора, изготовленная из медного провода, в нерабочем состоянии при 15° С имела сопротивление r1=2 ом. При работе сопротивление ее стало равным r2=2,48 ом. Определить температуру обмотки в рабочем состоянии, зная, что температурный коэффициент меди 0,004.
· Решение.
·
· 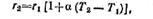
·
· откуда
· 
·
· § 16. ЗАКОН ОМА
· Соотношение между э. д. с, сопротивлением и силой тока в замкнутой цепи выражается законом Ома, который может быть сформулирован так: сила тока в замкнутой цепи прямо пропорциональна электродвижущей силе и обратно пропорциональна сопротивлению всей цепи.
· Ток в цепи протекает под действием э. д. с; чем больше э. д. с. источника энергии, тем больше и сила тока в замкнутой цепи. Сопротивление цепи препятствует прохождению тока, следовательно, чем больше сопротивление цепи, тем меньше сила тока.
· Закон Ома можно выразить следующей формулой:
·
· 
· или
· 
· где r — сопротивление внешней части цепи,
· r0 — сопротивление внутренней части цепи.
· В этих формулах сила тока выражена в амперах, э. д. с. — в вольтах, сопротивление — в омах.
· Для выражения малых токов вместо ампера применяют единицу, в тысячу раз меньшую ампера, называемую миллиампером (ма); 1 а — 1000 ма.
· Сопротивление всей цепи:
· 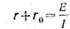
Дата добавления: 2021-04-21; просмотров: 441;











