Получение и особенности сверхзвуковых потоков

Впервые сверхзвуковое течение газа было получено в конце 19 века шведским инженером Лавалем в трубе переменного сечения, названной впоследствии соплом Лаваля.

Сопло Лаваля представляет собой насадок, состо-

ящий из короткой сужающейся части и следующей за ней более длинной расширяющейся части.

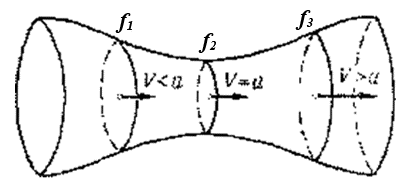
Рис. 3.2. Сопло Лаваля

Сопло Лаваля может работать в расчётном и нерасчётном режимах.

Если в самом узком сечении сопла, называемом критическим, местная скорость потока становится равной местной скорости звука, то в расширяющейся части сопла поток становится сверхзвуковым. Такой режим работы сопла называется расчётным.

Если через сопло Лаваля протекает газ со скоростью, меньшей скорости звука, то во входной части сопла скорость нарастает, в критическом сечении достигает максимума и в выходной части убывает.

Сверхзвуковое течение газа имеет следующие особенности:

1) для увеличения скорости потока поперечное сечение необходимо увеличивать;

2) волны слабых возмущений не могут распространяться впереди тела, летящего со сверхзвуковой скоростью, а распространяются за ним в виде конуса, называемого конусом Маха;

3) при торможении сверхзвукового потока всегда возникают скачки уплотнения.

Первая особенность

Первая особенность объясняется, тем, что удельный расход газа 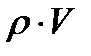с увеличением скорости в дозвуковом диапазоне скоростей увеличивается, а в сверхзвуковом – уменьшается.

Как следует из уравнения неразрывности, в случае сжигаемого газа площадь поперечного сечения струйки обратно пропорциональна произведению плотности газа на его скорость.

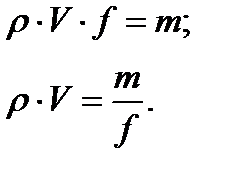
Рис. 3.3. Секундный массовый расход m

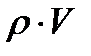Произведение называется удельным расходом газа, так как оно равно массе газа, протекающей за 1 сек через единицу площади поперечного сечения струйки. (рис. 3.3)

Расмотрим, как изменяется удельный расход газа с изменением скорости вдоль струйки.

Рис. 3.4. Изменение плотности с ростом скорости

Из термодинамики известна зависимость плотности воздуха от скорости его течения (рис. 3.4).

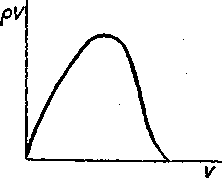
Рис. 3.5. Зависимость удельного расхода газа от скорости

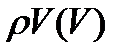Если, пользуясь этим графиком, построить зависимость , то она будет иметь вид, представленный на рис. 3.5.

Такое течение графика объясняется тем, что на дозвуковых скоростях с ростом скорости плотность уменьшается медленнее, чем увеличивается скорость,
и произведение 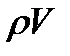возрастает, а на сверхзвуковых скоростях происходит резкое падение плотности при увеличении скорости и удельный расход 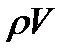уменьшается.

Максимуму удельного расхода соответствует минимальное сечение струи. Эта точка соответствует скорости V, равной скорости звука .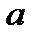

Следовательно, на дозвуковых скоростях для увеличения скорости поперечное сечение струйки необходимо уменьшать, а на сверхзвуковых – увеличивать.

Вторая особенность

Для объяснения второй особенности рассмотрим картину распространения звуковых волн в сверхзвуковом потоке. От источника возмущений возмущения распространяются во все стороны со скоростью звука а в виде сферических волн уплотнения или разрежения. В неподвижной среде границей возмущенной
зоны является расширяющаяся сферическая поверхность с центром в источнике возмущений.

При равномерном течении среды сферические волны. Возникающие в источнике возмущений, сносятся потоком в направлении скорости течения.

За время t радиус сферической волны, исходящей из возмущающей точки, станет равным 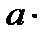t, а центр волны будет снесен потоком на расстояние V t относительно той же точки. Волны, возникающие позднее,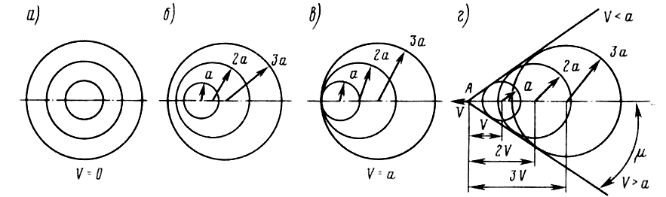
имеют меньший радиус и находятся ближе к центру.

Рис. 3.6. Распределение звуковых волн

Поверхность, огибающая сферические волны, образует конус возмущений с вершиной в источнике возмущений. Синус угла при вершине такого конуса может быть представлен в виде

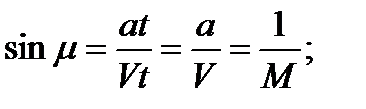
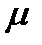— угол слабых возмущений (это угол между линией слабых возмущений и линией потока).

Конус слабых возмущений называется конусом Маха, так как угол 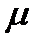зависит от числа М.

Коническая поверхность с углом раствора 2 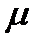вляется границей, в пределах которой распространяются малые возмущения и за пределы которой они не выходят.

Чем больше число М полета, тем меньше угол раствора конуса, тем меньше возмущенная зона. При уменьшении числа М угол 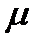увеличивается, тем самым увеличивается возмущенная зона.

Когда газовый поток движется со скоростью, равной скорости звука.

(V= 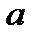; M=1), угол слабых возмущений 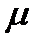=90 .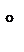
В этом случае границей возмущения является плоскость, нормальная к направлению скорости (рис. 3.6, в).

Третья особенность

При торможении сверхзвукового потока в нем появляются скачки уплотнения, что объясняется результатом наложения слабых возмущений. Тело, обтекаемое потоком воздуха, является совокупностью множества точечных источников возмущений. В сверхзвуковом потоке слабые возмущения точечных источников – конусы возмущений – суммируются, создавая более сильное возмущение среды. Скачок уплотнения представляет собой границу возмущений, вызванных телом.

Скачком уплотнения называется тонкий плотно сжатый слой воздуха, образующийся при торможении сверхзвукового потока.

Толщина скачка примерно равна удвоенной длине свободного пробега молекул, т.е. очень мала.

При переходе через скачок уплотнения сверхзвуковой поток теряет часть своей кинетической энергии в результате преобразования ее в энергию давления и тепловую энергию. Поэтому одновременно с резким уменьшением скорости V в скачке происходит столь же резкое повышение давления р, плотности 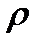и температуры Т.

Скачки уплотнения бывают:

· прямые

· косые

· криволинейные

Прямым называется скачок уплотнения, поверхность которого перпендикулярна набегающему потоку. При переходе через такой скачок поток всегда
становится дозвуковым (рис. 3.7,а).

Косым называется скачок уплотнения, поверхность которого расположена под углом к набегающему потоку (рис. 3.7, б).

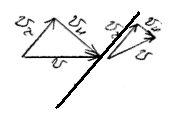
При переходе через косой скачок поток тормозится меньше, чем на прямом, так как уменьшается только нормальная составляющая скорости потока, а тангенциальная составляющая V сохраняет своё значение. Это вызывает изменение направления потока за скачком. За косым скачком скорость полёта может оставаться сверхзвуковой.

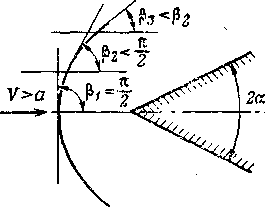При обтекании конуса с большим углом раствора или тел с закруглённой носовой частью поверхность скачка отходит от тела и приобретает криволинейную форму. Такой скачок уплотнения называется криволинейным.

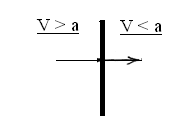
а

в

б

Рис. 3.7. Скачки уплотнения: а) прямой; б) косой; в) криволинейный

Криволинейный скачок можно рассматривать как серию косых скачков с разными углами наклона. В носовой части тела такой скачок имеет элемент прямого скачка, а каждый последующий элемент скачка имеет все больший угол наклона.

Рис. 3.8. Скачки уплотнения

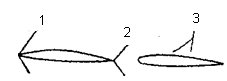По расположению скачка относительно тела бывают скачки уплотнения головные (1), хвостовые (2), местные (3).