Оптимизация размеров активного элемента
При аналитическом расчете выходной мощности ОКГ наиболее часто используют подход Ригрода, который позволяет с достаточной точностью проанализировать энергетику ОКГ. При таком методе описания ОКГ используются следующие основные допущения:
1.Линия усиления рабочего вещества ОКГ считается однородно уширенной.
2.Превышение уширения над порогом генерации невелико
Для описания параметров АЭ и элементов резонатора используются следующие величины:
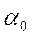 - ненасыщенный показатель усиления ;
- ненасыщенный показатель усиления ;
IS – плотность потока мощности насыщения;
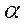 - распределенные потери в рабочем веществе;
- распределенные потери в рабочем веществе;
LАЭ – длина активного элемента;
S0 – площадь поперечного сечения активного вещества;
Т0 – коэффициент пропускания выходного зеркала оптического резонатора;
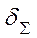 - суммарные потери на зеркалах.
- суммарные потери на зеркалах.
Мощность на выходе ОКГ в этих обозначениях определится соотношением:
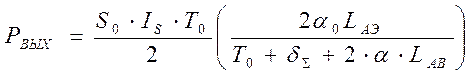 . (4.19)
. (4.19)
Таким образом, задачей проектирования является нахождение величин 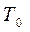 ,
, 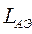 ,
, 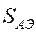 . Очевидно, что задача проектирования является типичной задачей многофакторной оптимизации, так как требуемое значение выходной мощности может быть получено, при различных наборах параметров резонатора
. Очевидно, что задача проектирования является типичной задачей многофакторной оптимизации, так как требуемое значение выходной мощности может быть получено, при различных наборах параметров резонатора 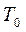 ,
, 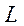 ,
, 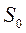 . Поскольку длина активной среды лазера
. Поскольку длина активной среды лазера 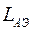 определяет габаритные размеры ОКГ, а сечение
определяет габаритные размеры ОКГ, а сечение 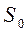 связано с процессом создания инверсной заселенности и определяет пространственные характеристики излучения ОКГ, то оптимизацию целесообразно начинать с нахождения
связано с процессом создания инверсной заселенности и определяет пространственные характеристики излучения ОКГ, то оптимизацию целесообразно начинать с нахождения
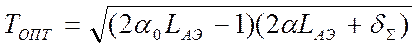 . (4.20)
. (4.20)
Из (4.20) видно, что  не зависит в явном виде от
не зависит в явном виде от  . Однако, в случае использования открытого устойчивого резонатора эта величина будет сильно зависеть от величины потерь
. Однако, в случае использования открытого устойчивого резонатора эта величина будет сильно зависеть от величины потерь  .
.
Подставляя (4.20) в (4.19) получаем выражение для выходной мощности ОКГ при оптимальной прозрачности выходного зеркала:
 . (4.21)
. (4.21)
Для оценки эффективности преобразования энергии целесообразно ввести понятие КПД резонатора как отношение выходной мощности ОКГ к полному запасу мощности в активной среде:
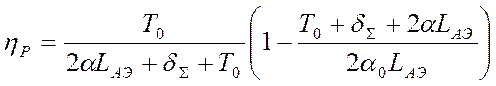 . (4.22)
. (4.22)
С учетом (4.20):
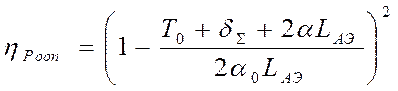 . (4.23)
. (4.23)
Из (4.19) видно, что условие самовозбуждения ОКГ ( 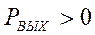 ) имеет вид:
) имеет вид:
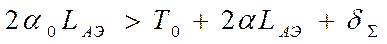 . (4.24)
. (4.24)
Соотношение (4.24) определяет минимальное значение длины активной среды лазера:
При 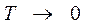 ,
, 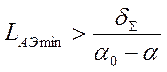 , (4.25)
, (4.25)
Рассмотрим ограничения на длину активной среды ОКГ сверху. Из (4.23) очевидно, что при выполнении условия
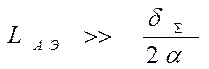 . (4.26)
. (4.26)
КПД резонатора не зависит от длины АЭ, так как потери в ней будут превышать потери на зеркалах резонатора. Подобный режим работы возможен лишь в тех случаях, когда не предъявляются жесткие требования к пространственным характеристикам излучения ОКГ. Это связано с тем, что при выполнении неравенства (4.26) основную роль в формировании пространственных характеристик излучения ОКГ играют неоднородности активного вещества, а не свойства резонатора ОКГ.
Помимо неравенства (4.26) ограничение на величину 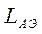 сверху накладывает то обстоятельство, что
сверху накладывает то обстоятельство, что 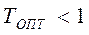 . Учитывая это, из (4.21), полагая, что:
. Учитывая это, из (4.21), полагая, что:
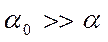 ;
; 
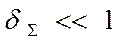 . (4.27)
. (4.27)
получаем
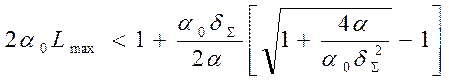 . (4.28)
. (4.28)
В реальных условиях, учитывая допущения (4.27) неравенство (4.28) должно выполняться с запасом. Невыполнение условия (4.28) приводит к переходу ОКГ в режим “сверхизлучения”, когда формирование пространственных характеристик излучения не связано со свойствами резонатора. Таким образом, неравенство (4.28) определяет условия выбора длины активного вещества ОКГ и соответствующей длины резонатора. По соотношению (4.21) рассчитывается коэффициент пропускания выходного зеркала резонатора.
На практике протяженность активной среды может быть определена по методу линейной аппроксимации, как
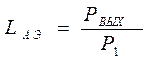 , (4.29)
, (4.29)
где 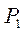 - удельная мощность излучения, для данного диаметра стержня. Диаметр активного элемента также можно рассчитать по методу линейной аппроксимации, с округлением до ближайшего стандартного размера.
- удельная мощность излучения, для данного диаметра стержня. Диаметр активного элемента также можно рассчитать по методу линейной аппроксимации, с округлением до ближайшего стандартного размера.
В тех случаях, когда ОКГ не предъвлются требования работы на одной моде, расчет поперечных размеров активного элемента следует производить из условия оптимизации Рвых (выходной мощности генератора). В общем случае мощность излучения должна расти с увеличением поперечного сечения. Однако на практике существует ряд факторов, которые препятствуют этому. Например, в ТТ ОКГ с оптической накачкой или в ОКГ на углекислом газе накачка может обеспечить надпороговую инверсиютолько в некоторой эффективной зоне поперечного сечения. Последняя не увеличивается с ростом всего сечения. В ряде типов газоразрядных ОКГ увеличение сечения ведет к резкому уменьшению 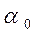 . Поэтому в каждом конкретном случае вопрос о рациональном выборе поперечного размера активного элемента должен решаться особо. Сечение АЭ обычно представляет собой круг, и задача таким образом сводится к рациональному выбору диаметра активного элемента d. В ТТЛ излучение накачки проникает в толщу активного элемента, как правило, через боковую цилиндрическую поверхность. Так как при прохождении через среду излучение частично поглощается, то в центральных участках объемная плотность “накачки” меньше, чем в поверхностных. При экспоненциальном характере затухания плотность энергии в центре сечения определится:
. Поэтому в каждом конкретном случае вопрос о рациональном выборе поперечного размера активного элемента должен решаться особо. Сечение АЭ обычно представляет собой круг, и задача таким образом сводится к рациональному выбору диаметра активного элемента d. В ТТЛ излучение накачки проникает в толщу активного элемента, как правило, через боковую цилиндрическую поверхность. Так как при прохождении через среду излучение частично поглощается, то в центральных участках объемная плотность “накачки” меньше, чем в поверхностных. При экспоненциальном характере затухания плотность энергии в центре сечения определится:
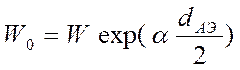 , (4.30)
, (4.30)
где W- плотность энергии “накачки” на поверхности активного элемента;
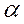 - показатель поглощения излучения “накачки”.
- показатель поглощения излучения “накачки”.
При увеличении диаметра плотность энергии в центре сечения может стать меньше пороговой Wп. Отношение плотностей энергии “накачки” приблизительно можно заменить отношением показателей усиления
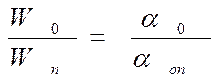 , (4.31)
, (4.31)
где 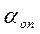 - пороговое значение показателя усиления.
- пороговое значение показателя усиления.
Таким образом, оптимальный диаметр активного элемента может быть найден из (4.30) с учетом (4.31):
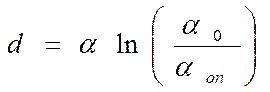 . (4.32)
. (4.32)
Пороговое значение показателя усиления определяется соотношением:
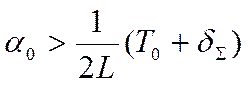 . (4.33)
. (4.33)
Величины Xн для основных материалов активных элементов приведены в таблице
Таблица 4.4. Коэффициенты затухания.
| Параметр | Материал | ||
| Рубин | YAG:Nd | Cm:Nd | |
| Xн, см-1 | -1,4 | -1,2 | -1,0 |
Следует иметь в виду, что d должен быть меньше диаметров каустики высшей генерируемой моды в соответствующих сечениях, которые получаются из расчета оптического резонатора. В противном случае выходная мощность будет уменьшаться из-за увеличения дифракционных потерь.
Дата добавления: 2016-12-16; просмотров: 2096;











