ЛЕКЦИЯ 3. 3.1. Момент силы относительно точки.
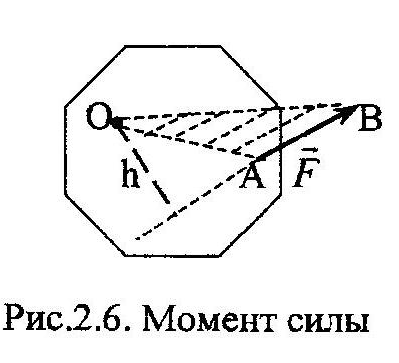
Моментом силы количественно характеризуется эффект ее воздействия на тело, при котором тело получает угловое перемещение (рис.2.6.).
Моментом силы относительно центра, m0(F), называется величина, равная произведению модуля силы, F, на длину ее плеча, h, т.е.
 где h – плечо силы, равное кратчайшему расстоянию от центра О до линии действия силы. Величина момента считается положительной, если сам вектор силы, F,
где h – плечо силы, равное кратчайшему расстоянию от центра О до линии действия силы. Величина момента считается положительной, если сам вектор силы, F,
|
|
вращается относительно центра против часовой стрелки (как показано на рис. 2.6) и отрицательной, если это вращение происходит по часовой стрелке.
Свойства момента силы относительно центра:
1. Величина момента силы не изменится, если ее точку приложения перенести по
Линии действия.
Действительно, при переносе силы не меняется ни ее модуль, ни плечо. Поэтому произведение в правой части (2.11) не изменится.
2. Момент силы равен нулю, когда ее линия действия пересекает данный центр.
3. Момент силы численно равен удвоенной площади треугольника OAB, построенного
на силе и центре (рис. 2.6), т.е.: m0(F)=2SΔOAB.
Действительно,
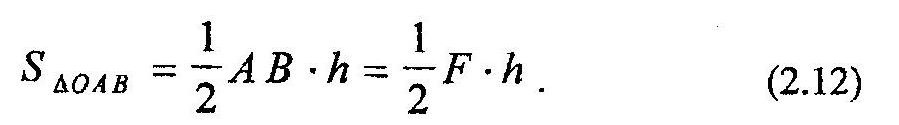
Сравнивая правую часть полученного выражения (2.12) с формулой момента силы (2.11), заключаем, что площадь треугольника равна половине величины момента силы, что и означает третье свойство момента силы.
Теорема Вариньона
Дата добавления: 2016-12-16; просмотров: 1927;











