Разделение и фракционирование ключей. Пороговая криптография

Прежде мы рассматривали различные способы хранения и управления секретными ключами, которые управляют биткоинами, но мы всегда держали ключ в одном и том же месте - сейфе, программе или на бумаге. Но у всех них есть одно слабое место: если что-то случится с местом хранения, будут проблемы. Можно делать резервные копии, но хотя это ослабляет проблему доступности, это увеличивает вероятность кражи.

Одно всегда приносится в жертву другому. Но можно ли взять часть данных и хранить его так, чтобы доступность и безопасность увеличивались одновременно? Как ни удивительно, ответ на это - да, и снова на помощь нам приходит криптография, а вернее, тот её метод, который называется тайным фракционированием. Идея состоит вот в чём: мы разделяем наш ключ на N фракций, причём таким образом, чтобы при любом К этих частей можно было восстановить весь ключ, но если у нас в распоряжении меньше, чем К частей, то об исходном ключе ничего узнать будет невозможно.

С учётом этого требования нельзя просто взять и поделить ключ на несколько частей, поскольку каждый из них будет нести часть информации о целом. Тут нужно что-то более хитрое. И поскольку мы не делим секрет, мы называем эти части фракциями, а не частями. Скажем, N=2 и K=2. Это значит, что мы создаём две фракции на основе секрета, и нам нужны они обе, чтобы восстановить его весь. Пусть секрет обозначается как S, и является большим, например, 128-битным числом.

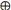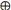Мы можем сгенерировать случайное 128-битное число R и составить его из двух фракций по операции S R ( означает побитное исключённое ИЛИ). Естественно, мы зашифровали S и храним как ключ R, так и шифротекст S 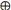R в разных местах. Ни ключ, ни шифротекст сами по себе ничего не говорят о секрете. Но совместив их, мы просто делаем операцию исключённого ИЛИ, чтобы восстановить секрет. Этот трюк работает, пока N и К одинаковы - нужно просто сгенерировать N-1 разных случайных чисел для первых N-1 фракций, а последняя будет секретом после исключённого ИЛИ с остальными N-1 фракциями. Но если N>K, система уже не работает, и нам нужно привлекать математику.

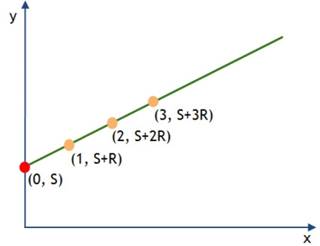
Рис. 4.3: Геометрическая иллюстрация секретного фракционирования 2-ro-N. S - секрет, зашифрованный в виде большого целого числа. Зелёная линия имеет случайный уклон. Любые две оранжевые точки (а именно, их ординаты S+R, S+2R, ...) соответствуют фракциям. Любых двух оранжевых точек достаточно для получения красной точки, т. о., и секрета. Все операции выполняются по модулю большого изначального числа

Посмотрим на рисунок 4.3. Здесь мы сначала сгенерировали точку с координатами (0, S) на оси ординат, а затем провели линию случайного наклона по этой точке. Затем мы сгенерировали группу точек на этой линии - столько, сколько нам угодно. В данном случае фракционирование секрета S, N - число точек, которые мы сгенерировали, а К=2. Почему это работает? Как минимум потому, что через любые две точки можно провести прямую и посмотреть, где она пересекает ось ординат - что даст нам S.

С другой стороны, имея только одну точку, вы ничего с её помощью не узнаете об S, поскольку наклон прямой был выбран случайно, и любая из них будет пересекать ось ординат в разных местах и имеет одну и ту же вероятность быть нужной. Есть, правда, одна тонкость: чтобы вся эта математика работала, нужно взять арифметический модуль от неделимого Р Оно не должно быть секретным, оно просто должно быть огромным. А секрет должен находиться в интервале от 0 до Р-1 включительно.

Так что, говоря, что мы генерируем точки на прямой, мы имеем в виду, что генерируем случайное R на интервале от 0 до Р-1, и получаем следущие точки:
x=1, y=(S+R) mod P
x=2, y=(s+2R) mod P
x=3, y=(S+3R) mod P
и так далее. Секрет соответствует точке x=0, y=(S+0*R) mod P, которая просто x=0, y=S.

Здесь мы показали пример фракционирования секрета с К=2 и произвольным N. Это уже достаточно эффективно - скажем, если N=4, можно разделить секретный ключ на 4 фракции, поместить их в четыре разных устройства, и если кто-то похитит одно из них, то не узнает о ключе совершенно ничего. С другой стороны, если два из них, например, сгорят в пожаре, ключ можно будет восстановить из оставшихся двух. Таким образом, как мы и хотели, безопасность и доступность выросли одновременно.

Однако, можно всё сделать ещё лучше: можно осуществить фракционирование при любых К и N, если К не превышает N. Как? Посмотрим на рисунок. То, что мы воспользовались прямой, а не другой линией, неслучайно - в алгебраическом смысле она является полиномом первой степени. Это значит, что для восстановления её нам нужно не больше и не меньше, чем две точки. Если бы К было равно трём, нам понадобилась бы парабола, она же квадратичный полином или полином второй степени - для её восстановления нужно именно три точки. Из таблицы внизу можно понять, о чем вообще речь.

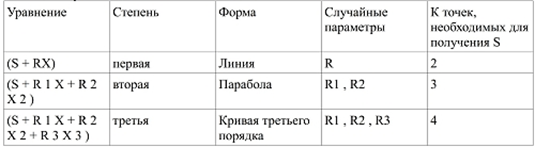
Таблица 4.1: Математика фракционирования. Представление секрета в форме серии точек на случайной полиномиальной кривой порядка К-1 позволяет восстановить секрет, только если доступно не менее К точек (фракций)

Есть формула, известная как интерполирование Лагранжа, которая позволяет восстановить полином степени К-1 на основании К точек кривой. Это алгебраический вариант и обобщение геометрически интуитивного рисования прямой через две точки по линейке. В итоге у нас есть способ хранить любой секрет в форме N фракций, что способно обезопасить его, даже если злодей узнает о K-1 из них, и в то же время, мы не потеряем к нему доступа, даже если утратим N-K из них.

К слову, ничто из этого не характерно для биткоина. Можно таким способом засекретить свои пароли хоть сейчас и раздать фракции друзьям или поместить их в разные устройства - однако с такими вещами, как пароли, в жизни так никто не поступает. Причина тому - обычное удобство. Ещё дело в том, что есть и другие механизмы безопасности для важных интернет-аккаунтов, например двухшаговое подтверждение с смс-верификацией. Однако в случае биткоина, если вы храните свои ключи на месте, у вас нет подобных вариантов.

Нельзя контролировать биткоин-адрес по смс. Ситуация отличается в случае онлайн-кошельков, которые мы будем рассматривать в следующем разделе, однако не слишком сильно - в данном случае проблема просто перемещается в другую область. В конечном итоге провайдер онлайн-кошелька тоже как-то должен избегать этого слабого места при хранении ключей.

Пороговая криптография. Но и здесь есть проблема с фракционированием: если возьмём ключ и расщепим его таким образом, а потом нам потребуется собрать его воедино, нам всё равно будет нужно свести вместе фракции и перерасчитать начальый секрет, чтобы ключом можно было поставить подпись. То, где мы сводим все фракции - это по сути та же единственная точка уязвимости, где наш злодей может попытаться украсть ключ. Криптография, однако, способна решить и эту проблему: если все фракции хранятся на разных устройствах, есть возможность создать подпись децентрализованно без реконструирования приватного ключа на едином устройстве.

Это называется "пороговой подписью". Наилучший вариант - кошелёк с двухшаговым подтверждением, соответствующий случаю N=2 и К=2. Положим, вы настроили свой кошелёк так, чтобы он разделил материалы ключа между телефоном и компьютером. Затем вы можете инициировать платёж с компьютера - это создаст частичную подпись и отправит её на телефон. С телефона вы узнаете реквизиты платежа - получателя, сумму и т.д. - и дадите подтверждение. Если всё хорошо, телефон завершит подпись своей фракцией приватного ключа и передаст транзакцию в блокчейн.

Если же у вас на компьютере вирус, пытающийся украсть биткоины, он может запустить транзакцию, отправляющую биткоины хакеру, но тогда вы получите сообщение на телефон о транзакции, которую не инициировали, и узнаете, что дело нечисто. Математические подробности пороговых подписей очень сложны и мы не будем их здесь обсуждать.

Мультисигнатурность. Есть и совершенно другой способ обойти злополучное слабое место - мультисигнатурность (то есть, требование нескольких подписей), о которой шла речь в лекции 3. Вместо того, чтобы брать и расщеплять один ключ, скрипт биткоина допускает непосредственное разделение контроля за адресом между несколькими ключами. эти ключи могут храниться в разных местах, и их подписи будут генерироваться независимо.

Конечно, завершённая и подписанная транзакция будет собираться на одном устройстве, но даже если злодей получит его в своё распоряжение, всё, что он сможет сделать - это помешать информации попасть в сеть. Он не сможет сотворить валидные подписи по другим транзакциям без владения остальными устройствами.

Для примера представим, что Эндрю, Арвинд, Эд, Джозеф и Стивен - авторы этой книги - совместно основали компанию, например, использовав для этого авторские отчисления за эту бесплатную книгу, и у нашей компании много биткоинов. Мы можем пользоваться мультисигом для защиты наших денег. Каждый из пятерых сгенерирует пару ключей и мы защитим своё холодное хранилище по схеме 3 из 5, что означает валидацию транзакции по подписям троих участников.

В итоге мы можем быть уверены в своей относительной безопасносии, если будем держать свои ключит по отдельности и пользоваться разными методами безопасности. Злодею придётся взломать сразу три отдельных ключа. А если один или даже двое из нас займутся беспределом, они не смогут украсть у компании деньги, так как для этого нужно не меньше трёх ключей.

В то же время, если один из нас потеряет ключ или попадёт под автобус, а мнемонический кошелёк будет утрачен, остальные всё же смогут получить назад свои коины и перевести их на новый адрес, где вновь обезопасят ключи. Иными словами, мультисиг помогает управлять большим количеством коинов на холодном хранении относительно безопасным образом, который требует сложных действий от нескольких людей.

Примечание. Пороговые подписи — это криптографическая техника для разделения целостного ключа на фракции и подписывания транзакций без реконструирования ключа. Мультисигнатурность — это особенность биткоин-скрипта, с помощью которой можно разделить контроль над адресом между несколькими независимыми ключами. Хотя они и различны, оба способа позволяют усилить безопасность и избежать слабых мест.