Надежность элементов конструкции технической системы по основным критериям

В сложных технических системах отказ даже одного элемента кон­струкции может привести к серьезным последствиям. Поэтому основ­ной задачей инженера-конструктора и специалиста по надежности яв­ляется оценка надежности элементов конструкции системы с учетом стоимостных факторов.

В основу расчетов надежности заложено то, что каждый элемент обладает определенной прочностью (или, например, жесткостью, из- ностойкостью, теплостойкостью, виброустойчивостью) по отношению к нагрузкам. Обычный способ проектирования, основанный на примене­нии коэффициентов безопасности и запаса прочности, не позволяют судить о вероятности отказа элемента.

Считается, что отказ элемента можно полностью исключить, исполь­зуя определенное достаточно высокое значение коэффициента безо­пасности. В действительности же при одном и том же коэффициенте безопасности вероятность отказа может колебаться в весьма широких пределах.

Использование коэффициентов безопасности оправдано только в случае наличия большого опыта проектирования и эксплуатации рас­считываемого элемента конструкции Однако необходимо учитывать, что конструктивные параметры часто являются случайными величи­нами, что полностью игнорируется при обычных методах проектиро­вания. Поэтому необходима методика проектирования с учетом веро­ятностного характера конструктивных параметров и нагрузок, воспри­нимаемых рассчитываемым элементом конструкции.

Оценка надежности по критерию прочности

В настоящее время накоплен значительный объем данных о рас­пределениях прочности и распределениях напряжений, воспринимае­мых элементами конструкций различных технических средств. В рас­четах основных деталей машин прочность определяют по соотноше­нию расчетного напряжения σ_а и предельного по критерию прочности напряжения детали σ_д, превышение которого вызывает отказ.

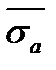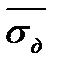Напряжения σ_а и σ_д рассматривают как независимые случайные величины, распределение которых характеризуется свойствами мате­риала деталей и условиями и режимами работы технических средств. В большинстве случаев по данным [1] напряжения σ_а и σ_д рассматри­вают распределенными по нормальному закону с числовыми характе­ристиками: средние значения и ; средние квадратические от­клонения S_a и S_д или коэффициенты вариаци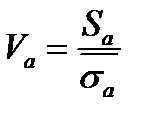и

и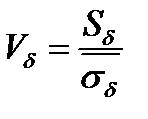

Вероятность безотказной работы по критерию прочности, назы­ваемой также вероятностью неразрушения, определяют как вероятность того, что расчетные напряжения σ_а не превышают пре­дельных σ_д, т.е. P( σ_а <σ_д )Числовое значение вероятности нераз­рушения определяют по таблицам нормального распределения (см. табл. 1) в зависимости от квантили

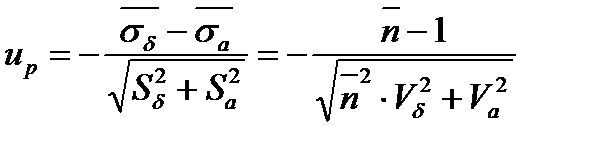
где 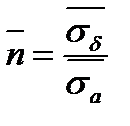- коэффициент запаса прочности по средним напряжениям.

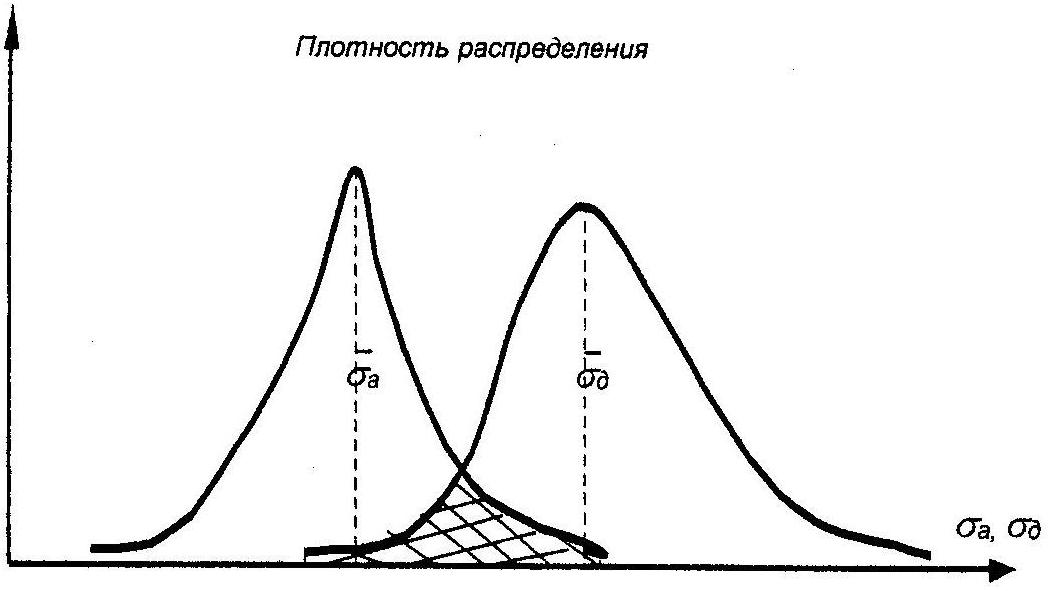
Рис. 38. Перекрытие распределения напряжений

Пример

Элемент металлоконструкции подвергается нагрузке, изменяю­щейся по закону нормального распределения с математическим ожи­дание напряжения 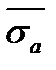=120 Мпа и средним квадратическим отклоне­нием S_a=30 Мпа. Вычислить вероятность безотказной работы детали, если ее прочность имеет нормальное

распределение с математическим ожиданием 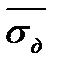= 180 Мпа и сред­ним квадратическим отклонением S_δ= 40 Мпа,

Решение

Определим квантиль по формуле

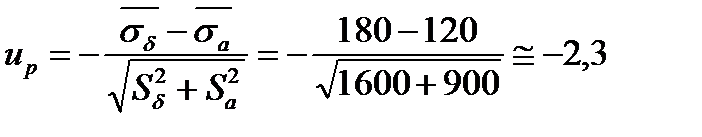
По таблице № 1 находим вероятность безотказной работы элемен­та металлоконструкции Р= 0,9893.

Экспериментальные исследования различных авторов показали, что прочностные свойства сплавов часто имеют логарифмически нор­мальное распределение. Распределение прочности сплавов на осно­ве железа часто характеризуют распределением Вейбулла. При ис­следовании влияния термической обработки, чистоты поверхностей и температуры на распределение усталостной прочности установлено, что эти факторы могут изменять функцию распределения. С другой стороны распределение действующих напряжений зависит от условий эксплуатации и режимов работы, и функции описания их могут быть различными. В этой ситуации, когда законы распределения прочности и действующих напряжений разные, вероятность безотказной работы по условию прочности в общем виде определяется выражением

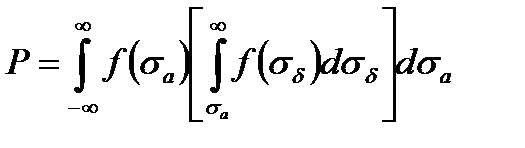или

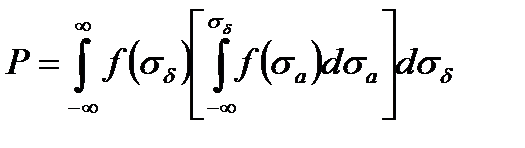
Оценка надежности деталей строительных, дорожных и коммунальных машин по критерию усталости представлена в [1, 6, 7], а металлоконструкций этих машин в [2, 8].

Пример.

Прочность элемента конструкции имеет нормальное распределе­ние с параметрами 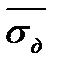= 100 МПа и S_δ =10 Мпа. В процессе обкатки технического средства в элементе возникают напряжения по экспо­ненциальному распределению с математическим ожиданием 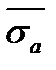=50 Мпа. Определить вероятность безотказной работы элемента.

Решение.

Для решения задачи воспользуемся формулой

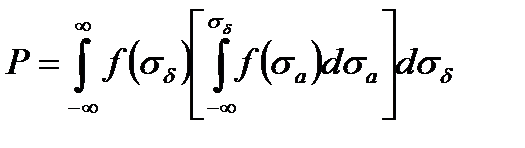
Плотность нормального распределения прочности имеет вид

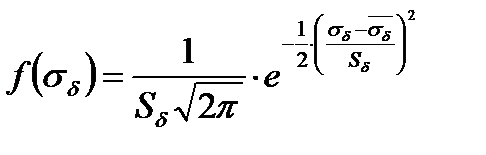
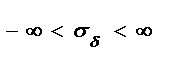
а плотность экспоненциального распределения напряжения имеет

вид

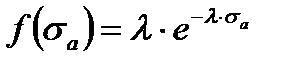
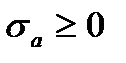
Тогда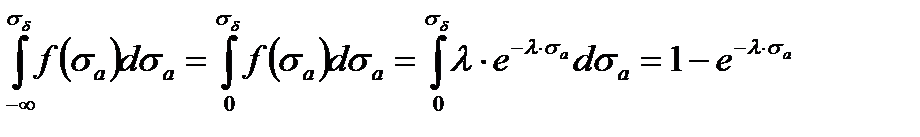

В результате имеем

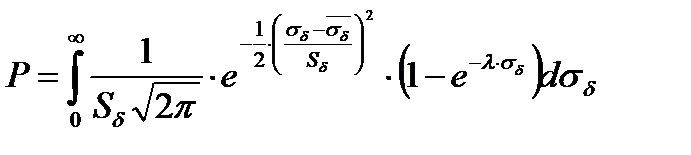
После решения интеграла и преобразований имеем

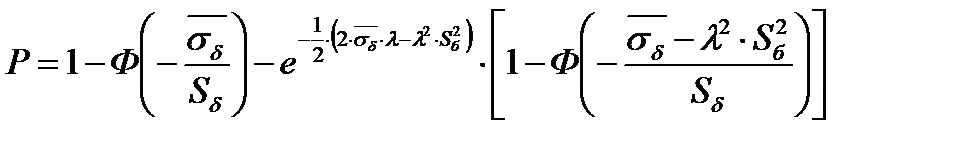
Подставим исходные данные задачи с учетом того, что при экспоненциальном распределении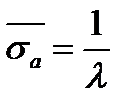

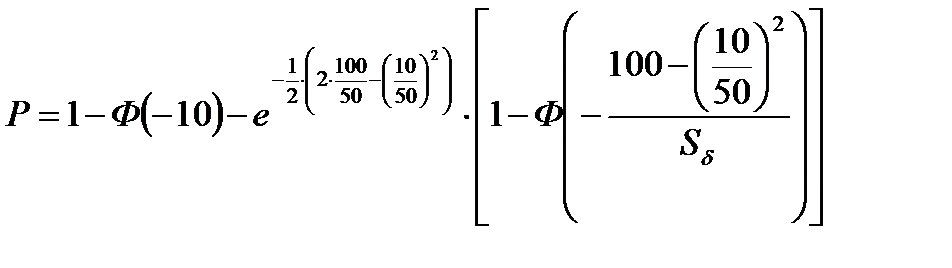
Р=1 - 0,0 – е^-1,98×(1 - 0,0) = 1 - 0,13606 = 0,86194

Оценка надежности при механическом изнашивании

Износостойкость элементов характеризуют интенсивностью изна­шивания I, равной толщине изношенного слоя на единицу пути трения. Линейный износ детали W определяют в зависимости от интенсивно­сти изнашивания, скорости относительного перемещения трущихся поверхностей V и времени работы t по формуле [1]

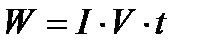
Вероятность безотказной работы по критерию изнашивания опре­деляется по квантилю нормального распределения (табл 1.), равному

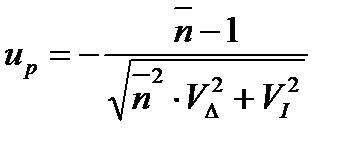
где 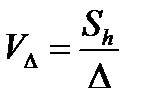- коэффициент вариации размера детали;

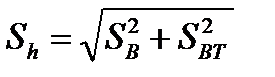- среднее квадратическое отклонение начального зазора, где S_B, S_BT - средние квадратические отклонения диаметров вала и втулки, принимаемые равными шестой части соответствующих допусков;

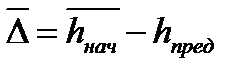- среднее предельно допустимое уменьшение

размера, где h _нач - среднее значение начального зазора, h_пред - предельно допустимый зазор, а в случае увеличения (например, зазора) ;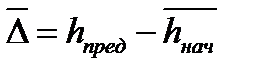

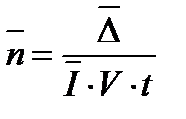- условный коэффициент запаса по износу, где I - среднее значение интенсивности износа;

V- коэффициент вариации интенсивности изнашивания.

Пример

Оценить вероятность безотказной работы Р по критерию износа наконечника рыхлителя вечно мерзлых грунтов при следующих исход­ных данных. Первоначальная длина наконечника 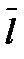=330 мм, пре­дельный износ до длины l = 240 мм, среднее значение интенсивности износа 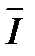= 7-10^-3 мм/м, скорость относительного перемещения тру­щихся поверхностей V = 1 м/с, время работы t= 3 ч, коэффициент ва­риации интенсивности изнашивания v_I = 0,25, коэффициент вариации размера детали v_Δ= 0,01.

Решение

1. Вычисляем среднее предельно допустимое уменьшение раз­мера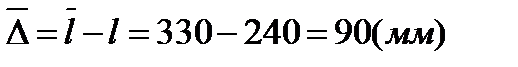

2. Определяем условный коэффициент запаса по износу

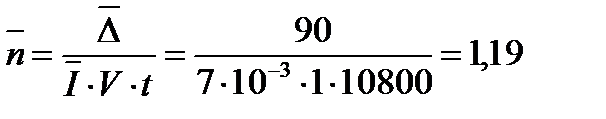
3. Вычисляем квантиль нормального распределения

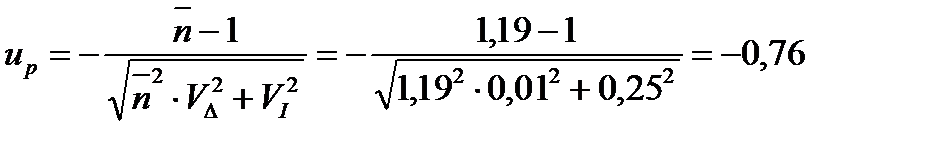
4. По величине полученного значения квантиля, используя таблицу 1, находим вероятность безотказной работы рыхлителя в течение 3 часов.

Р = 0,776 .

Задачи

1. Элемент металлоконструкции дорожной машины подвергает­ся нагрузке, изменяющейся по закону нормального распределения, прочность материала этой детали имеет нормальное распределение с математическим ожиданием 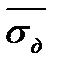= 110 Мпа и средним квадратическим отклонением S_δ=10 Мпа. . Вероятность безотказной работы этой де­тали должна быть Р = 0,99. Определить уровень математического ожидания напряжения 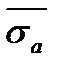воспринимаемого деталью, если коэффи­циент вариации рабочих нагрузок равен V_a=0,25.

2. Прочность материала детали 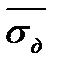=105 Мпа, среднее квадратическое отклонение S_δ= 7,5 Мпа. Нагрузка, воспринимаемая деталью, характеризуется следующими параметрами: 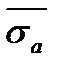=80 Мпа, S_a=20 Мпа. Вычислить вероятность безотказной работы детали, если прочность и напряжение нагрузки имеют: а) логарифмически нор­мальное распределение; б) нормальное распределение.

3. Определить необходимый коэффициент запаса прочности для обеспечения надежности изделия по прочности Р=0,99. Для ре­шения поставленной задачи воспользуйтесь исходными данными за­дач №1 и №2.

ЛИТЕРАТУРА

1. Строительная механика и металлоконструкции строительных и дорожных машин: Учеб. для вузов по специальности "Строительные и дорожные машины и оборудование" /Н.Н. Живейнов, Г.Н. Карасев, И.Ю. Цвей. - М.: Машиностроение, 1988. -280с.

2. Справочник конструктора дорожных машин. Изд. 2-е перераб. и доп./ Под ред. д-ра техн. Наук, проф. И.П. Бородачева. М.: Машино­строение, 1973. -504 с.

3. Хола Исса Абдул Хади. Методика выбора эквивалентной рас­четной схемы для металлоконструкции землеройно-транспортых ма­шин: Дисс., канд. техн. наук/МАДИ: М., 1975. 121с.

4. Исследование и разработка рекомендаций по совершенство­ванию конструкции бульдозера на базе анализа показателей надеж­ности в эксплуатации: Отчет о НИР/МАДИ; №75025167. М., 1976. 271 с.

5. Тракторы: Теория: Учеб. для студентов вузов по спец. «Авто­мобили и тракторы»/ В.В. Гуськов, Н.Н. Велев, Ю.Е. Атаманов, и др; Под общ. ред. В.В.Гуськова. - М. : Машиностроение , 1988

6. Карасев Г.Н. Расчет предельных нагрузок пневмоколесного тя­гача II Строительные и дорожные машины. 2002. № 4. С. 36-41.

7. Гоберман Л.А. Основы теории, расчета и проектирования строительных и дорожных машин: Учеб. для техникумов. М.: Машино­строение, 1988. -464 с.

8. Холодов A.M. Основы динамики землеройно-транспортных машин, М.: Машиностроение, 1968, -156 с.

9. Волков Д.П. Динамика и прочность одноковшовых экскавато­ров, М.: Машиностроение, 1965.-463 с.

10. Решетов Д.Н. и др. Надежность машин: Учеб. пособие для машиностр. спец. вузов/Д.Н. Решетов, А.С. Иванов, В.З. Фадеев; Под ред. Д.Н. Решетова. - М.: Высш. школа, 1988. 238 с.

11. Болотин В.В. Прогнозирование ресурса машин и конструкций. М.: Машиностроение, 1984. -312 с.

12. Эксплуатация дорожных машин: Учебник для вузов / А.М. Шейнин, Б.И. Филиппов, В.А. Зорин и др.; Под ред. A.M. Шейнина. - М.: Транспорт, 1992. 328 с.

13. К.Капур, Л.Ламберсон. Надежность и проектирование систем. -М.: Мир, 1980. -604 с.

14. Волков Д.П., Николаев С.Н. Надежность строительных машин и оборудования. Учеб. пособие для студентов вузов. - М.: Высш. шко­ла, 1979. -400с.

1. Надежность строительных и дорожных машин. - 2-е изд. М,: Машиностроение, 1979.
2. Федоров Д.И., Бондарович Б.А. Надежность рабочего обору­дования землеройных машин. - М.: Машиностроение. 1981. -280 с.
3. Демидчик Н.Н. Разработка автоматизированной системы вы­бора материалов несущих конструкций дорожно-строительных машин / автореферат дисс. канд. техн. наук-М.: МАДИ 1993.
4. Васильев В.В. Механика конструкций из композиционных ма­териалов. - М.: Машиностроение, 1988.