Методы получения интервальных оценок
1). Понятие о доверительном интервале.
2). Интервальная оценка для МОЖ и дисперсии
3). Понятие о доверительном интервале.
В силу случайности точечной оценки “ 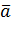 ”всегда актуален вопрос о том, к каким ошибкам может привести практическое использование этой оценки, т.е. вопрос о ее точности и надежности.
”всегда актуален вопрос о том, к каким ошибкам может привести практическое использование этой оценки, т.е. вопрос о ее точности и надежности.
Для ответа на этот вопрос в математической статистике пользуются так называемыми интервальными оценками, в основе которых лежат понятия доверительного интервала и доверительной вероятности.
Пусть для параметра «а» получена из опыта оценка « 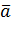 ». Мы хотим оценить ошибку от замены “
». Мы хотим оценить ошибку от замены “ 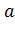 ” на “
” на “ 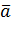 ”. Для этого назначим некоторую достаточно большую вероятность
”. Для этого назначим некоторую достаточно большую вероятность 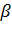 (например
(например 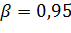 ) такую, что событие с вероятностью
) такую, что событие с вероятностью 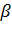 можно считать практически достоверным, и найдем такое значение “
можно считать практически достоверным, и найдем такое значение “ 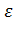 ”, для которого
”, для которого
Вер ( 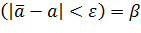 … ..(8.1)
… ..(8.1)
Тогда диапазон практических возможных значений ошибки, возникающий при замене «а» на « 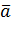 », будет ±
», будет ± 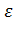 . Большие по абсолютной величине ошибки будут проявляться только с малой вероятностью
. Большие по абсолютной величине ошибки будут проявляться только с малой вероятностью 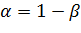 .
.
Зависимость (8.1) можно представить в виде:
Вер 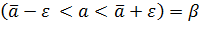 … ..(8.2)
… ..(8.2)
Равенство (8.2) означает, что неизвестное значение параметра «а» с вероятностью 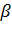 попадает в интервал:
попадает в интервал:
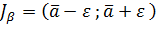 ……(3)
……(3)
Как видно, положение этого интервала на оси «а» является случайным, т.к. случаен его центр « 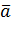 »:
»:

Случайна вообще и длина интервала “ 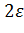 ”, т.к. “
”, т.к. “ 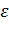 ” вычисляется, как правило, по опытным данным.
” вычисляется, как правило, по опытным данным.
Поэтому правильнее толковать величину 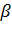 не как вероятность попадания точки «а» в интервал
не как вероятность попадания точки «а» в интервал 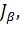 а как вероятность того, что случайный интервал
а как вероятность того, что случайный интервал 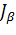 накроет точку «а».
накроет точку «а».
Вероятность 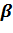 называется доверительной вероятностью, а интервал
называется доверительной вероятностью, а интервал 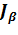 – доверительным интервалом. Границы интервала
– доверительным интервалом. Границы интервала 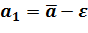 и
и 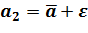 называются доверительными границами.
называются доверительными границами.
Доверительный интервал можно рассматривать как интервал значений неизвестного параметра «а», совместных с опытными данными и не противоречащих им. Действительно, если считать события с вероятностью 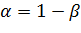 практически невозможными, то те значения «а» для которых
практически невозможными, то те значения «а» для которых 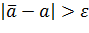 , нужно признать противоречащими опытным данным, а те, для которых
, нужно признать противоречащими опытным данным, а те, для которых 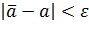 , - совместимыми с ними.
, - совместимыми с ними.
Для нахождения доверительных границ 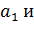
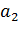 можно использовать как точные, так и приближенные методы. Рассмотрим эту процедуру на примере точных методов применительно к интервалам для математического ожидания и дисперсии.
можно использовать как точные, так и приближенные методы. Рассмотрим эту процедуру на примере точных методов применительно к интервалам для математического ожидания и дисперсии.
Интервальная оценка для МОЖ и дисперсии.
Пусть 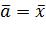 , т.е. имеем оценку для неизвестного математического ожидания
, т.е. имеем оценку для неизвестного математического ожидания 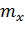 случайной величины “x”. Как правило, дисперсия также неизвестна, так что вместо
случайной величины “x”. Как правило, дисперсия также неизвестна, так что вместо 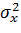 надо использовать
надо использовать 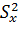 .
.
Тогда :
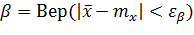
Перейдем к правой части этого равенства от случайной величины  к случайной величине T, распределенной по закону Стьюдента. Для этого умножим обе части неравенства, содержащегося в скобках, на положительную величину
к случайной величине T, распределенной по закону Стьюдента. Для этого умножим обе части неравенства, содержащегося в скобках, на положительную величину 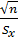 :
:
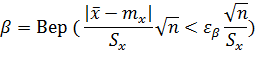
или
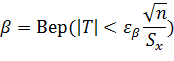
Теперь найдем такое число 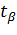 , для которого справедливо равенство:
, для которого справедливо равенство:
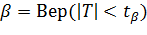
Но: Вер ( 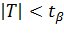 ) =
) = 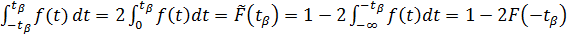
т.к. функция 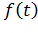 – четная.
– четная.
Следовательно:
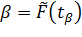 ,
,
откуда 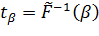 ,
,
полагая 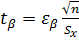 ,
,
находим 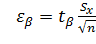 .
.
Таким образом :
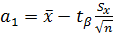 и
и 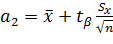
Пример
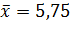 ; ;
| n =25 | 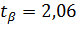
|
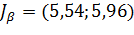
|
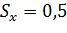 ; ;
| 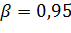
| 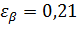
| |
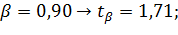 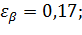 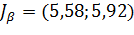
|
Вывод: Чем выше уровень доверительной вероятности, тем шире доверительный интервал!
Аналогичным образом можно определить доверительный интервал для дисперсии, если 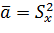 . Для этого достаточно воспользоваться V-статистикой, имеющей
. Для этого достаточно воспользоваться V-статистикой, имеющей 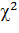 -распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
-распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
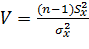 ,
,
откуда 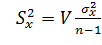
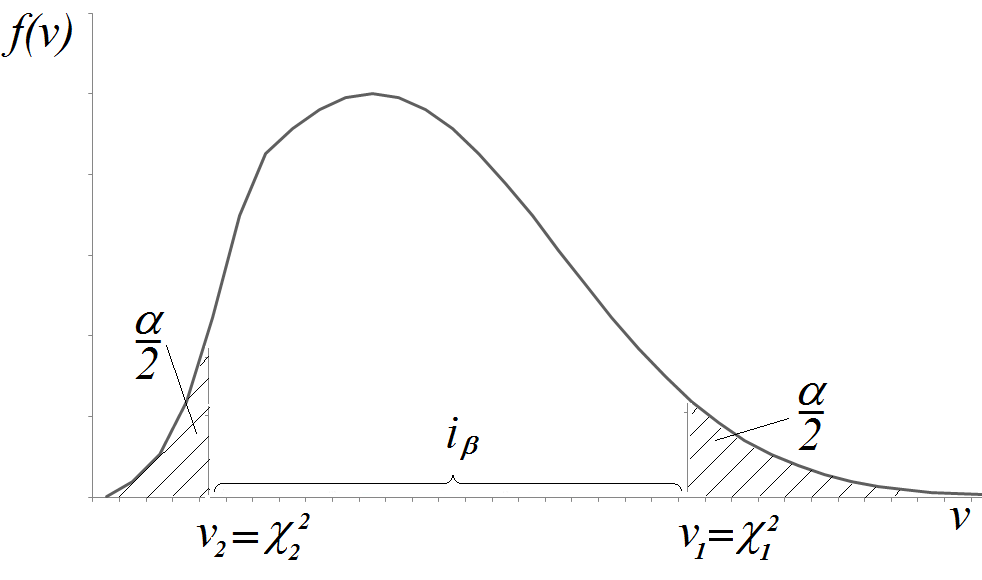
Как видно из рисунка, закон распределения статистики V в отличие от закона распределения статистики T не является симметричным. Поэтому возникает вопрос: как выбрать интервал 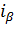 , в который величина V=
, в который величина V= 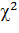 попадает с вероятностью
попадает с вероятностью 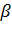 ?
?
Условимся выбирать интервал 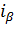 так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
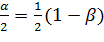 .
.
Чтобы построить интервал 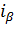 с таким свойством надо воспользоваться таблицей, в которой приведены числа
с таким свойством надо воспользоваться таблицей, в которой приведены числа 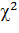 такие, что
такие, что
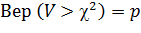 .
.
Зафиксировав ν = n-1, находят по таблице два значения 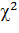 :
:
Одно 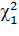 , отвечающие вероятности
, отвечающие вероятности 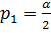 , и другое
, и другое 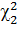 , отвечающее вероятности
, отвечающее вероятности 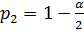 . Очевидно, что интервал
. Очевидно, что интервал 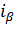 имеет
имеет 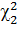 своим левым, а
своим левым, а 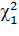 - правым концом.
- правым концом.
Теперь по интервалу 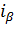 найдем искомый интервал
найдем искомый интервал 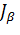 для неизвестной дисперсии
для неизвестной дисперсии 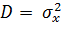 с границами
с границами 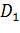 и
и 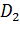 , который накрывает точку D с вероятностью
, который накрывает точку D с вероятностью 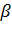 :
:
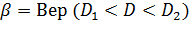
Для этого убедимся в равносильности неравенств:
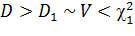
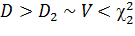 ,
,
Откуда:
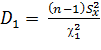 и
и 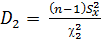
Пример:
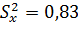
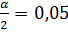
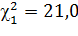
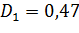
n =13 ν = 12 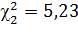
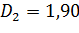
Если интегрировать слева направо:
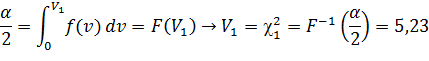
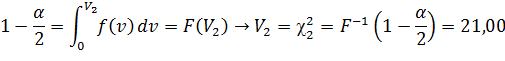
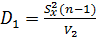
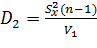
Дата добавления: 2022-05-27; просмотров: 174;











