Статистические гипотезы о дисперсиях
Сравнение дисперсии с нормативом
На основе выборки объемом n получено значение статистической дисперсии
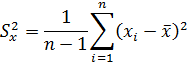
Задано нормативные значение 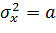 . Подлежит проверке система гипотез:
. Подлежит проверке система гипотез: 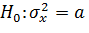 против
против 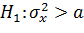 .
.
Рекомендуемая статистика
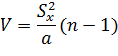
имеет 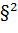 - распределение с
- распределение с 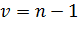 . Проверка по общей схеме.
. Проверка по общей схеме.
Пример
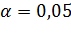
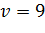
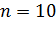
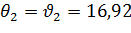
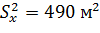
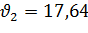
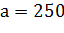
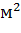 Но отклоняется
Но отклоняется
Сравнение двух дисперсий
Имеются две нормально распределенные совокупности с неизвестными дисперсиями  . На основе выборок из этих совокупностей получены оценки
. На основе выборок из этих совокупностей получены оценки 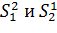 , примем
, примем 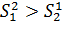 . Объемы выборок
. Объемы выборок 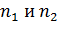 соответственно. Подлежит проверке система гипотез:
соответственно. Подлежит проверке система гипотез:
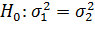 против
против 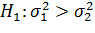 .
.
Рекомендуемая статистика – статистика Фишера:
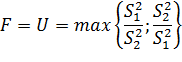
Для малых и средних выборок эта статистика подчинена F – распределению со степенями свободы 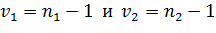 , если
, если 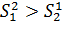 , и
, и 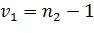 ,
, 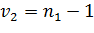 , если
, если 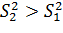 . Ее плотность имеет вид:
. Ее плотность имеет вид:
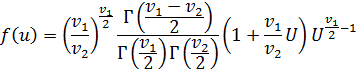
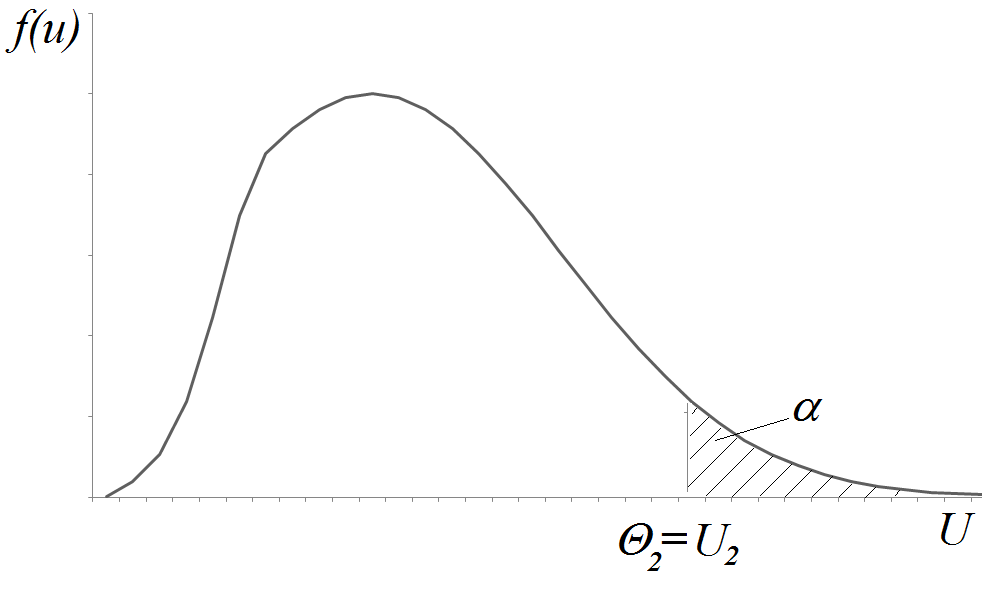
Пример
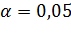
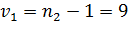
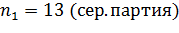
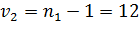
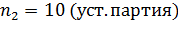
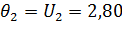
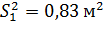
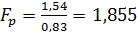
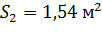 Но принимается
Но принимается
Оценивание свойств изделий по результатам испытаний.
1). Виды оценок параметров законов распределений и числовых характеристик случайных величин. Требования к точечным оценкам.
2). Методы получения точечных оценок
Виды оценок параметров законов распределений и числовых характеристик случайных величин. Требования к точечным оценкам.
Основным результатом любых испытаний являются опытные данные, характеризирующие какие-либо свойства объекта. В большинстве случаев показателями оценки этих свойств являются случайные величины. Исчерпывающей характеристикой любой случайной величины является, как известно, закон распределения вероятностей проявления ее возможных значений. В свою очередь, закон распределения, как правило, содержит некоторые постоянные величины, именуемые параметрами. В зависимости от числа параметров законы подразделяются на одно- и много- параметрические. Если параметры закона заранее неизвестны, то они подлежат определению по результатам испытаний.
Известно также, что кроме законов распределения случайные величины принято оценивать так называемыми числовыми характеристиками, под которыми подразумевают величины, характеризующие отдельные свойства случайных величин. Чаще всего на практике используются характеристики положения (математические ожидания, мода, медиана) и моменты различных порядков (дисперсия, асимметрия, эксцесс). Числовые характеристики, как и параметры законов, также подлежат определению по результатам испытаний.
Таким образом, оценивание свойств любого объекта связано с определением на основе опытных данных либо параметров законов распределения, либо числовых характеристик случайных величин.
Но число опытов всегда ограничено. Поэтому любое значение искомого параметра или характеристики всегда будет содержать элемент случайности, то есть является приближением.
Приближенное значение параметра закона распределения или числовой характеристики случайной величины, полученной на основе опытных данных, называется оценкой.
Примеры оценок числовых характеристик случайных величин Х:
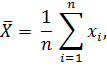
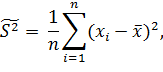
Где 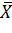 – оценка математического ожидания mx,
– оценка математического ожидания mx,
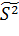 – оценка дисперсии
– оценка дисперсии 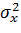
В общем случае оценку параметра при характеристике 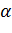 будем обозначать через
будем обозначать через 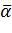 .
.
Оценки подразделяются на точечные и интервальные.
Точечные оценки, как в приведенных примерах, однозначно определяют оцениваемый параметр или характеристику, в то время как интервальные определяют некоторый диапазон возможных значений неизвестной величины 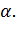 Интервальные оценки отличаются большей информативностью, нежели точечные.
Интервальные оценки отличаются большей информативностью, нежели точечные.
К точечным оценкам предъявляются три основных требования: точечная оценка должна быть состоятельной, несмещенной и эффективной.
Состоятельность оценки означает ее сходимость по вероятности к величине 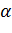 при неограниченном возрастании числа опытов:
при неограниченном возрастании числа опытов:
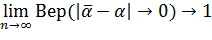
Несмещенность оценки предполагает отсутствие систематической ошибки при замене неизвестной величины  на приближенную
на приближенную 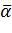 :
:
M [ 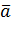 ] =
] = 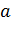
В приведенных примерах:
M [  ] = mx ;
] = mx ;
M [ 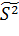 ] =
] = 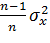 .
.
Поэтому вместо 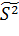 надо использовать S2 =
надо использовать S2 = 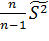
Тогда
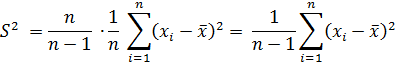
Эффективность оценки означает, что выбранная оценка обладает наименьшей дисперсией по сравнению с другими возможными оценками:
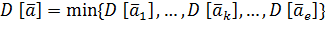
Методы получения точечных оценок.
Различают аналитические и графические методы получения точечных оценок. Рассмотрим первую группу методов. Она включает в себя: метод моментов, метод квантилей и метод максимума правдоподобия.
Метод моментов
Сущность метода заключается в том, что теоретические моменты, зависящие от неизвестных параметров закона распределения, приравниваются к эмпирическим. Основанием для этого является то обстоятельство, что если число опытов достаточно велико, то опытные значения моментов близки к теоретическим:
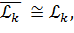
Где 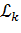 – теоретическое значение начального момента k-ого порядка,
– теоретическое значение начального момента k-ого порядка,
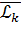 – эмпирическое значение начального момента k-ого порядка.
– эмпирическое значение начального момента k-ого порядка.
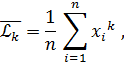
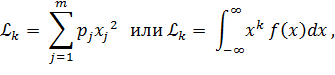
n – объем выборки,
m – число возможных значений дискретной случайной величины.
Пример. Случайная величина Х распределена по экспоненциальному закону с неизвестным параметром 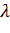 . Требуется на основе опытных данных найти оценку
. Требуется на основе опытных данных найти оценку  .
.
Решение:
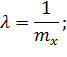
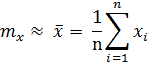
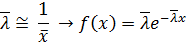
Метод моментов рекомендуется использовать при n>30.
Метод квантилей
Сущность метода заключается в том, что неизвестные значения теоретической функции распределения приравнивается к известным эмпирическим значениям (частотам) для одной и той же квантили x*
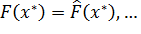
Где 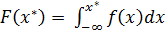 - значение теоретической функции распределения для x=x* ;
- значение теоретической функции распределения для x=x* ;
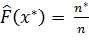 - значение эмпирической функции распределения для x=x*,
- значение эмпирической функции распределения для x=x*,
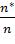 - накопленная частота, соответствующая разряду, в котором находится x*
- накопленная частота, соответствующая разряду, в котором находится x*
n*- число опытных данных (измерений), попавших в разряд, соответствующий x*.
Число таких уравнений должно быть равно числу неизвестных параметров в законе распределения.
Пример. В условиях предыдущего примера найти оценку  , используя метод квантилей. Решение:
, используя метод квантилей. Решение:
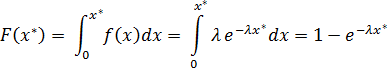
Полагаем 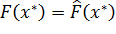 , в силу чего
, в силу чего 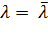 :
:
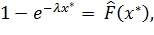
Откуда 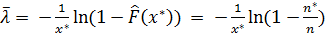
Метод квантилей более универсален относительно объема выборки, нежели метод моментов. Но оценки, получаемые с его помощью, обладают значительной дисперсией.
Метод максимума правдоподобия
Этот метод является общим способом определения оценок параметров закона распределения по выборке Xn = {x1, ….,xI, …., xn}. Пусть имеем случайную величину X с плотностью распределения f(x,a), где a={a1, ….,aj, …., am} – вектор параметров. Вероятность получения на опыте выборки Xn на интервале xi+  xi:
xi:
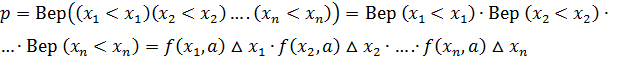
Т.к. выборка Xn наблюдалась на опыте, то логично полагать P=Pmax и, исходя из этого, искать неизвестные оценки  .
.  Для удобства практических расчетов зависимость для P преобразуют, а именно: вводят в рассмотрение так называемую функцию правдоподобия
Для удобства практических расчетов зависимость для P преобразуют, а именно: вводят в рассмотрение так называемую функцию правдоподобия
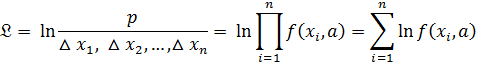
Тогда искомые оценки  можно определить из системы уравнений
можно определить из системы уравнений
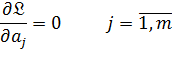
Пример. В условиях предыдущего примера найти оценку  , используя метод максимума правдоподобия. Решение:
, используя метод максимума правдоподобия. Решение:
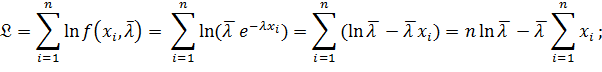
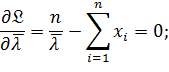
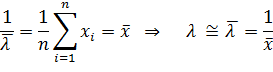
Дата добавления: 2022-05-27; просмотров: 164;











