Проверка статистических гипотез о числовых характеристиках случайных величин
1). Статистические гипотезы о средних.
2). Статистические гипотезы о дисперсиях.
Статистические гипотезы о средних
Различают два основных типа гипотез о средних: сравнение среднего со стандартом (нормативом) и сравнение средних нескольких (в простейшем случае двух) совокупностей.
Сравнение средней со стандартом. Пусть имеем выборку 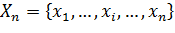 , полученную по результатам испытаний. На ее основе определено среднее:
, полученную по результатам испытаний. На ее основе определено среднее:
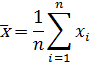
Задано нормативное значение среднего – величина «а».
Подлежит проверке гипотеза:
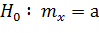
при 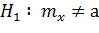
Для случая большой выборки (n>30) и известной дисперсии 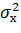 величина
величина 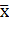 подчинена нормальному распределению с параметрами:
подчинена нормальному распределению с параметрами:

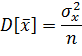
Поэтому в качестве статистики целесообразно выбрать величину
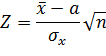
Известно:
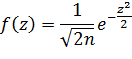
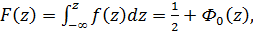 где
где
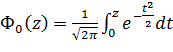 - интеграл вероятностей
- интеграл вероятностей
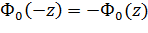
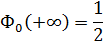
1. Проверка гипотез о средних:
1.1 Сравнение средней с нормативом
| 1) | 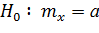

| 2) | 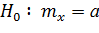
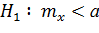
| 3) | 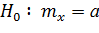
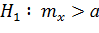
|
Для всех вариантов – два случая: 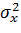 известна и
известна и 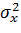 неизвестна, т.е. используется
неизвестна, т.е. используется 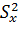 . В первом случае используется Z- статистика, во втором – T- статистика. Порядок нахождения критических точек:
. В первом случае используется Z- статистика, во втором – T- статистика. Порядок нахождения критических точек:
Z- статистика
Двусторонняя КО
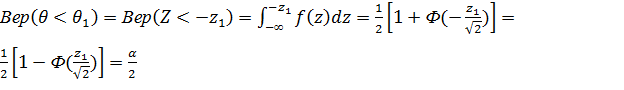 ;
;
 ;
;
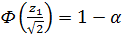 ;
;
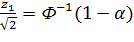 ;
;
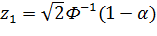 ;
;
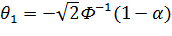 ;
;
 .
.
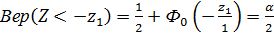 ;
;
 ;
;
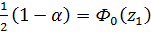 ;
;
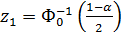 ;
;
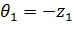 ;
; 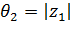 .
.
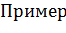 :
: 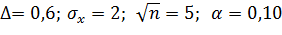
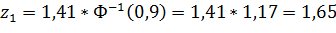
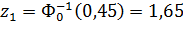
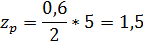
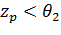 Но принимается
Но принимается
Односторонняя КО
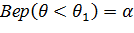 ;
;
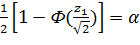 ;
;
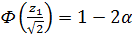 ;
;
 ;
;
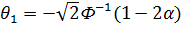 ;
;
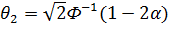
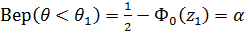 ;
;
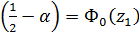 ;
;
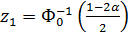 ;
;
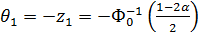 ;
;
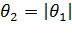 .
.
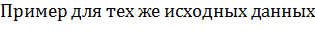 :
:
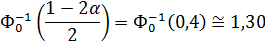
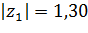
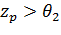 Но отклоняется
Но отклоняется
Вывод: Односторонний критерий является более жестким.
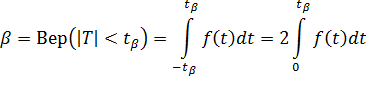
OKO: 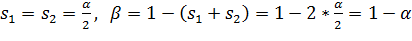 ;
;
ДКО: 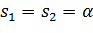 ,
, 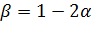 .
.
T- статистика
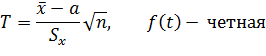
В силу четности f(x) табулируется не F(t), а функция 
Пример: 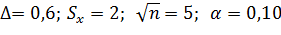
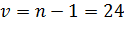
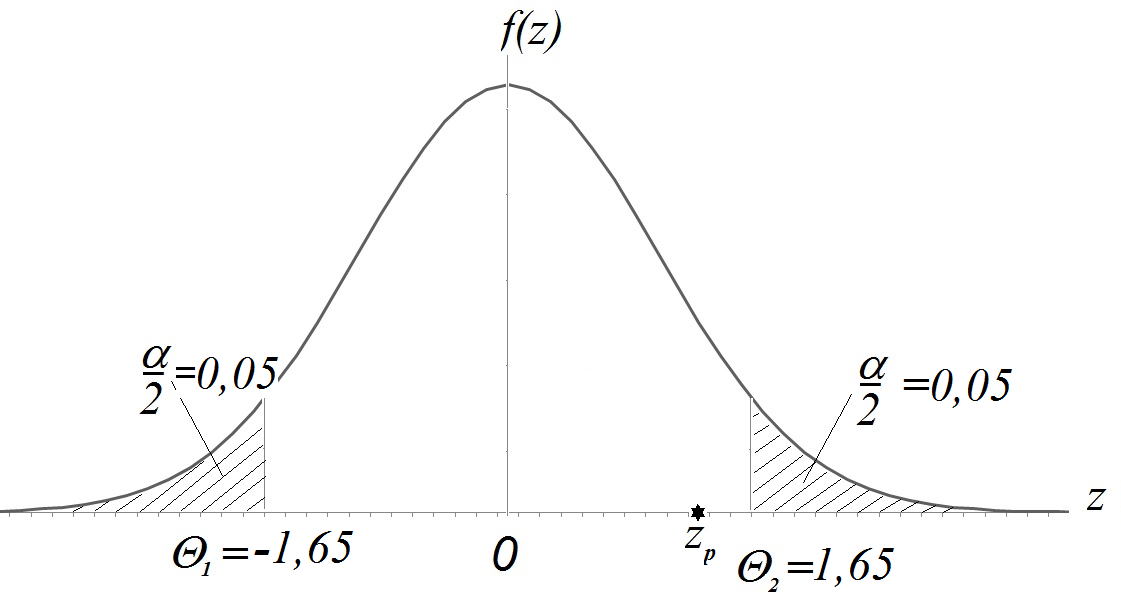
Для ДКО: 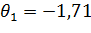 ;
; 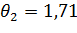 ;
;
Для ЛКО: 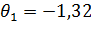 ;
;
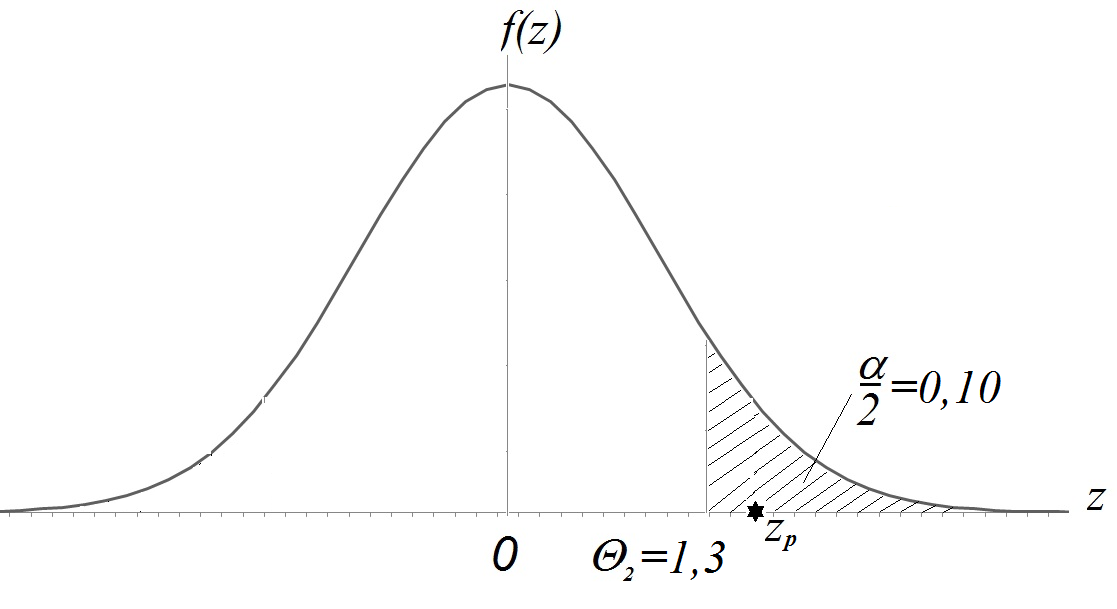
Для ПКО: 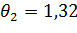 ;
;
Т.к. 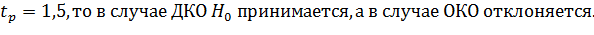
Для сравнения:
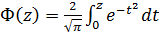 - интеграл ошибок (erf(z)) или функция Лапласа
- интеграл ошибок (erf(z)) или функция Лапласа
Ф(-z) = -Ф(z)
Ф 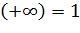
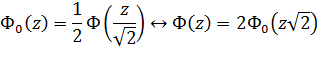
F(z) = 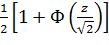
При альтернативе 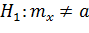 критическая область будет двусторонней:
критическая область будет двусторонней:
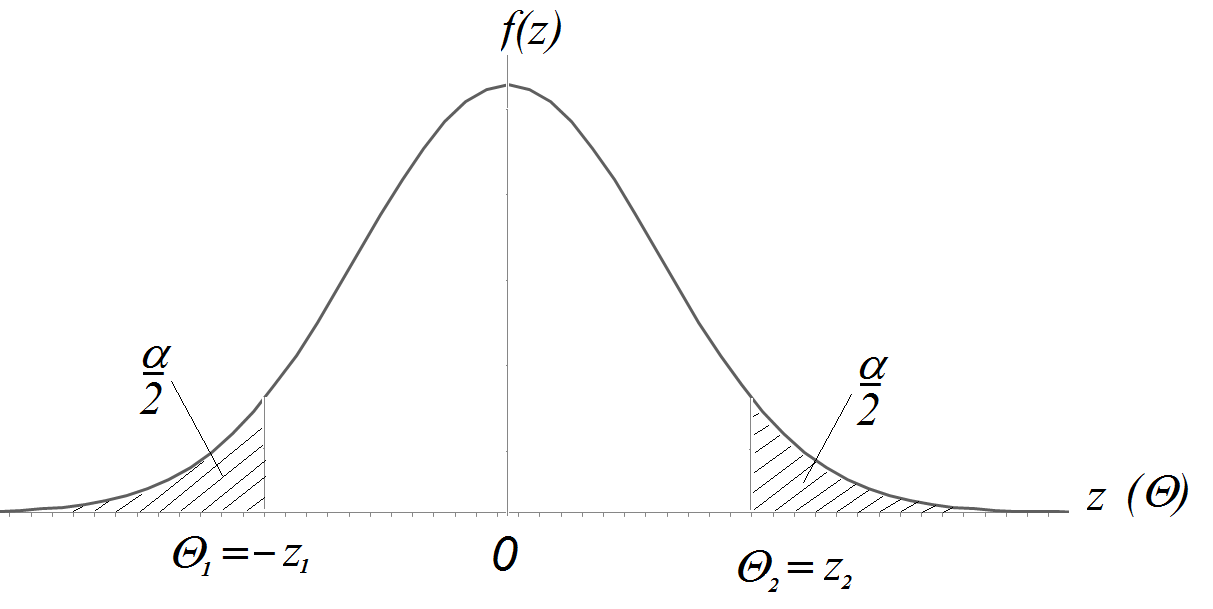
Значение критических точек 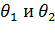 определяется из уравнений:
определяется из уравнений:
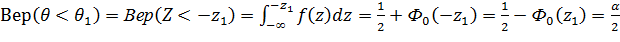 ;
;
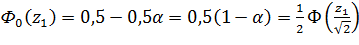 ;
;
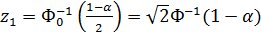 .
.
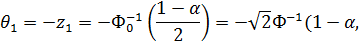
где 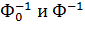 есть функции Лапласа
есть функции Лапласа
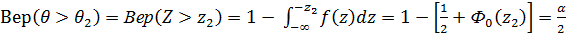 ;
;
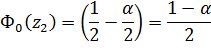
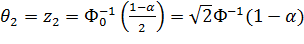 .
.
При альтернативе  критическая область будет правосторонней и точка
критическая область будет правосторонней и точка 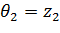 определится из уравнения:
определится из уравнения:
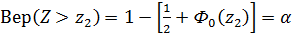 ,
,
 .
.
Соответственно для 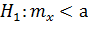 имеем левостороннюю область и
имеем левостороннюю область и
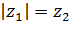
Пример 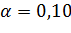
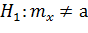
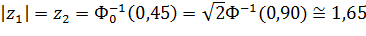

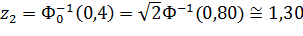
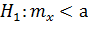
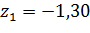
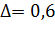
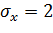
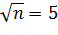
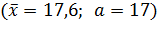
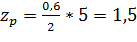
| 
|
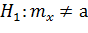 Но принята Но принята
|  Но отклоняется Но отклоняется
|
Вывод: Односторонний критерий является более жестким, чем двусторонний.
Если дисперсия  известна, то используют статистику
известна, то используют статистику
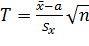 ,
,
где 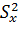 - статистическая дисперсия:
- статистическая дисперсия:
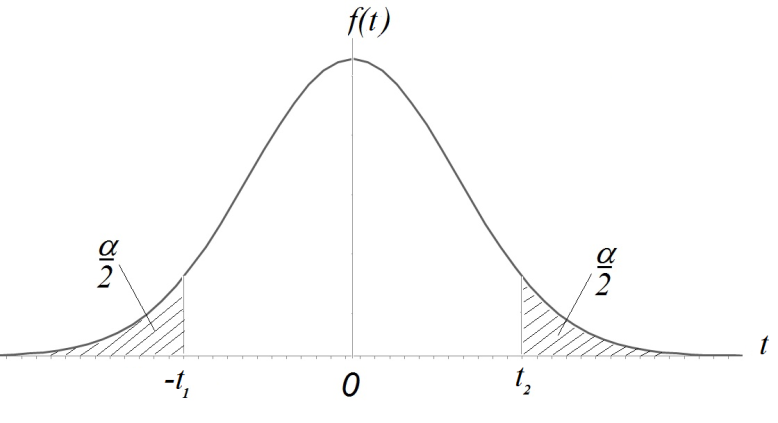
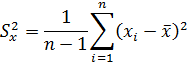
Известно: 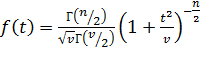 , где v = n-1
, где v = n-1
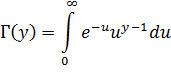
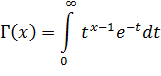
Функция квавантилей для t–распределения рассчитана (затабулирована) на основе зависимости:
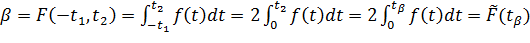 ,
,
где 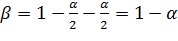
Поэтому:
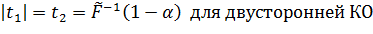 и
и
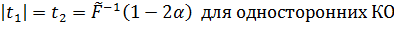
Пример
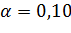
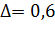

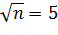 v = 24
v = 24
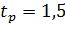
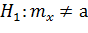
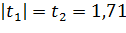 Но принимается
Но принимается
| 
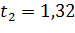 Но отклоняется
Но отклоняется
|
Сравнение средних двух совокупностей
Пусть имеются две выборки объемом 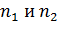 соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних
соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних 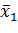 и
и  . Требуется проверить гипотезу
. Требуется проверить гипотезу  . Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
. Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
Первый вариант: дисперсии выборок 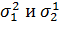 известны и равны друг другу, а так же
известны и равны друг другу, а так же 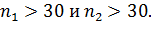 Рассмотрим разность
Рассмотрим разность 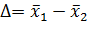 . Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза
. Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза 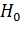 верна:
верна:
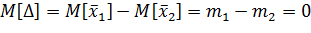
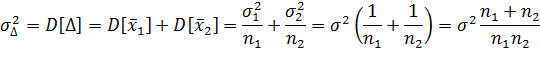
Выберем в качестве статистики величину
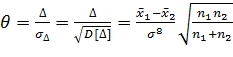 ; D[
; D[ 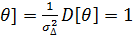
Если 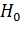 верна, то M[
верна, то M[ 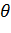 ], и D[
], и D[ 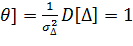 , т.е.
, т.е.  и поэтому дальнейшая проверка ведется по общей схеме.
и поэтому дальнейшая проверка ведется по общей схеме.
Второй вариант: выборки малы ( 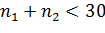 ),
),  неизвестны, то можно полагать (есть основания)
неизвестны, то можно полагать (есть основания) 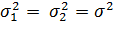 .
.
Тогда определяют общую (двух выборок) статистическую дисперсию
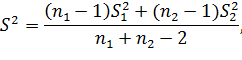
где  – статистические дисперсии выборок.
– статистические дисперсии выборок.
На роль статистики принимают величину
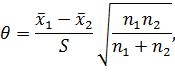
которая подчиняется t- распределению с числом степеней свободы v= 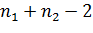 .
.
Дальнейшая проверка ведется по общей схеме.
Третий вариант: 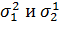 неизвестны и нет оснований полагать их равными, т.е.
неизвестны и нет оснований полагать их равными, т.е.  . Имеем проблему Беренса-Фишера.
. Имеем проблему Беренса-Фишера.
Дата добавления: 2022-05-27; просмотров: 178;











