Частные случаи пересечения поверхностей вращения второго порядка

Пересечение соосных поверхностей вращения.

1. Две соосные поверхности вращения пересекаются по окружностям, плоскости которых перпендикулярны оси вращения: Г Ç D = m; n - окружности (рис. 3-48).

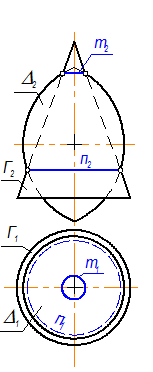
Рис. 3-48

2. Если центр сферы находится на оси поверхности вращения, то сферапересечёт эту поверхность по окружностям, плоскости которых перпендикулярны оси вращения: Ф Ç L = m; n - окружности (рис. 3-49).

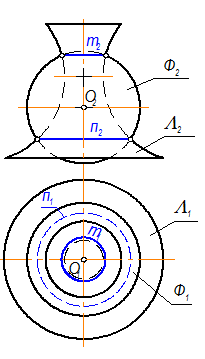
Рис. 3-49

Теорема Монжа

Если две поверхности вращения второго порядка описаны около третьей поверхности вращения второго порядка, или вписаны в неё, то линия их пересечения распадается на две плоские кривые второго порядка. Причём, плоскости кривых проходят через прямую, соединяющую точки двойного соприкосновения.

На рис. 3-50 теорема Монжа проиллюстрирована пересечением двух конусов S и Г, в которые вписана сфера Ф. Чтобы вписать сферу, проводим перпендикуляры к очерковым образующим конуса Г(Г₂) из точки О₂: О₂Р₂ = О₂К₂ - радиус сферы (рис. 3-50а). Точки М и N (рис. 3-50б) - это точки, в которых касаются все три поверхности. В результате получаются два эллипса а и b, которые проходят через точки М и N (рис. 3-50в). На П₁ эти эллипсы построены по принадлежности конусу Г (построения не показаны).

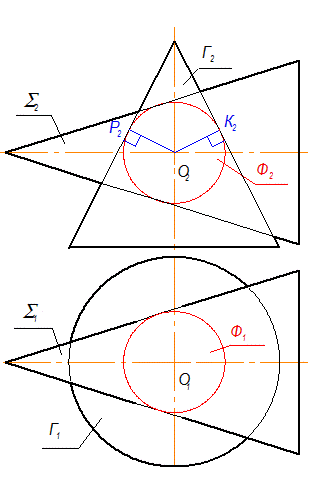
Рис. 3-50а

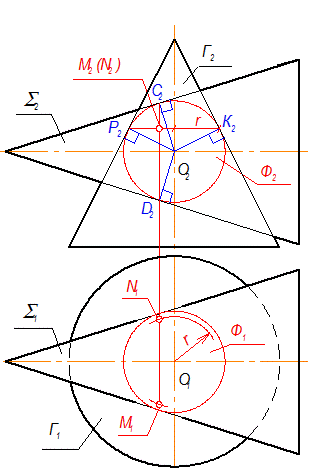
Рис. 3-50б

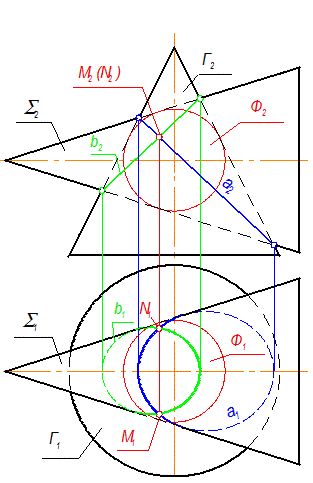
Рис. 3-50в

Как Вы думаете?

1. Всегда ли при решении позиционных задач совпадают случаи расположения геометрических фигур относительно плоскостей проекций и соответствующие алгоритмы решения?

2. По какому алгоритму Вы будете решать задачу , представленную на рис. 51?

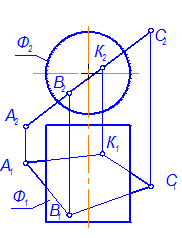
Рис. 3-51

Ф Ç АВСК = ?

Ф ^^ П₂; АВСК ^^ П₂.

Проанализируйте расположение цилиндра и плоскости относительно плоскостей проекций и обоснуйте выбор алгоритма решения. Решите задачу.

Выводы:

1. Все главные позиционные задачи делятся на две:

1ГПЗ - пересечение линии с поверхностью (плоскостью);

2ГПЗ - пересечение поверхностей (плоскостей).

2. Выбор алгоритма решения зависит от расположения фигур относительно плоскостей проекций. Существует три случая расположения пересекающихся фигур относительно плоскостей проекций:

- обе фигуры проецирующие - задача решается по 1 алгоритму,

- одна фигура проецирующая, вторая непроецирующая - задача решается по 2 алгоритму,

- обе фигуры непроецирующие - задача решается по 3 алгоритму.

3. Бывает, что случаи расположения фигур относительно плоскостей проекций и алгоритм решения не совпадают. Это случается тогда, когда обе пересекающиеся фигуры являются проецирующими, но относительно одной и той же плоскости проекций, такие задачи решаются по второму алгоритму (например, рис. 3-51).

4. Решение считается выполненным тогда, когда определена видимость общих элементов и пересекающихся фигур.