Внутреннее строение кристаллов
Связь между формой макро- или микрокристалла и его внутренним строением, определяемым распределением элементарных материальных частиц в пространстве, удалось установить после открытия рентгеновских лучей.
При прохождении через кристалл узкого параллельного пучка рентгеновских лучей наблюдается их дифракция и интерференция (Лауэ, 1912). На регистрирующей фотопластинке кроме центрального пятна появляется большое количество пятен, расположение которых характерно для данного кристалла и угла поворота его к направлению рентгеновского луча.
В 1913 г. У.Г. и У.Л. Брэгги предложили уравнение, связывающее расстояние между плоскостями в кристалле, вызывающими явление интерференции, длину волны рентгеновского луча и угол между направлением луча и плоскостью кристалла
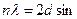 Ө,
Ө,
где λ - длина волны рентгеновского луча, d - расстояние между плоскостями, Ө - угол между лучом и плоскостью или угол скольжения, п - целое число (условие усиления лучей).
Длина волны рентгеновского луча зависит, как известно, от материала антикатода.
Восстановив по фигурам интерференционных пятен расположение в пространстве частиц, вызвавших дифракцию, можно сделать вывод о внутреннем строении кристалла.
Таким образом, внутреннее строение кристаллов представляется как система атомов, определенным образом расположенных в пространстве, - кристаллическая решетка.
Элемент кристаллической решетки или элементарная ячейка - геометрическая фигура, образованная материальными частицами, расположенными определенным образом в пространстве, мысленно выделенная из общего тела кристалла.
Последнее добавление в формулировке необходимо потому, что кристаллическая решетка не представляет собой сумму изолированных кристаллических ячеек (например, кубов), а каждая частица, входящая в данную ячейку, одновременно принадлежит и окружающим ее кристаллическим элементам.
Оказалось, что число форм кристаллических ячеек меньше, чем форм макрокристаллов, так как скорость распространения этих ячеек по осям симметрии может быть различной, что и приводит к построению различных по форме макрокристаллов. Плоская грань кристалла может представлять собой ступенчатую поверхность, образованную слоями кристаллических ячеек, но она кажется нам идеально гладкой, так как высота этих ступенек измеряется ангстремами. Исходя из внутреннего строения кристалла, можно дать другое определение кристаллического тела: кристалл - часть пространства, заполненная параллельной трансляцией геометрического элемента, называемого элементарной ячейкой.
Рассмотрим элементарную ячейку простого куба и определим ее основные характеристики. Важнейшей характеристикой куба является величина его ребра а. Однако не всегда расстояние между его плоскостями d, заполненными материальными частицами и вызывающими дифракцию и интерференцию рентгеновских лучей, равно величине ребра: d = a. В кубе можно провести несколько плоскостей (рис. 32).Их индикация определяется числом пересечений с осями координат: это плоскости 100, 110 и 111. Если рентгеновские лучи падают перпендикулярно плоскости 100 (рис. 33, а), то они встретят 2 плоскости и расстояние между плоскостями будет равно d100; если они перпендикулярны плоскости 110, то d110 = 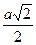 так как плоскостей будет уже 3 и расстояние между плоскостями равно половине диагонали грани куба (рис. 33, б), а если лучи будут падать перпендикулярно плоскости 111, то они встретят уже 4 плоскости и расстояние между этими плоскостями равно d 111 =
так как плоскостей будет уже 3 и расстояние между плоскостями равно половине диагонали грани куба (рис. 33, б), а если лучи будут падать перпендикулярно плоскости 111, то они встретят уже 4 плоскости и расстояние между этими плоскостями равно d 111 = 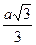 (рис. 33, в).
(рис. 33, в).

Рис. 32. Рентгенографические плоскости
в простой кубической решетке

Рис. 33. Схема встречи рентгеновских лучей
с плоскостями в кристалле кубической системы
Отношение обратных величин d100, d110 и d111 является характеристикой для данного типа кристаллической решетки:
 :
: 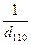 :
:  =1:
=1: 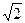 :
: 
Это соотношение, постоянное для данной решетки, в конечном итоге определяет отношение расстояний на рентгенограмме кристалла (рис. 33).
Вторая важная характеристика любой элементарной ячейки - координационное число: координационным числом называется число одинаковых частиц, расположенных на кратчайшем расстоянии от данной частицы (число ближайших соседей). Для простого куба на кратчайшем расстоянии от частицы А равным а расположено 6 частиц, т.е. координационное число K = 6.
Другой характеристикой элементарной ячейки является число частиц, необходимое для ее построения. каждая частица, находящаяся в вершине куба, принадлежит одновременно 8 кубам, сходящимся в одной точке (А), а, следовательно, на данный куб приходится только 1/8 ее часть. Вершин в кубе 8 и для построения данного куба требуется только одна частица: n = (1/8) 8 = 1.
Зная число частиц, необходимых для построения элемента кристаллической решетки, массу этих частиц и плотность кристалла, можно определить сторону куба, а, следовательно, и значения d, входящих в уравнение Брэггов, а это в свою очередь было необходимо для определения длины волны λ рентгеновских лучей, получаемых от различных антикатодов. Если бы этого не было сделано, то Мозли не смог бы открыть свой закон.
В самом деле, зная систему кристаллической решетки и элементарной ячейки, число частиц, необходимое для построения, их массы и плотность кристалла, можно определить все геометрические размеры. Для кубических форм элементарных ячеек эта задача решается наиболее просто.
Если число частиц n, а масса их A/N, где А - атомная масса, а N - число Авогадро, то масса элементарной ячейки будет m = nA/N. Объем элементарной ячейки выразим через плотность кристалла ρ, и он будет равен кубу стороны:
υ = (nA/ρN) = a3. Отсюда величина ребра куба
a= 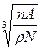
Элементарный куб - тип NaCl, n = l; K = 6, но так как в узлах элементарной ячейки находятся ионы Na+ и ионы Сl-, то это необходимо учесть: n = (l/8) 4Na++ (l/8) 4Cl- = (l/2) NaCl, т.е. требуется половина молекулы для построения ячейки
a = 
Плотность кристалла NaCl ρ = 2,164∙103 кг/см3; MNaCl = 58,5 кг/кмоль; число Авогадро N = 6,02∙1026кмоль-1. Подставляем данные в уравнение и получаем
 =2,814 Ǻ
=2,814 Ǻ
Объемноцентрированный куб - тип CsCl. В этом случае К = 8; n = (1/8) 8+1 = 2. При построении ячейки также нужно учесть, что в узлах элементарной ячейки находятся ионы Cs+ и Сl-. Тогда Cs+ + Cl- = CsCl или уравнение для этого случая будет
а = 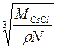
Дата добавления: 2016-12-09; просмотров: 1958;











