Энергия взаимодействия дискретных зарядов

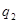Если есть два заряда и , то 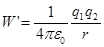- энергия, которую необходимо затрать для разведения двух зарядов с расстояния 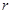до . Если 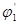- потенциал второго заряда в центре первого, и аналогично , тогда энергия взаимодействия

,

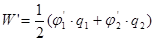или же энергия взаимодействия системы зарядов:

.

Если же распределение зарядов непрерывное, и в 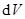содержится 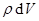зарядов, тогда

.

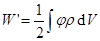Если же заряды находятся как в объеме, так и на поверхности, то

.

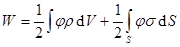Энергия заряженных проводников

На проводниках – только поверхностные заряды, поэтому

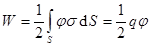, или же

.

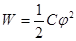Плотность энергии электромагнитного поля

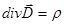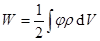, , где 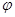- потенциал в .

, .

.

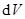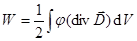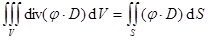И тогда для всего пространства 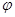пропорционален 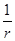, 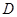пропорционален 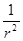, 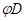пропорционально , т.е. последний интеграл для всего пространства ( 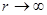) равен нулю. Т.е.

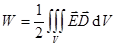, откуда энергия единицы объема

.

Рассуждая похожим образом, находим плотность энергии магнитного поля:

.

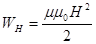Для магнитного поля еще рассматривается энергия магнитного контура с током. При увеличении силы тока источник отдает энергию на создание магнитного поля. Это есть работа на увеличение 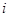от 0 до .

,

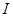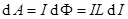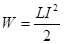- собственная энергия тока.