Определение оптимального (равновесного) объема производства фирмы путем сопоставления предельного дохода с предельными, средними валовыми и средними переменными издержками.

Второй способ определения оптимального (равновесного) объема производства основан на сравнении цены единицы продукции со средними валовыми и средними переменными издержками фирмы.

Чтобы сравнить их графически, построим кривые средних валовых издержек АТС, средних переменных издержек AVC, а также график предельного дохода или равновесной цены MR.

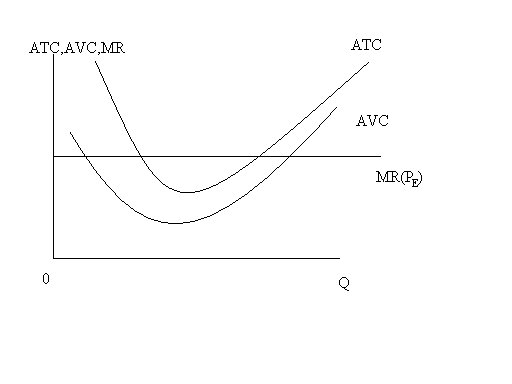
Рисунок 9.6. Кривые средних валовых издержек, средних переменных издержек и предельного дохода.

Чтобы определить средние издержки для оптимального или равновесного объема производства, вначале необходимо найти состояние равновесия фирмы, то есть точку пересечения MRи MC.

Рассмотрим случай, когда фирма работает с прибылью. Это возможно, если Р>АТС.

MR,MC,ATC

PE

L′

QE

Q

MR(PE)

ATC

E

MC

L

Рисунок 9.7. Определение оптимального (равновесного) объема производства фирмы.

Условие равновесия фирмы соблюдается в точке Е при объеме производства Q_Е. Именно этот объем является оптимальным (равновесным) и максимизирующим прибыль.

Определим графически средние валовые издержки фирмы АТС при объеме продукции Q_Е. Для этого найдем расстояние от точки Q_Е до графика АТС. Оно соответствует отрезку Q_EL.

Цена единицы продукции графически выражается отрезком Q_ЕЕ.

Чтобы определить среднюю прибыль с единицы продукции, надо из ее цены вычесть средние валовые издержки, т.е. найти разность (P_E– АТС). На графике она соответствует разности отрезков (Q_EЕ - Q_EL), или отрезку LЕ.

Общая прибыль фирмы равна произведению средней прибыли с единицы продукции на объем произведенной продукции, т.е. (Р_Е - АТС) х Q_Е.

Графически она изображается площадью прямоугольника P_EELL′.

При правильном построении площадь этого прямоугольника должна совпадать с площадью «петли» между кривой МС и графиком предельного дохода MR, так как обе площади показывают общую прибыль фирмы, выраженную различными способами.

S_петли АКЕ = S_•P_EELL^′

Перейдем теперь к рассмотрению ситуации с убытками.

Фирма несет убытки, если цена единицы продукции ниже средних валовых издержек, т.е. Р<АТС.

Если цена единицы продукции меньше средних валовых издержек, но больше средних переменных издержек, то для минимизации убытков фирма должна продолжить выпуск продукции. Этому условию отвечает неравенство АVC<Р<АТС.

Рассмотрим пример.

Р = 81$

AFC = 16$

AVC = 75$

Q = 100

Определим, как должна вести себя фирма при таких значениях издержек.

ATC = AFC + AVC = 91$

Следовательно, соблюдается неравенство:

АVC<Р<АТС

75$<81$<91$

При продолжении работы фирма полностью возместит непосредственные затраты на выпуск единицы продукции, т.е. средние переменные издержки AVC. После этого у нее с каждой единицы продукции останется (Р –AVC) = (81 – 75) = 6($). Фирме придется доплачивать на возмещение средних постоянных издержек AFC сумму (16 – 6) = 10 ($). Это средние убытки фирмы с каждой единицы продукции.

Общие убытки фирмы составят 10 х 100 = 1000 ($).

Если фирма прекратит производство, то ее общие убытки составят AFC х Q = 16 х 100 = 1600 ($). Таким образом, фирме выгоднее продолжать работать.

Покажем это графически:

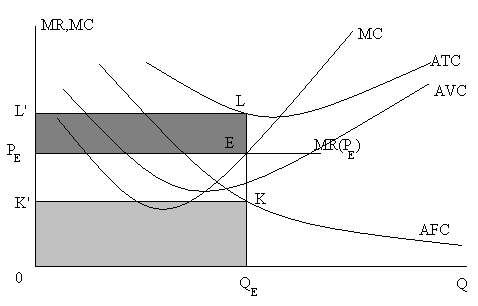
Рисунок 9.8. Фирма продолжает работать для минимизации убытков.

Равновесный объем производства фирмы определяется на основе условия равновесия фирмы MR = MC. Точка Е - это точка равновесия фирмы. Равновесный объем равен Q_Е. При таком объеме производства средние валовые издержки фирмы равны отрезку Q_EL ( расстояние от точки Q_Е до кривой АТС). Средний убыток на единицу продукции равен (АТС – Р). На графике это отрезок EL.

Общие убытки фирмы равны (АТС - Р) х Q_Е. Графически они соответствуют площади прямоугольника ELL′P_E.

В случае прекращения работы фирма понесла бы общие убытки, равные постоянным издержкам FC. Поскольку FC = AFC х Q_E, то на графике это площадь прямоугольника OK′KQ_E.

Если убытки фирмы таковы, что цена единицы продукции не покрывает даже непосредственных затрат на выпуск этой единицы, т.е. средних переменных издержек, то для минимизации убытков фирма должна прекратить производство. В этом случае Р<AVC.

Проиллюстрируем это примером.

Р = 71$

АFC = 16$

AVC = 75$

Q = 100

При продолжении работы фирма с каждой единицы продукции несет убыток (AVC – P) или (75 – 71) = 4($). Общий убыток с единицы продукции составляет (4 + 16) = 20($). Суммарный убыток фирмы со ста единиц продукции равен (20 х 100) = 2000($).

При прекращении производства убыток фирмы равен постоянным издержкам FC, которые составляют AFC х Q_E = 16 х 100 = 1600($).

Следовательно, выгоднее прекратить производство.

Изобразим этот случай графически.

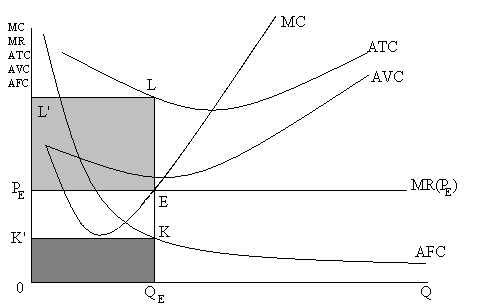
Рисунок 9.9. Фирма прекращает производство для минимизации убытков.

Так как Р<AVC, то кривая AVC на всем протяжении находится выше MR (P_Е). Пересечение графиков MR и МС дают точку равновесия Е, однако для минимизации убытков фирма не должна выпускать равновесный объем производства Q_E. Если она его выпустит, то ее средние валовые издержки составят отрезок Q_EL, а средние убытки на единицу продукции будут равны отрезку EL.

Общие убытки фирмы - площадь прямоугольника L′LEP_E.

Если фирма прекращает работу, то она обеспечивает минимальные убытки. Это площадь прямоугольника K′KQ_EO.

Обобщим рассмотренные закономерности.

Таблица 9.1