Угловой коэффициент или коэффициент наклона прямой измеряется как отношение изменения ординаты к изменению абсциссы на определенном интервале графика.
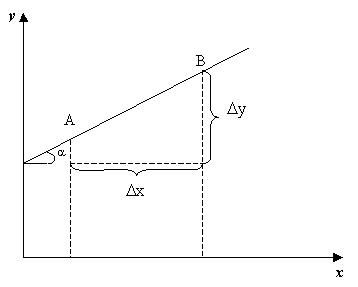
Рисунок 7.3. Угловой коэффициент графика линейной функции.
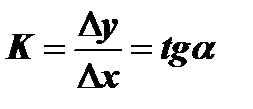 , где (7.3)
, где (7.3)
K- угловой коэффициент;
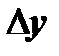 – изменение ординаты;
– изменение ординаты;
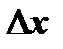 – изменение абсциссы.
– изменение абсциссы.
2. Положительным называют угловой коэффициент графика, если при увеличении абсциссы увеличивается и ордината. Такой угловой коэффициент имеют графики возрастающих функций.
Отрицательным называют угловой коэффициент графика, если при увеличении абсциссы ордината уменьшается.
Угловые коэффициенты графиков линейных функций во всех точках постоянны.
К1 = К2 = К3 = ...Кn = tg a
Угловые коэффициенты графиков нелинейных функций или кривых в разных точках различны и определяются угловыми коэффициентами касательных к кривым в этих точках.
Построим кривую, проходящую через следующие точки:
А (2;3); В (4;5); С (8;7); Д (13;5); Е (15;3).
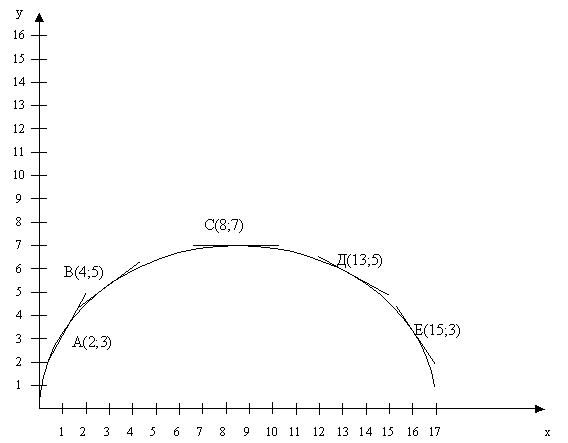
Рисунок 7.4. Угловые коэффициенты графика нелинейной функции.
Абсолютные величины угловых коэффициентов выпуклых кривых уменьшаются при движении вправо вниз вдоль этих кривых, а абсолютные величины угловых коэффициентов вогнутых кривых увеличиваются при движении вправо вниз.
Проиллюстрируем это на конкретном примере. Построим кривую, проходящую через точки А (2;5); В (3;3); С (6;1).
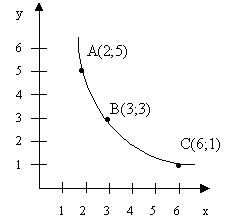
Рисунок 7.5. График выпуклой кривой.
В экономической теории, в отличие от математики, где кривые такого вида считаются вогнутыми, они признаются выпуклыми.
Определим угловые коэффициенты этого графика на интервалах АВ и ВС.
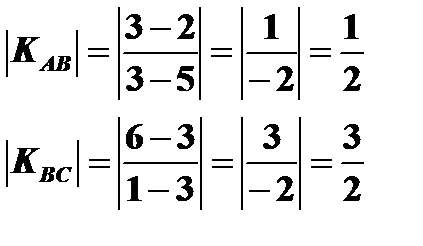
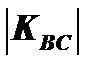 <
< 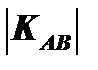
Следовательно, угловые коэффициенты выпуклой кривой уменьшаются при движении вправо вниз вдоль кривой.
Построим теперь кривую, проходящую через точки А (7;7); В (9;5); С (10;3).
Она окажется вогнутой.
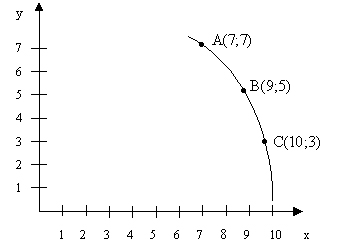
Рисунок 7.6. График вогнутой кривой.
Определим угловые коэффициенты этой кривой на интервалах АВ и ВС.
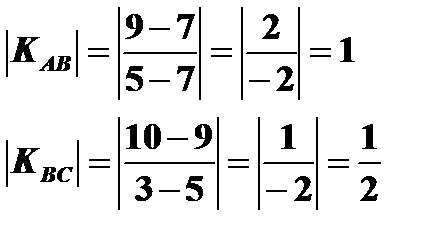

5. Бюджетная линия. Кривые безразличия и их свойства.
Потребительское поведение можно описать с помощью бюджетной линии и кривых безразличия.
Бюджетная линия - это графическое изображение всех возможных комбинаций количеств двух продуктов, которые доступны потребителю при данной величине его бюджета.
Пример. Потребитель имеет доход 12 долларов и покупает продукты А (сыр) и В (мясо). Цена единицы продукта А равна 1,5 доллара (PА = 1,5 долл.). Цена единицы продукта В равна 1 доллару (PВ = 1долл.). Покажем возможные комбинации продуктов А и В.
Таблица 7.4
Бюджет потребителя, выраженный через комбинации продуктов А и В.
| QА (Количество продукта А), ед. | QВ (Количество продукта В), ед. | Бюджет или суммарные расходы, в долларах |
| 8 x 1,5 = 12 | ||
| 6 x 1,5 + 3 x 1 = 12 | ||
| 4 x 1,5 + 6 x 1 = 12 | ||
| 2 x 1,5 + 9 x 1 = 12 | ||
| 1 x 12 = 12 |
Построим на основе этих данных бюджетную линию.
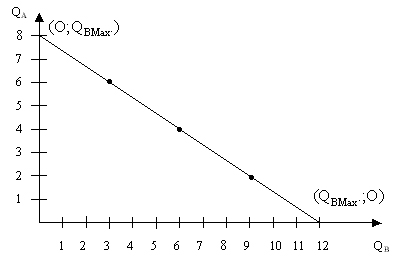
Рисунок 7.7. Бюджетная линия.
При построении бюджетных линий и кривых безразличия вертикальную ось принято обозначать QА, а горизонтальную - QВ.
Бюджетная линия имеет отрицательный угловой коэффициент, т.к. выражает убывающую функцию.
Рассмотрим свойства бюджетной линии:
1. Абсолютная величина углового коэффициента бюджетной линии равна отношению максимального количества продукта А к максимальному количеству продукта В или отношению цены продукта В к цене продукта А, т.е. :
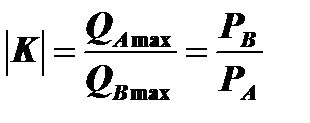 , где (7.4)
, где (7.4)
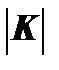 – абсолютная величина углового коэффициента бюджетной линии;
– абсолютная величина углового коэффициента бюджетной линии;
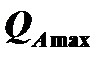 – максимальное количество продукта А;
– максимальное количество продукта А;
 – максимальное количество продукта В;
– максимальное количество продукта В;
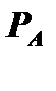 – цена продукта А;
– цена продукта А;
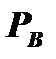 – цена продукта В.
– цена продукта В.
Докажем это свойство.

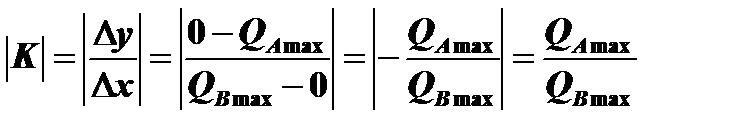

Выразим бюджет потребителя, исходя из условия, что сначала приобретается только продукт А, а затем только продукт В. В первом случае потребитель приобретет максимальное количество продукта А, а во втором случае – максимальное количество продукта В. Бюджет составит:
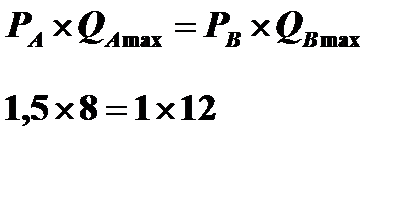
С учетом свойства пропорции получим:
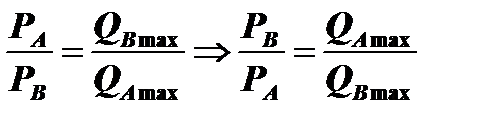
Следовательно,
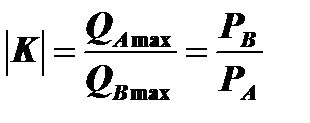
2. Изменение бюджета или дохода потребителя приводит к смещению бюджетной линии:
· Если бюджет увеличивается, то бюджетная линия смещается вправо, т.к. возрастает максимальное количество обоих продуктов.
· Если бюджет уменьшается, то бюджетная линия смещается влево.
3. Изменение цен продуктов А и В смещает крайние точки бюджетной линии:
· Если цена продукта А увеличивается, то верхняя точка бюджетной линии смещается вниз.
· Если цена продукта А уменьшается, то верхняя точка бюджетной линии смещается вверх.
· При увеличении цены продукта В нижняя точка бюджетной линии смещается влево.
· При понижении цены В нижняя точка бюджетной линии смещается вправо.
 Одновременное повышение цен продуктов А и В сдвигает бюджетную линию влево; одновременное снижение цен продуктов А и В смещает бюджетную линию вправо.
Одновременное повышение цен продуктов А и В сдвигает бюджетную линию влево; одновременное снижение цен продуктов А и В смещает бюджетную линию вправо.
Рассмотрим теперь кривую безразличия.
Кривая безразличия- это графическое изображение всех возможных комбинаций количеств продуктов А и В, которые обеспечивают потребителю одинаковую совокупную полезность или одинаковое удовлетворение потребностей.
Кривую безразличия впервые построил представитель кембриджской или английской школы неоклассического направления Фрэнсис Исидро Эджуорт.
Для построения кривой безразличия рассмотрим следующие условные данные. Представим, что для удовлетворения потребностей человека в пищевых продуктах равнозначны следующие комбинации продуктов А и В, например, мяса и сыра.
Таблица 7.5
Таблица безразличия (комбинации продуктов А и В, равноценные для потребителя по совокупной полезности).
| Комбинации | QА | QВ |
| С | ||
| Д | ||
| Е | ||
| F |
В приведенной таблице, которую принято называть таблицей безразличия, приведены равноценные для потребителя, с точки зрения их совокупной полезности, комбинации продуктов А и В. В этом смысле потребителю безразлично, какую комбинацию выбрать.
Построим на основе этих данных кривую безразличия.
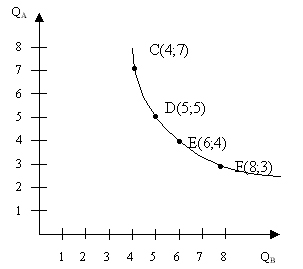
Рисунок 7.8. Кривая безразличия.
Кривые безразличия характеризуют субъективные предпочтения потребителей, т.к. для разных потребителей один и тот же продукт может обладать различной полезностью в силу индивидуальных отличий во вкусах и потребностях людей.
Кривые безразличия принято обозначать буквами I или IC от английского “indifference curve” (кривая безразличия).
Еще раз подчеркнем, что совокупная полезность каждой пары продуктов, соответствующей точкам С, Д, Е, F, одинакова.
Рассмотримсвойства кривых безразличия.
1. Кривые безразличия имеют отрицательный угловой коэффициент. Это значит, что любая кривая безразличия на всем протяжении убывает.
Докажем это методом от противного.
Представим, что кривая безразличия на определенном интервале возрастает.
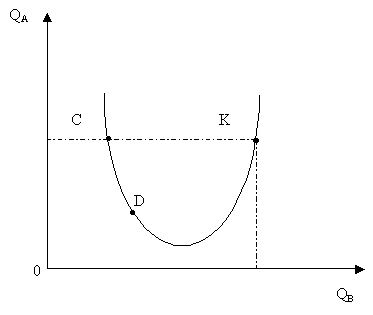
Рисунок 7.9. Кривая безразличия возрастает на интервале ДК (доказательство методом от противного).
Это значит, что на возрастающем интервале можно найти некоторую точку К, в которой количество продуктов А и В больше, чем на убывающем интервале. Следовательно, набор продуктов К предпочтительнее для потребителя, чем наборы С и Д, т.к. он обладает большей совокупной полезностью. Однако это противоречит определению кривой безразличия. Значит, исходное предположение было неверным.
2. Абсолютная величина углового коэффициента безразличия в любой точке кривой безразличия равна отношению предельной полезности продукта В к предельной полезности продукта А или предельной норме замещения. Предельная норма замещения - это пропорция, в которой продукт В замещает продукт А. Она показывает, сколько единиц продукта А замещает одна единица продукта В.
Предельная норма замещения обозначается MRS – от английского названия этого термина (marginal rate of substitution).

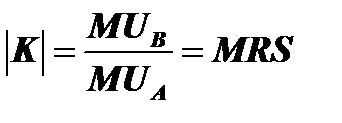 , где (7.5)
, где (7.5)
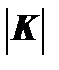 – абсолютная величина углового коэффициента безразличия;
– абсолютная величина углового коэффициента безразличия;
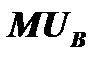 – предельная полезность продукта В;
– предельная полезность продукта В;
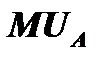 – предельная полезность продукта А;
– предельная полезность продукта А;
 – предельная норма замещения.
– предельная норма замещения.
Подтвердим справедливость этого соотношения для интервала СД кривой безразличия.
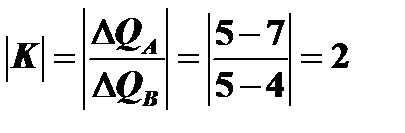
Определим предельную норму замещения на этом же интервале. При переходе от комбинации С к комбинации Д потребитель теряет 2 единицы продукта А и получает одну единицу продукта В. Это значит, что одна единица продукта В замещает 2 единицы продукта А. Значит,  = 2.
= 2.
Сравним предельные полезности продуктов А и В. Так как единица продукта В равноценна двум единицам продукта А, то предельная полезность продукта В в два раза выше предельной полезности продукта А. То есть, 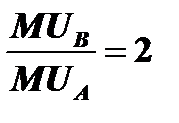 .
.
Следовательно, 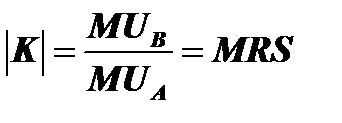 .
.
3. Кривые безразличия являются выпуклыми, поэтому абсолютная величина их углового коэффициента уменьшается по мере движения вниз вправо вдоль этих кривых.
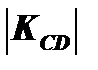 = 2
= 2


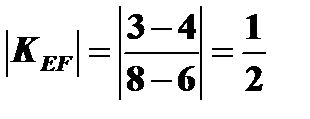
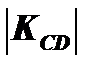 >
> 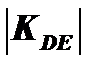 >
> 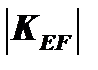
4. Через любую точку в системе координат QА и QВ можно построить кривую безразличия. Множество кривых безразличия называется картой безразличия. Чем выше расположена кривая безразличия, тем большую совокупную полезность благ она отражает.
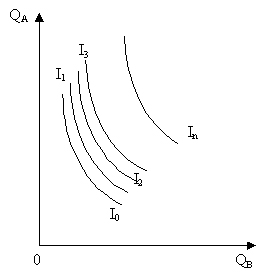
Рисунок 7.10. Карта безразличия.
5. Кривые безразличия не пересекаются.
Докажем это методом от противного Представим, что кривые безразличия I1 и I2 пересеклись.
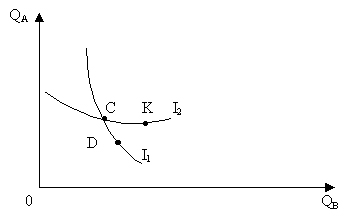
Рисунок 7.11. Пересечение кривых безразличия (метод от противного).
Наборы продуктов С и Д равноценны для потребителя, т.к. принадлежат одной и той же кривой безразличия I1. Наборы продуктов С и К тоже равнозначны, т.к. также принадлежат одной и той же кривой - I2. Однако, комбинация продуктов К предпочтительнее для потребителя, чем комбинация продуктов Д, т.к. точка К находится выше и правее, а поэтому содержит большее количество продуктов А и В.
С = Д, С = К, но К > Д , что противоречит логике.
Значит, исходное предположение было неверным. Следовательно, кривые безразличия не пересекаются.
Дата добавления: 2021-02-19; просмотров: 1052;











