ДВИЖЕНИИ ЖИДКОСТИ (ГАЗА)
При естественной конвекции движение возникаетпод действием разности плотностей нагретых и холодных масс неравномерно нагретого теплоносителя. Нагреваемые от стенки объемы теплоносителя становятся легче и под действием возникающей подъемной силы всплывают, а охлаждаемые опускаются. Таким образом, для возникновения свободного движения жидкости (газа) нобходима разность температур (температурный напор) между стенкой и теплоносителем..
Свободная конвекция имеет место у нагретых стен печей, топок котлоагрегатов, трубопроводов, у батарей центрального отопления, в холодильниках при охлаждении продуктов и др.
Различают процессы конвективного теплообмена, протекающие в большом по сравнению с размерами тела «неограниченном» простран-стве, и процессы теплообмена, протекающие в ограниченном простран-стве.
Рассмотрим свободный теплообмен в неограниченном пространстве. Характер движения теплоносителя около стенки зависит от формы поверхности, ее положения в пространстве и направления теплового потока. На рис. 3.12 показана картина движения теплоно-сителя около охлаждаемой вертикальной стенки или трубы (а), около охлаждаемых (б и в) и около нагреваемых горизонтальных поверхностей (г и д).
Движение теплоносителя вдоль охлаждаемой вертикальной стенки (трубы) в нижней части имеет ламинарный характер, выше – переход-ный, а затем – вихревой. В случае нагреваемой стенки теплоноситель перемещается сверху вниз, и характер течения изменяется в той же последовательности. Режим течения определяется главным образом температурным напором, с увеличением которого сокращается длина участка, занятого ламинарным потоком и увеличивается зона вихревого движения. На участке ламинарного движения коэффициент теплоотдачи уменьшается в соответствии с увеличением толщины ламинарного слоя теплоносителя. В зоне вихревого движения коэффициент теплоотдачи имеет практически одинаковое значение для всей поверхности.
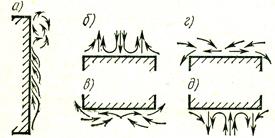
Рис. 3.12. Характер свободного движения теплоносителя в
неограниченном пространстве
Характер движения теплоносителя около плоских горизонтальных поверхностей зависит от их расположения и направления теплового потока. При картине движения, отвечающей схемам в и г на рис. 3.12, поверхность стесняет движение теплоносителя, и потому теплообмен протекает менее интенсивно, чем в случаях б и д на рис. 3.12.
На рис. 3.13 показан характер свободного движения теплоносителя около горячих горизонтальных труб различных диаметров. У труб малого диаметра восходящий поток сохраняет ламинарный режим даже вдали от трубы. При большом диаметре переход в турбулентный режим может происходить в пределах поверхности самой трубы.
Анализ многочисленных экспериментальных исследований теплоотдачи при свободном движении теплоносителя в неограниченном пространстве показал, что для средних коэффициентов теплоотдачи можно записать уравнение подобия, которое справедливо для различных форм поверхности теплообмена:
Nuж = С(Grж· Prж)nε. (3.63)
Значения С,n и ε приведены в таблице 3.6.
Физические свойства λ, ν, β и α в уравнении (3.63) выбираются по средней температуре теплоносителя.
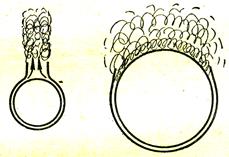
Рис. 3.13. Характер свободного движения теплоносителя около
горячих горизонтальных труб
.
Расчет теплоотдачи вертикальных труб и пластин при значениях Gr·Pr > 109 производится отдельно для начального участка высотой Нкр, занятого ламинарным пограничным слоем, и для участка Н – Нкр, занятого турбулентным течением. Значение Нкр определяется из условия
Gr·Pr = gβ∆ТНкр3/να = 109. (3.64)
Среднее по высоте значение коэффициента теплоотдачи
α = αлНкр/Н + αт(1 - Нкр/Н), (3.65)
где αл и αт - средние коэффициенты теплоотдачи на участках ламинарного и турбулентного пограничных слоев;
Н – полная высота пластины или длина трубы.
Характер свободного движения теплоносителя в ограниченном пространстве зависит от формы и взаимного расположения поверх-ностей, образующих прослойку, рода теплоносителя, температурных характеристик поверхностей, ограничивающих пространство, а также от расстояния между ними.
Движение теплоносителя по-разному протекает в замкнутых и открытых прослойках.
Таблица 3.6. Значения С, n и ε в уравнении (3.63)
| Условия теплоотдачи | C | n | ε | Опреде- ляющий размер |
| Вертикальная пластина и вертикальная труба: ламинарный пограничный слой Gr·Pr = 103 – 109 турбулентный пограничный слой Gr·Pr > 109 | 0,8 0,15 | 0,25 0,33 | 1+(1+ +1/√Pr)2] | Длина трубы, пластины |
| Горизонтальная труба: 10-3 ≤ Gr·Pr ≤ 103 103 ≤ Gr·Pr ≤ 108 | 0,18 0,5 | 0,13 0,25 | Диаметр трубы |
| Горизонтальная пластина, охлаждаемая сверху: ламинарный режим течения турбулентный режим течения | 0,54 0,14 | 0,25 0,33 | Короткая сторона пластины |
| Горизонтальная пластина, охлаждае- мая снизу, ламинарный режим | 0,27 | 0,25 |
Движение теплоносителя по-разному протекает в замкнутых и открытых прослойках.
На рис. 3.14 рассмотрены два случая теплоотдачи при свободном движении теплоносителя в ограниченном пространстве: теплоотдача в замкнутой прослойке (а) и теплоотдача в открытом зазоре при одинаковой температуре стенок, образующих зазор (б).
При теплоотдаче в замкнутом пространстве перенос теплоты осуществляется одним и тем же теплоносителем, который циркулирует между горячей и холодной стенками, образуя замкнутые контуры. В этом случае трудно отделить теплоотдачу около охлаждаемой и нагреваемой поверхности. Из-за сложности процессов определить коэффициент теплоотдачи обычным путем с учетом особенностей движения не удается. Поэтому процесс теплообмена в замкнутой про-
слойке оценивают в целом, определяя плотность теплового потока q формулой теплопроводности:
q = λэкв(Тст1 – Тст2) / δ, (3.66)
где λэкв – эквивалентный коэффициент теплопроводности, учитываю-
щий конвективный перенос теплоты;
Тст1 и Тст2 – температуры горячей и холодной поверхностей, разделен-
ных прослойкой;
δ – толщина прослойки.
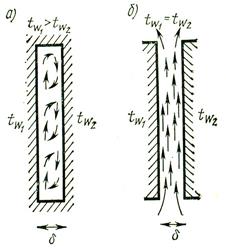
. 3.14. Характер свободного движения теплоносителя в
ограниченном пространстве
Эквивалентный коэффициент теплопроводности учитывает интенсивность циркуляции в прослойке и определяется через коэффи-циент теплопроводности теплоносителя по формуле:
λэкв = εкλ, (3.67),
где εк – поправочный коэффициент (коэффициент конвекции),
учитывающий влияние конвекции;
λ - коэффициент теплопроводности теплоносителя.
Опытное исследование теплоотдачи в замкнутом пространстве показало, что независимо от формы прослойки коэффициент конвекции можно определить из уравнения:
εк = с(Grж·Prж)n, (3.68)
в котором с и n зависят от величины произведения Grж·Prж.При Grж·Prж = = 103 – 106 значения с = 0,105 и n = 0,3, при Grж·Prж = 106 – 1010 с = 0,4 и n =0,2. При Grж·Prж ≤ 103 εк = 1, т.е. циркуляция отсутствует, и теплота передается только теплопроводностью. Конвекция отсутствует также в горизонтальных щелях, если нагретая поверхность расположена сверху.
В уравнении (3.68) за определяющую выбрана средняя температура теплоносителя, равная полусумме температур стенок, а за определя-ющий размер – толщина прослойки δ.
При теплоотдаче в открытом зазоре при свободном движении теп-лоносителя между вертикальными стенками, имеющими одинаковую температуру, существует критическая величина зазора, при которой теплообмен достигает наибольшей интенсивности. При зазорах меньше критического интенсивность теплообмена резко ухудшаеся, а при зазорах больше критического – остается практически неизменной. При теплоотдаче в воздухе критическая величина зазора определяется из равенства
Grжδ/2h ≈ 20, (3.66)
где δ – расстояние между стенками;
h - высота стенки.
При подсчете числа Gr за определяющий размер принята половина расстояния между стенками.
Теплоотдача в зазоре протекает более интенсивно, чем при свободном движении около одиночной пластины. При расстояниях между вертикальными стенками, близких к критическим (Grжδ/2h = 10 – 100), опытные данные по теплоотдаче удовлетворительно описываются уравнением:
Nuж = 0,65(Grж· Prж δ/2h)0,25. (3.67)
Определяющий размер здесь выбирается так же, как в уравнении (3.66).
Контрольные вопросы
1. Опишите картину свободного движения теплоносителя в неог-
раниченном пространстве
2. Какое уравнение подобия применяют при свободном движении теплоносителя в неограниченном пространстве?
3. По какой формуле определяют среднее по высоте значение коэффициента теплоотдачи вертикальных труб и пластин при свободном движении теплоносителя?
4. Опишите картину свободного движения теплоносителя в огра-ниченном пространстве.
5. По какой формуле оценивают в целом процесс теплообмена в замкнутой прослойке?
6. Как определяется эквивалентный коэффициент теплопровод-ности в замкнутой прослойке?
7. Что означает и как определяется критическая величина открытого зазора при свободном движении теплоносителя между вертикальными стенками?
8. Какое уравнение подобия применяют при теплоотдаче в открытом зазоре при свободном движении теплоносителя меж-ду вертикальными стенками?
Дата добавления: 2021-02-19; просмотров: 542;











