Теория кристаллического поля, модель Людвига-Вудбери для d-ионов в алмазоподобных кристаллах

Для ионов переходных элементов (с неполностью заполненными d-, f-оболочками оболочками) в полупроводниках и диэлектриках характерно малое отличие в волновых функциях d- или f- состояний в кристалле от таковых для свободных ионов. При этом энергетические уровни d- или f- состояний оказываются глубоко внутри запрещённой зоны кристалла, а волновые функции оказываются слабо возмущёнными действующим на них кристаллическим окружением. Это объясняется сильной локализацией электронной плотности d- и f-состояний, часто в пределах первой и второй координационных сфер. Наиболее простой вариант теории кристаллического поля (ТКП) для описания возмущения таких состояний кристаллов сводится к действию на электроны такого ПЦ статического электрического поля точечных зарядов ионов кристалла

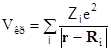, (1.2.31)

где Z_i и R_i - заряд и координата i-го, соседнего ионов кристалла. Причём характер расщепления определяется расстоянием и симметрией расположения, в основном, ближайших соседних атомов из первой, второй координационных сфер. Матричные элементы возмущения (1.2.31) на волновых функциях j_m d- (f-) - состояний

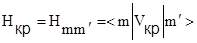(1.2.32)

определяют вклад кристаллического поля в спиновый гамильтониан (1.2.12) или его более сложную форму с учётом слагаемых более высокого порядка, например (1.2.13). Вместе с тем, расчёт расщеплённых кристаллическим полем энергетических уровней позволяет предсказать возможные значения магнитного момента ПЦ. В первом порядке теории возмущений энергетические уровни определяются диагонализацией матрицы

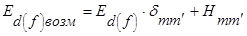, (1.2.33)

где - Е_d(f) - энергия невозмущенных d- или f-состояний иона.

Расчёты по формуле (1.2.33) не сложны, но громоздки. Примеры таких расчётов есть, например, в книге [7]. Но часто характер расщепления можно качественно предвидеть, исходя из симметрии d- или f- волновых функций и симметрии кристаллического поля. Рассмотрим, как это происходит на примере 3d- состояний ионов элементов группы железа в поле с кубической симметрией.

Без учёта спин-орбитального взаимодействия состояние одного d-электрона (2l+1)=5- кратно вырождено, где l=2 - максимальная проекция орбитального момента d-электрона (в единицах магнетона Бора).

Волновые функции d-состояний можно представить в действительной форме

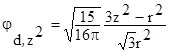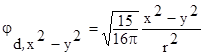; ; (1.2.34)

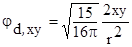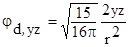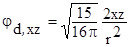; ; . (1.2.35)

Форма всех пяти орбиталей показана на рис.1.2.4. Они разбиваются на две группы, которые часто обозначают е- и t₂-состояния.

Два верхних x²-y² и z², е-состояния на рис.1.2.4 имеют максимумы электронной плотности вдоль осей декартовой системы координат. Три других t₂-состояния, внизу, на рис.1.2.4, имеют максимумы электронной плотности в направлениях в плоскости (x,y) между осями x и y для j_d,xy , в плоскости (x,z) между осями x и z для j_d,xz и в плоскости (y,z) между осями y и z для j_d,yz .

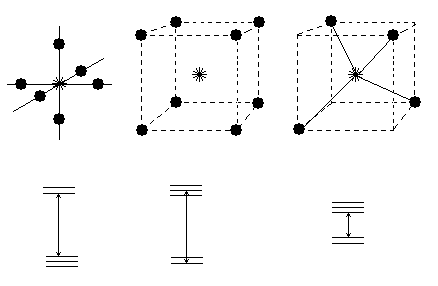
В простом варианте ТКП соседние ионы заменяются отрицательными точечными зарядами. Это связано с тем, что на d-состояния большее влияние оказывают электронные оболочки соседних атомов, а не их ядра. В кубическом кристалле или молекуле с кубической симметрией ближайшие соседи 3d-иона могут располагаться в вершинах октаэдра, куба или тетраэдра, как на рис. 1.2.5.

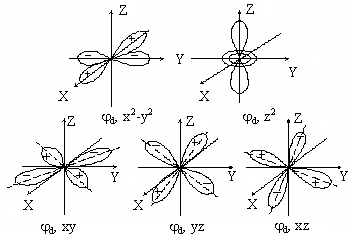Рис.1.2.4. Форма угловых частей d-орбиталей свободного иона.

Сопоставляя форму d-орбиталей на рис.1.2.4 с положением отрицательных точечных зарядов соседей 3d- иона на рис.1.2.5, можно видеть, что наиболее сильно в октаэдрическом поле будут отталкиваться от этих зарядов, и, следовательно, повышать свою энергию, электроны на t₂-орбиталях, у которых максимумы электронной плотности как раз направлены на эти точечные заряды. Состояния е с максимумами между осями x, y и z повышают свою энергию в меньшей степени. Поэтому пятикратно вырожденный d-уровень

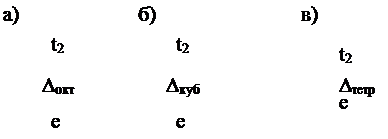
Рис. 1.2.5. Расщепление d- состояний в поле точечных зарядов:

а)- октаэдрическом, б)- кубическом и в)- тетраэдрическом.

Значком * показано местоположение 3d- иона.

расщепляется на t₂-триплет и е-дублет, как на рис.1.2.5, с параметром кристаллического октаэдрического поля D_окт . В случае кубического и тетраэдрического полей аналогичные рассуждения дают обратный порядок следования уровней. Причём

D_тетр»0,5D_куб»-0,5D_окт . (1.2.36)

Для 3d-ионов в алмазоподобных полупроводниках для классификации возможных состояний этих ионов Людвигом и Вудбери [3] была предложена эмпирическая модель, основанная на анализе множества исследований ЭПР 3d-ионов в кремнии и соединениях A³B⁵ , A²B⁶ . Суть её в следующем.

В случае ионов замещения электроны 4s- оболочки и недостающая часть электронов из 3d-оболочки идут на образование ковалентных связей. Оставшиеся электроны заполняют 3d-состояния, расщеплённые тетраэдрическим кристаллическим полем, по правилу Хунда.

В случае ионов внедрения электроны 4s- оболочки добавляются к тем, что были в 3d- оболочке. Состояния 3d-оболочки расщепляются как в октаэдрическом поле и заполняются также по правилу Хунда.

Тетраэдрическое расщепление для ионов замещения, так как в алмазоподобном полупроводнике в любом узле ближайшие соседи иона находятся в вершинах тетраэдра. Несколько сложнее дело в случае ионов внедрения. Для них также ближайшие соседи находятся в вершинах тетраэдра. Но шесть атомов следующей координационной сферы не намного, всего лишь в 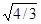≈ 1.15 раз дальше. Так как, согласно (1.2.36), октаэдрическое поле в два раза сильнее тетраэдрического, результирующий характер расщепления определяется второй координационной сферой, т.е. является октаэдрическим.

Рассмотрим два примера для примесного атома железа, у которого в свободном состоянии, как известно, имеет место следующее электронное заполнение оболочек: 1s²2s²2p⁶3s²3p⁶3d⁶4s² . Важны две последние валентные оболочки 3d⁶4s² , заполнение которых может меняться.

Первый пример - ион замещения в соединениях A³B⁵ (GaAs , GaP , InP и т.д.). Из опыта известно [3,6,9], что 3d- элементы преимущественно растворяются в кристалле в виде ионов замещения компоненты A с валентностью +3. Тогда 2 электрона из 4s- оболочки и один из 3d идут на образование ковалентных связей. Оставшиеся 5 электронов согласно правилу Хунда заполняют пять 3d-состояний с одинаковым направлением спина. Так как этим пяти состояниям соответствуют пять проекций орбитального момента от -2 до +2, суммарный орбитальный момент 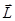равен нулю. Суммарный спин S=5/2. Таким образом, примесный ион замещения Fe³⁺ на месте галлия, то есть, Fe_S³⁺(Ga), имеет заполнение d-оболочки 3d⁵ и терм ⁶S.

Второй пример - примесный междоузельный атом железа в кремнии Fe_i . Опыт показывает, что 3d- примеси в кремнии занимают преимущественно положение внедрения. Для железа, согласно модели Людвига-Вудбери, два 4s-электрона окажутся в 3d-оболочке с заполнением 3d⁸ . Пять электронов будут иметь спин “вверх”, три других - “вниз”, то есть, S=1 . Причём, согласно схеме расщепления уровней на рис. 1.2.5а, три электрона не могут изменить своё орбитальное состояние, то есть, в отличие от свободного 3d⁸- иона с DL¹0 у иона в кристалле DL=0. Таким образом, имеем терм синглета 3A вместо ³F свободного иона. В таких случаях говорят, что орбитальный момент “заморожен” кристаллическим полем. Если ион железа потеряет один электрон, то есть, будет 3d⁷ , то согласно рис. 1.2.5а будет 3-х кратное орбитальное вырождение DL¹0, S=3/2 и вместо ⁴F свободного иона будет терм триплета ⁴T.