Тема 6. Растяжение и сжатие.
Механические характеристики материалов
 6.1. Напряжение и деформации при растяжении и сжатии.
6.1. Напряжение и деформации при растяжении и сжатии.
Закон Гука
Растяжение или сжатие стержня вызывается силами, действующими вдоль его оси. В этом случае в поперечных сечениях стержня возникает только продольная (нормальная) сила N и нормальные напряжения 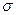 .
.
Так как поперечных сил нет, поэтому касательные напряжения в каждой точке поперечного сечения равны 0.
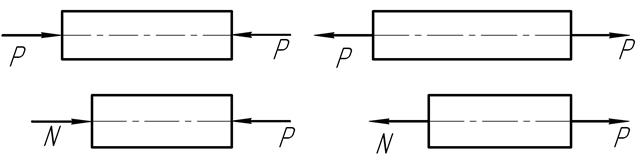
Закон распределения нормальных напряжений по поперечному сечению бруса устанавливается на основании гипотезы плоских сечений (гипотезы Я. Бернулли): сечения бруса, плоские и нормальные к его оси до деформации, остаются плоскими и нормальными к оси и при деформации.
Значит, при растяжении-сжатии бруса нормальные напряжения равномерно распределены по его поперечному сечению.
 N=
N= 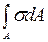 .
.
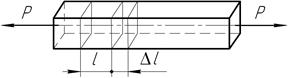
На основании гипотезы Бернулли следует заключить, что все волокна элемента длиной l удлиняются на ∆l и их относительные удлинения одинаковы:
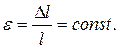
Закон Гука выражает линейную зависимость деформаций от напряжений:
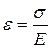 , или
, или 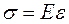 ,
,
где Е - коэффициент пропорциональности, называемый модулем упругости первого рода или модулем Юнга, МПа.
Учитывая, что E=const и 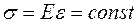 ,
,
Находим 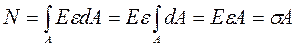 , отсюда
, отсюда
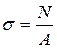 .
.
Определяя напряжения, в сопротивлении материалов пользуются принципом Сен-Венана:
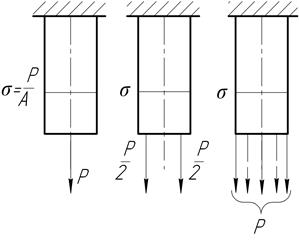
распределение напряжений существенно зависит от способа приложения внешних сил лишь вблизи места нагружения. В частях, достаточно удаленных от места приложения сил, распределение напряжений практически зависит только от статического эквивалента этих сил, а не от способа их приложения.
Закон Гука для относительной продольной деформации
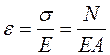 .
.
Закон Гука для абсолютной продольной деформации:
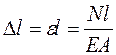 .
.
Здесь ЕА - жесткость поперечного сечения стержня при растяжении-сжатии.
c= 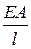 - жесткость стержня при растяжении-сжатии.
- жесткость стержня при растяжении-сжатии.
Если продольная сила и поперечное сечение стержня по длине не постоянны, то
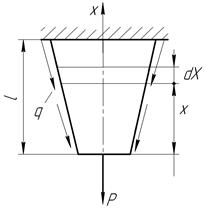
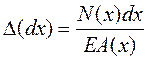 ;
;  .
.
Растяжение и сжатие сопровождаются также изменением поперечных размеров стержня.
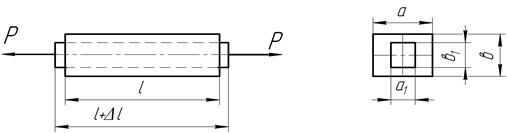
Абсолютные поперечные деформации:
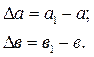
Относительные поперечные деформации:
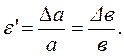
При растяжении поперечные деформации отрицательны, а при сжатии – положительны.
Коэффициент Пуассона:
μ=  .
.
μ - безразмерная величина, μ =0…0,5. Например, для каучука μ≈0,5, для стали μ≈0,3.
Коэффициент Пуассона μ и модуль упругости Е характеризуют упругие свойства материала.
Учитывая, что 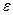 и
и 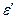 всегда имеют противоположные знаки, получим
всегда имеют противоположные знаки, получим
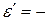 μ
μ 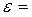 -μ
-μ 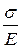 .
.
Дата добавления: 2016-11-29; просмотров: 1947;











