Нормирование уровня длинных импульсных помех с помощью схемы РОС

Схема РОС (расширяющий фильтр — ограничитель — сжимающий фильтр) работает по принципу: расширение сигнала Р — ограничение О — сжатие сигнала С и представляет собой последовательное соединение двух дисперсионных линий задержки ДЛЗ с сопряженными (т. е. различающи­мися знаками) фазо-частотными характеристиками и ограничителем между ними (рис.4.150).

Полосы пропускания ДЛЗ DF₁ выбираются равными шири­не спектра полезного сигнала (на уровне 2/p): DF₁ = П= 1/t₁ а длительность Т_р импульсной характеристики значительно больше длительности сигнала, т. е. Т_р>>t_1.

Сигнал, действуя на первую ДЛЗ, расширяется по длительности до Т_р и приобретает ЛЧМ с девиацией DF = П. Он становится сложным, ибо произведе­ние его ширины спектра на длительность

D_p = ПТ_p = T_p/t₁»l,

где D_p—коэффициент растяжения сигнала в ДЛЗ. После прохождения ограничителя он, будучи сложным, сжимается во второй ДЛЗ до прежней дли­тельности 1/DF = t₁, а его амплитуда увеличивается в 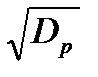раза по сравнению с амплитудой на выходе ограничителя, которая совпадает с амплитудой окру­жающего шума. Поэтому отношение сигнал-шум

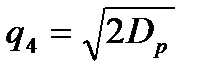
Прохождение помехи через рассматриваемую систему существенно зави­сит от ее длительности t₁. Ее спектр на уровне 2/p имеет ширину П₁ = 1/ t₁ (см. рис. 4.151,а). 'Гак как полоса пропускания ДЛЗ составляет лишь DF₁= 1/t₁, то ширина П₂ спектра короткой помехи на ее выходе ограничивается этой величи­ной (см. рис. 4.151,б):

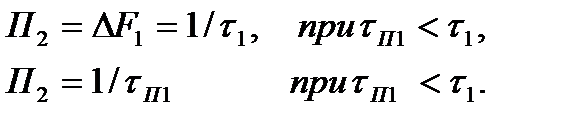
При 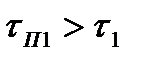, весь спектр помехи (на уровне 2/p) попадает в полосу про­пускания ДЛЗ, которая вследствие своей дисперсионности задерживает различ­ные гармонические составляющие на разное время, определяемое дисперсион­ной характеристикой этой ДЛЗ. Время задержки наиболее сильно различается па крайних (максимальной и минимальной) частотах спектра помехи. Разность этих временных задержек определяет длительность импульса помехи t_П2 на вы­ходе, которая, как это следует из подобия треугольников аbс и deg на диспер­сионной характеристике ДЛЗ (рис.4.150), составляет

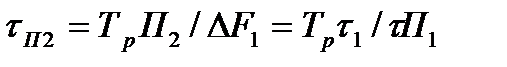
и уменьшается с увеличением t_П1 (рис.4.151,в). Последнее физически объ­ясняется сужением спектра помехи. Но длительность импульса на выходе растягивающего фильтра не может быть меньше длительности импульса на входе: t_П2 ³t_П1.

Минимальную величину t_П2 min = t_m определим из условия t_П2 = t_П1, из которого следует

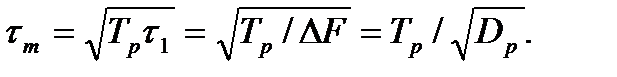
При действии более длительной помехи (t_П2 > t_П1) последняя не меняет своей длительности.

Итак, величина t_m является минимально возможной длительностью импульсной помехи на выходе ДЛЗ. Кроме того, она представляет собой длительность основного переходного процесса на выходе ДЛЗ (т. е. оптимального фильтра для ЛЧМ сигнала с длительностью Т_р и девиацией частоты DF₁), вызванного действием достаточно длинной немодулированной настроенной импульсной по­мехи.

Из предыдущего следует, что коэффициент сложности D₂ помехи на вы­ходе первой ДЛЗ, т. е. произведение ее ширины спектра П₂ на длительность t_П2, зависит от длительности помехи следующим образом (рис.4.151,г):

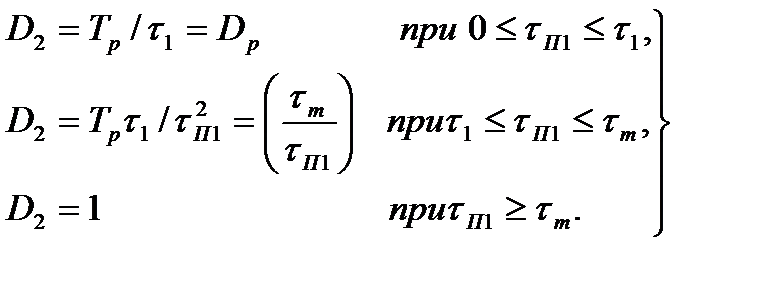. (4.72)

Поэтому после прохождения ограничителя, который сделает равными уровни помехи и шума, помеха во второй ДЛЗ при 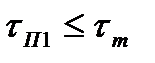сожмется, но дли­тельности в D₂ раз, увеличится по амплитуде в 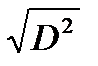раз и при этом в 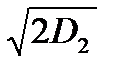раз превысит среднеквадратическое значение шума. При иной длительности поме­ха пройдет через ДЛЗ, не меняя амплитуды и длительности. Таким образом, от­ношение помеха-шум на выходе составляет (рис.4.151, д)

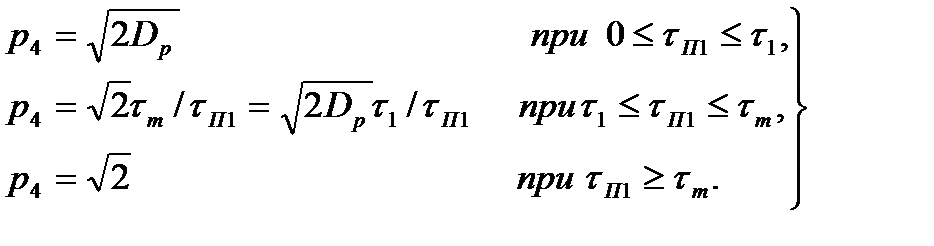. (4.73)

Следовательно, помехи, длительность которых превосходит 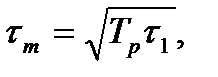, нормируются рассматриваемой схемой к уровню шума. Физически это объяс­няется тем, что столь длительные помехи, обладая сравнительно узким спек­тром, проходят через обе ДЛЗ, не подвергаясь растяжению и сжатию. Поэтому после ограничения они становятся на уровне шума. Таким образом, схема РОС осуществляет селекцию импульсных помех по ширине спектра.

Итак, если схема ШОУ нормирует уровень коротких импульсных помех, то схема РОС — уровень длинных импульсных помех. Возникает естественное стремление совместить достоинства обеих схем в единой системе обработки. Эта возможность и рассматривается ниже.