Скалярные признаки подклассов целей
Согласно теории разд. 2.2.4 для каждого подкласса целей, несмотря на многомерный характер дискретизированного портрета, таких признаков два.
Первый - это корреляционная сумма портрета с отсчетами 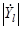 и ожидаемого нормированного портрета-эталона с отсчетами
и ожидаемого нормированного портрета-эталона с отсчетами 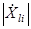 для i-го подкласса при условии
для i-го подкласса при условии 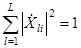 . Здесь
. Здесь  и
и 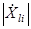 - модули комплексных чисел.
- модули комплексных чисел.
Корреляционная сумма имеет вид
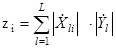 (1.8)
(1.8)
Она характеризует степень сходства принятого портрета с эталонными для различных подклассов.
Вторым признаком является энергетический параметр 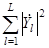 . Однократное его измерение или же результат усреднения по N реализациям можно использовать для вычисления в качестве признака эффективной площади цели по формуле (1.2). Эффективная площадь цели сводится при этом к сумме эффективных площадей разрешаемых по дальности элементов цели.
. Однократное его измерение или же результат усреднения по N реализациям можно использовать для вычисления в качестве признака эффективной площади цели по формуле (1.2). Эффективная площадь цели сводится при этом к сумме эффективных площадей разрешаемых по дальности элементов цели.
Диапазон флюктуаций σц при широкополосном однократном зондировании сужается по сравнению с узкополосным зондированием из-за дополнительного дальностного усреднения. Это подтверждается сравнением оценочных плотностей вероятности распределения Р(σц) для целей крупных (рис. 1.14,а), средних (ряс. 1.14,6) и малых (рис. 1.14,в) размеров (сплошные линии) в сравнении с приводившимися для узкополосных сигналов (штриховые линии). В связи с имеющим уже место усреднением в однократном зондировании требуется меньшее, чем при узкополосном облучении, число обращений к цели N. Это следует также из сопоставления зависимостей рис. 1.15 (сплошные линии) с аналогичными зависимостями рис. 7 для узкополосного сигнала (заштрихованная область на рис. 1.15). Показано, что уровень флюктуаций снижается в результате усреднения при широкополосном сигнале за меньшее число обращения к цели. Нормирование на рис. 1.15 проведено по отношению к уровню флюктуаций при узкополосном сигнале.
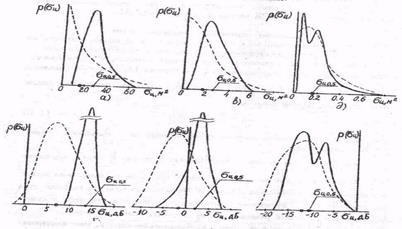
Рис. 1.14. Плотности распределения σцпри широкополосном (П=80 МГц, сплошные линии) и узкополосном (штриховые линии) зондировании, нормированного к своему максимальному значению при N=1 и узкополосном зондировании для крупноразмерных (1), среднеразмерных(2) и малоразмерных (3) целей соответственно
Дополнительным признаком может служить в ряде случаев радиальный размер цели. Он измеряется по некоторому уровню от максимума ДП либо по максимуму корреляционной суммы с эталонами прямоугольной формы различной протяженности. В ряде случаев удается пренебрегать даже зависимостью этого признака от признака "корреляционная"сумма для экспериментально полученных непрямоугольных эталонов. Это можно отвести за счет не учитываемого в теории "шума портретов" - их разброса относительно некоторого среднего портрета. Заметим, что "шум портретов" уменьшается при разбивке классов целей на подклассы - кластеры.
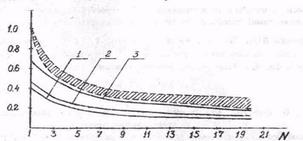
Рис. 1.15. Зависимости от числа усреднений N среднеквадратического отклонения ЭП при широкополосном (сплошные линии) и узкополосном (штриховые линии) зондировании, нормированного к своему максимальному значению при К=1 и узкополосном зондировании для крупноразмерных (I), среднеразмерных (2) и малоразмерных (3) целей соответственно
Дальностно-поляризационные портреты (ДПП)
Используя широкополосные (многочастотные) сигналы, можно получать поляризационную информацию не только о распознаваемых объектах в целом, но и об отдельных их элементах. Простейший ДПП - это совокупность двух ДП, полученных на ортогональных поляризациях, в частности, при однополяризационном зондировании. В натурном эксперименте подобные ДПП получались при последовательном одноканальном приеме на Украине в 1981 г.
Двухканальный прием имеет преимущества перед последовательным одноканальным. Он позволяет извлекать не только амплитудные, но и фазовые признаки, связанные с поляризационными особенностями элементов цели. В недавних работах [42, 128] проводилось распознавание макетов целей методом электродинамического моделирования по параметрам эллипсов поляризации для разрешаемых по дальности элементов целей. В качестве параметров эллипсов вводятся размеры ею главных осей и угол наклона большой оси.
С позиций согласованного двухканального приема и в пренебрежении "шумом портретов" скалярным признаком распознавания является корреляционная сумма ДПП [1, 138, 140].
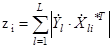 .
.
В ней, в отличиеот корреляционной суммы ДП, 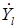 и
и 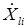 - векторные (двухэлементные) комплексные величины. Векторные величины
- векторные (двухэлементные) комплексные величины. Векторные величины 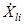 являются элементами ДПП. Эти элементы
являются элементами ДПП. Эти элементы 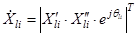 описываются парой вещественных характеристик приема
описываются парой вещественных характеристик приема 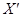 и
и 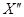 на ортогональных поляризациях и сдвигом фаз θli. Нормировка портрета означает, что
на ортогональных поляризациях и сдвигом фаз θli. Нормировка портрета означает, что
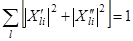 .
.
Дата добавления: 2021-02-19; просмотров: 631;











