Параллельное проецирование

Общие понятия метода проецирования

Операция проецирования является основой построения любого изображения.

Метод проекций заключается в проецировании каждой точки геометрического объекта на плоскость.

Рассмотрим точку А - геометрический объект. Зададим некоторую плоскость p - плоскость проекций и точку S, не принадлежащую p - центру проекций (рис. 1.1). Спроецируем точку А на плоскость p, проведем через точки S и А проецирующую прямую SA. Точка А_pпересечения Рис. 1.1.

проецирующей прямой SA с плоскостью p есть проекция точки А. Плоскость p и центр S – аппарат проецирования. В зависимости от выбора аппарата проецирования различают центральное и параллельное проецирование.

Центральное проецирование

Аппаратом центрального проецирования является плоскость проекции p и центр проецирования точка S, причем S не принадлежит p. Сущность способа в том, что все проецирующие лучи исходят из центра S.

Рассмотрим ряд произвольных точек и определим их центральные проекции (рис. 1.2).

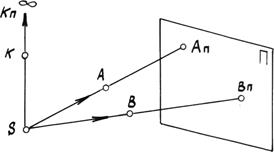
Рис. 1.2. Центральное проецирование.

Для этого из центра S через точки проведем проецирующие лучи до пересечения с плоскостью проекций. A_p и B_p– проекции точек А и В на плоскость проекций p.

Если для некоторой точки К проецирующий луч оказался параллелен плоскости проекций p, то проекция К_p находится в несобственной точке, т.е. К_p удалена в бесконечность.

Параллельное проецирование

Аппаратом параллельного проецирования является плоскость проекций p и заданное направление проецирования s. Центр проецирования S удален в бесконечность. Сущность способа в том, что все проецирующие лучи параллельны друг другу. Параллельное проецирование является частным случаем центрального проецирования.

Определим параллельные проекции точек A и B (рис. 1.3а).

Для этого через точки параллельно направлению проецирования проведем проецирующие лучи до пересечения с плоскостью p и найдем проекции точек A_p и B_p.

Обратим внимание, что каждой точке пространства соответствует проекция на плоскости. Однако каждой проекции на плоскости соответствует бесконечное множество точек пространства, т.е. проекция точки на плоскость не определяет ее положение в пространстве.

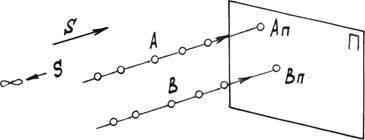
Рис. 1.3а. Параллельное проецирование.

Для однозначного определения точки в пространстве необходимо иметь два направления проецирования s₁ и s₂ (рис. 1.3б). Тогда две проекции на плоскость A₁_p и А₂_p однозначно определяют ее положение в пространстве.

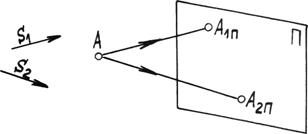
Рис. 1.3б. Параллельное проецирование.