Тонкость помола и зерновая характеристика угольной пыли.

Качество пыли характеризуется тонкостью размола и соотношением фракций. Гранулометрический состав топлива определяют методом ситового анализа. Для этого навеску топлива массой 50-100 г рассеивают на стандартном наборе сит и определяют массу топлива, оставшегося на каждом сите g_i – остаток топлива в диапазоне размеров от d_i до δ_i+1. Полный остаток R_i на сите (масса, выраженная в процентах) является суммой остатка на данном сите и остатков на вышележащих ситах.

С помощью сит возможно рассеивать только пыль с размером зерен более 40 мкм. Анализ фракционного состава более мелкой пыли проводят методом воздушной классификации.

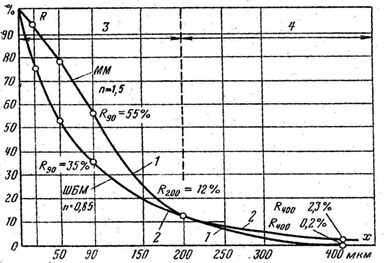
Для наглядности и удобства использования результаты рассева изображают графически в виде зерновой характеристики, где по оси абсцисс отложен размер сита, а по оси ординат полный остаток на сите данного размера. Анализ многочисленных зерновых характеристик размола различных видов топлив показал, что все кривые описываются уравнением Розина-Раммлера (рис. 4.8).

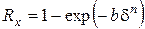, (4.33)

где δ – текущий размер угольной пыли; b и n - постоянные для данного топлива и данного метода размола величины, b –характеризует тонкость измельчения, чем больше b, тем тоньше пыль. Числовые значения для b = 4×10^-3 – для грубой пыли, b = 40×10^-3 – для тонкой, n – коэффициент полидисперсности пыли – характеризует структуру пыли с точки зрения равномерности помола. Чем выше n, тем меньше отличаются своими размерами частицы. Для промышленных условий коэффициент n имеет значение 0,75-1,5.

Уравнение Розина-Раммлера может быть представлено в следующем виде:

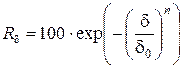, (4.34)

где d₀ - характерный размер частиц в навеске, равный .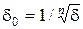

При d = 0 остаток на сите R_δ = 100 %, при d®¥ R_d = 0, т.е. больших частиц мало. По физическому смыслу d₀ – это размер, при котором средняя удельная поверхность частиц размером d₀ равна средней удельной поверхности рассматриваемых полидисперсных частиц.

При наличии экспериментальных данных по остаткам на сите коэффициенты в уравнении Розина-Раммлера находят, дважды логарифмируя выражение (4.34):

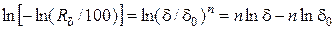(4.35)

и обрабатывая данные в координатах 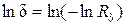, в которых уравнение (4.35) представляет собой уравнение прямой с искомыми величинами n и d₀.