Итак, масса дерева равна

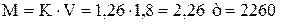кг.

Результирующая сила взаимодействия ЗУ с деревом при подтаскивании равна (при α = 20⁰)

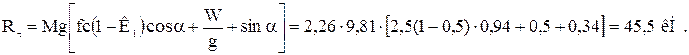Здесь принято:

К₁ – коэффициент, учитывающий распределение массы дерева в захвате и на земле, (@0,5);

f_c – коэффициент сопротивления волочению кроны дерева по земле (в неблагоприятных условиях равен ≈ 2,5);

w – ускорение подтаскивания;

α – угол уклона (равен ≈ 20⁰).

В соответствии с гипотезой взаимодействия ЗУ с деревом принято равномерное распределение усилий в трёх контактных точках.

Поэтому имеем при подтаскивании

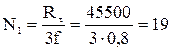кН,

где f – коэффициент трения металла о кору дерева.

Касательную силу F₁ находим из условия проскальзывания конца рычага при обжатии дерева

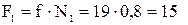кН.

Усилие на штоке гидроцилиндра находим из уравнения равновесия сил

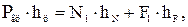
которое решаем относительно Р_гц для каждой конкретной схемы, принятой студентами.

4. Составление расчётной схемы для определения прочности рычага сводится к определению опасного сечения. В качестве расчётного возьмём сечение, в котором изгибающий момент в плоскости вращения рычага имеет максимальное значение. Положение этого сечения определяется точкой пересечения линии действия реакции в шарнире О с нейтральной линией (рис. 1.6). В сечении 1-1 изгибающий момент в плоскости рычага имеет максимальное значение. Кроме этого изгибающего момента, в сечении 1-1 имеет место также поперечный изгибающий момент, равный произведению поперечной силы 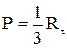на плечо h_p (рис. 1.6).

К двум составляющим изгибающих моментов необходимо добавить крутящий момент

.

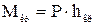Итак, расчетное сечение оказывается нагруженным изгибающим моментом в двух плоскостях, крутящим моментом, нормативными к плоскости сечения силами и двумя составляющими поперечных (касательных) сил.

Само по себе сечение принадлежит к кривому брусу. Поэтому имеем сложное нагружение кривого бруса. Возникает проблема прочности кривого бруса.

5. Анализ нагрузок, действующих на рычаг, проведём в зависимости от проектных параметров β, γ, b. Для этого установим количественную связь между усилием на штоке гидроцилиндра Р_гц и перечисленными проектными параметрами.

Если на размеры (длину) гидроцилиндра ограничений не наложено, то при подтаскивании дерева имеем

*

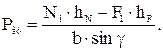Отсюда следует тривиальный вывод: для уменьшения усилий на штоке гидроцилиндра необходимо иметь в момент обжатия дерева максимального диаметра линию действия силы Р_гц перпендикулярно линии ОО_ц, когда угол

γ = 90^о.

Если по соображениям компоновки это сделать не удается, то стремятся так разместить гидроцилиндр, чтобы угол между его продольной осью и линией ОО_ц был бы по возможности близок к 90^о.

Рассмотрим далее более сложную проблему, когда конструктивное пространство для размещения гидроцилиндра ограничено. Пусть h – максимальный допустимый размер по длине гидроцилиндра, а l – ход штока этого гидроцилиндра. Ходу штока l соответствует вполне определённый угол поворота рычага, зависящий от расстояния ОО_ц = b (рис. 1.6, б). С другой стороны угол β определяется рабочим диапазоном поворота рычага от раскрытого положения при захвате дерева максимального диаметра до закрытого положения обжатия дерева минимального диаметра.

* При обжатии ствола
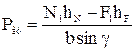
а)		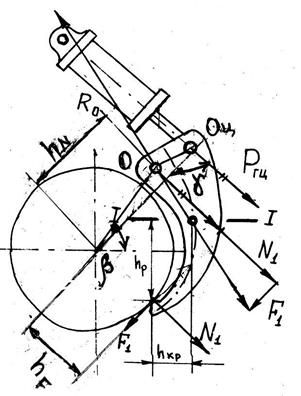б)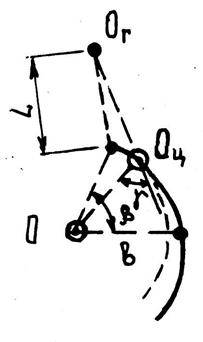
а – расчетная схема; б – кинематическая схема. Рис. 1.6. Расчетная схема сил, приложенных к рычагу ЗУ

Проблема выбора угла β состоит в том, что чем больше β, тем проще наведение и захват дерева. Но при этом требуется больший ход штока, длиннее гидроцилиндр, больше его масса. Для того чтобы вписаться в отводимое конструктивное пространство, необходимо при увеличении угла β уменьшать расстояние ОО_ц = b, что неизбежно влечёт за собой увеличение усилия на штоке гидроцилиндра, увеличение диаметра и массы последнего.

Таким образом, возникает следующая проблема оптимизации:

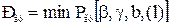, l ≤ l_доп, β ≤ β_доп, γ ? Г.

Можно доказать, что оптимум будет на границе l = l_доп, β =β _доп.

Поиск оптимального решения можно осуществить геометрическими построениями с использованием компоновочно-кинематической схемы, вычерченной в некотором масштабе.

Но можно получить и аналитическое решение, установить аналитические связи между параметрами, показанными на рис. 1.6. Установление последних важно при решении задачи на ЭВМ.

В конце анализа ответим на вопрос: каким образом будет влиять выбор точки 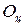на нагрузки в расчетном сечении?

Прежде чем ответить на этот вопрос, рассмотрим случай, когда линия действия силы 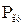параллельна линии равнодействующей 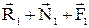. Этот частный случай замечателен тем, что при смещении точки 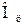сечение 1-1 с максимальным изгибающим моментом в плоскости рычага не изменит своего положения. Но вместе со смещением точки 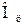будет изменяться нейтральная линия и будет изменяться величина 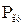. Поэтому сечение точки 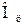приведет к изменению расчетного сечения, а следовательно, и расчетных нагрузок в ней. В итоге возникает более сложная проблема оптимизации, требующая решения задачи

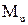= min max 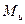( 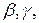b).

Минимум максимального значения изгибающего момента может быть определен с помощью соответствующего алгоритма, реализуемого на ЭВМ.