Статистика электронов и дырок в полупроводниках
Любое твёрдое тело состоит из громадного числа отдельных частиц 1022 – 1023 в кубическом сантиметре. Аналитически описать поведение такого ансамбля частиц просто невозможно из – за невообразимой сложности системы уравнений и колоссального количества этих уравнений. Однако оказалось, что точное описание поведения частицы в таком ансамбле не только невозможно, но и ненужно. Дело в том, что свойства твёрдого тела определяются вероятностными, статистическими параметрами всего ансамбля, а не отдельных его элементов. Это относится к любому большому коллективу частиц, а не только к твёрдому телу – жидкостям, газу, человеческому сообществу, наконец.
Полупроводниковый кристалл можно рассматривать как ансамбль частиц с энергией Wi у каждой частицы. Среднее число частиц системы с энергией от W до W + dW определяется полной статистической функцией распределения N (W) dW, которую можно представить произведением числа состояний g (W) dW, приходящихся на интервал энергий dW на вероятность заполнения этих состояний частицами f (W): N (W) dW = g (W) f (W) dW. f (W) называют функцией распределения – это вероятность заполнения данных состояний. Вероятность заполнения энергетических состояний электронами описывается функцией Ферми - Дирака:
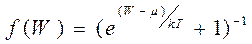 , (2.2)
, (2.2)
где k = 0,86 · 10 – 4 эВ/град - постоянная Больцмана; Т – температура; μ – химический потенциал (энергия Ферми).

 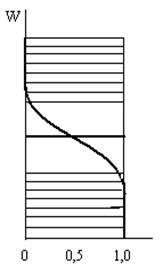
| Энергия Ферми – это энергия некоторого характеристического уровня, относительно которого кривая вероятности симметрична (см.рис. 2.5). При Т = 00 К функция Ферми – Дирака обладает следующими свойствами: f (W) = 1, если W< μ, и f (W) = 0, если W > μ (линия 1 на рис.2.5), т.е. все валентные уровни заполнены, а все уровни зоны проводимости пустые. При повышении температуры происходит термогенерация носителей. Часть валентных электронов переходит в зону проводимости и вероятность заполнения - |
уровней валентной зоны становится меньше единицы (кривая 2 на рис.2.5). При высокой температуре (Т→ ∞) вероятность заполнения любого разрешённого уровня f (W) → 0,5 (прямая 3 на рис.2.5).
Симметричное расположение уровня Ферми подтверждает положение о равенстве числа электронов и дырок в собственном полупроводнике ni = pi.
В примесных полупроводниках кривая распределения смещается либо к зоне проводимости (для донорных полупроводников), либо к валентной зоне (для акцепторных полупроводников). Зонные диаграммы и функции Ферми – Дирака для примесных полупроводников показаны на рис. 2.6. Слева приведена зонная модель и функция вероятности заполнения электронами энергетических уровней для полупроводников n – типа. Уже при комнатной температуре почти все электроны с примесного уровня переходят в зону проводимости. В результате заполнения зоны проводимости электронами примеси кривая распределения, а также уровень Ферми донорных полупроводников μд смещаются вверх.
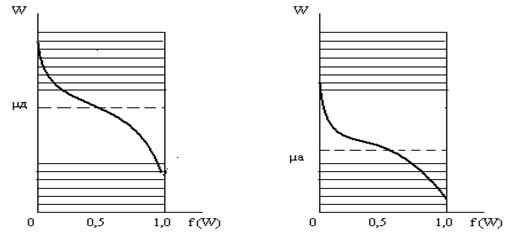
Рисунок 2.6. Кривые распределения вероятностей заполнения энергетических уровней и положение уровня Ферми для n – полупроводников (слева) и р – полупроводников (справа).
Величина этого смещения при данной температуре зависит от концентрации донорной примеси. При значительном повышении концентрации примеси уровень Ферми располагается выше примесного уровня и даже может попасть в зону проводимости.
Для полупроводников р – типа функция Ферми – Дирака и зонная диаграмма показаны на рис.2.6. справа. У этого полупроводника примесный акцепторный уровень расположен на расстоянии Wа от потолка валентной зоны. При комнатной температуре валентные электроны переходят на примесный уровень и в валентной зоне появляется большое количество дырок. В результате кривая распределения и уровень Ферми μа смещаются вниз. Расположение уровня Ферми относительно примесного уровня зависит от концентрации акцепторной примеси (при Т = 00 К уровень располагается ниже примесного, вероятность заполнения которого при этом равна нулю).
Ранее было отмечено, что в примесных полупроводниках существуют основные носители зарядов и неосновные, число которых на несколько порядков меньше, чем основных. При изменении концентрации примесей в полупроводнике изменяется положение уровня Ферми и концентрация носителе зарядов обоих знаков – электронов и дырок. Однако произведение концентраций электронов и дырок в невырожденном полупроводнике (для которого f (W) << 1) при заданной температуре в условиях термодинамического равновесия есть величина постоянная, не зависящая от содержания примесей, т.е.
n 0 p 0 = n i2 . ( 2.3 )
Выражение ( 2.3 ) называют законом действующих масс для носителей зарядов. Оно позволяет всегда найти концентрацию неосновных носителей, если известна концентрация основных носителей заряда.
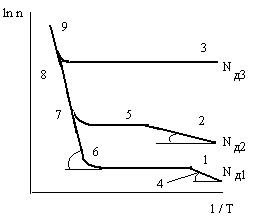
В широком диапазоне температур и для различных концентраций примеси имеют место температурные зависимости концентрации носителей заряда. Такие зависимости для n – полупроводника показаны на рис. 2.7. На этом ри- сунке концентрации (количество в единице объёма) доноров находятся в соотношении: N д 1 < N д 2 < N д 3. При относительно малой концентрации N д1 в области низких температур увеличение концентрации электронов при нагревании полупроводника обусловлено возрастанием степени ионизации доноров (кривая 1, участок 4).
| Каждый ионизованный донор можно рассматривать как центр, захвативший дыр дырку. Учитывая, что общее число энергетических состояний на донорных уровнях равно N д1, для количества ионизованных доноров в полупроводнике запишем:
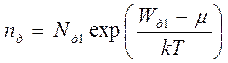 , ( 2.4 ) , ( 2.4 )
|
где Wд1 – положение донорного уровня на энергетической шкале.
При низкой температуре концентрация ионизованных доноров равна концентрации электронов:
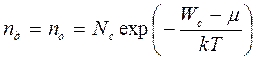 , ( 2.5 )
, ( 2.5 )
где – Wс энергия дна зоны проводимости; 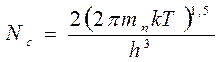
эффективная плотность квантовых состояний в зоне проводимости (h – постоянная Планка; k – постоянная Больцмана; Т – температура, m n - эффективная масса электрона.
Отсюда ( 2.5 ) следует, что
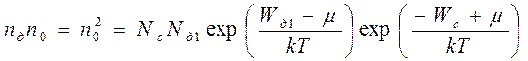
и соответственно
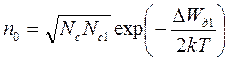 , ( 2.6 )
, ( 2.6 )
где 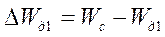 .
.
Из выражения ( 2.6 ) следует, что наклон кривой 1 на участке 4 (рис. 2.7) характеризует энергию ионизации примесей. В процессе дальнейшего нагревания при некоторой температуре, соответствующей излому кривой 1, все электроны примесных уровней перебрасываются в зону проводимости. При этом ионизация собственных атомов полупроводника ещё очень мала. Поэтому в достаточно широком температурном диапазоне концентрация носителей заряда остаётся практически постоянной и равной концентрации доноров (горизонтальный участок кривой 1). Этот участок температурной зависимости называют областью истощения примеси
При относительно высоких (несколько сотен градусов К) температурах начинает преобладать процесс ионизации электронов валентной зоны полупроводника и переброс их в зону проводимости через запрещённую зону, т.е. происходит переход в область собственной проводимости (крутой участок кривой 1 за перегибом 6). Здесь концентрация электронов равна концентрации дырок, а крутизна кривой определяется шириной запрещённой зоны полупроводника.
С увеличением концентрации примеси участки кривых, соответствующие примесной проводимости, смещаются вверх. Кроме того следует принимать во внимание, что с увеличением числа примесных атомов расстояния между ними уменьшается, что приводит к более сильному взаимодействию их электронных оболочек и расщеплению дискретных примесных уровней в зону, Соответственно уменьшается энергия ионизация примесей (угол наклона участков 1 и 2) и повышается температура истощения примесей.
При достаточно большой концентрации доноров ( N д 3 ) их энергия ионизации превращается в ноль, так как образовавшаяся примесная зона перекрывается с зоной проводимости. Такой полупроводник называется вырожденным (почти проводником). Температурная зависимость концентрации носителей заряда в этом случае представляет собой ломанную линию с двумя прямолинейными участками ( кривая 3 – 9 ). Концентрация электронов в вырожденном n – полупроводнике постоянна во всём диапазоне примесной проводимости. Вырожденный полупроводник способен проводить ток при очень низких температура, поэтому иногда его называют «полуметаллом».
Всё сказанное можно отнести и акцепторным, р – полупроводникам с учётом, естественно, особенностей полупроводников с дырочной проводимостью.
В заключение рассмотрим положение уровня Ферми при различной температуре. При низких температурах положение уровня Ферми для невырожденных полупроводников можно определить логарифмируя выражение ( 2.5):
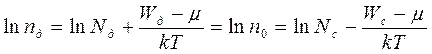 ,
,
отсюда следует, что
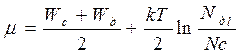 .
.
Как следует из этого выражения при Т = 0 0 К уровень Ферми в полупроводнике n – типа лежит посередине между дном зоны проводимости и примесным (донорным) уровнем (рис. 2.8, слева ), валентная зона и примесный уровень заполнены, зона проводимости пуста, электропроводности нет. При повы -
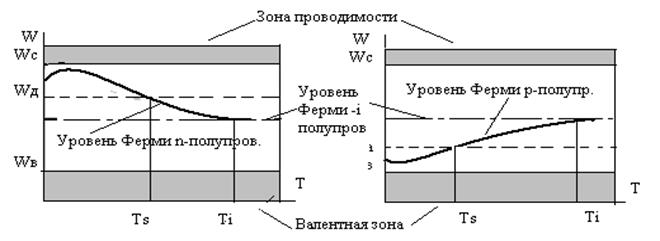
Рисунок 2.8. Зависимость уровня Ферми от температуры для донорных (слева) и акцепторных (справа) полупроводников.
шении температуры начинается ионизация примеси, электроны с примесных уровней перебрасываются в зону проводимости проводимость растёт, уровень Ферми приближается к дну зоны проводимости, достигая максимума. Затем начинает увеличиваться количество электронов в зоне проводимости, ионизованных из валентной зоны – это приводит к снижению уровня Ферми. При температуре Тs все электроны примеси переходят в зону проводимости, т.е. Тs – это температура истощения примеси, она тем выше, чем больше энергия ионизации доноров. Далее всё более заметный вклад в проводимость вносят электроны, перешедшие из валентной зоны, уровень Ферми стремится к середине запрещённой зоны и при температуре Тi – температуре перехода к собственной проводимости, концентрация носителей в собственном полупроводнике совпадает с концентрацией электронов в донорном полупроводнике в области истощения примеси. Тi определяет предельную температуру работы полупроводниковых приборов и она тем выше, чем шире запрещённая зона и выше концентрация примеси ( Тi для германия составляет 480 К, для кремния 650 К ).
Всё сказанное аналогичным образом проявляется и в полупроводниках р – типа, при внесении в собственный полупроводник акцепторной примеси. Как показано на рис. 2.8 справа температурная зависимость уровня Ферми начинается от середины между потолком валентной зоны и примесным акцепторным уровнем при 0 К, проходя через минимум пересекает его при температуре истощения примеси Тs и устанавливается посередине запрещённой зоны при температуре перехода к собственной проводимости Тi .
Здесь уместно ещё раз обратиться к закону действующих масс ( 2.3 ), перефразируя его следующим образом: «Произведение концентраций электронов и дырок в невырожденном полупроводнике не зависит от степени его легирования, а определяется только температурой и равно квадрату концентрации носителей в собственном полупроводнике» - np = ni 2 .
В практике электронного приборостроения используются ещё так называемые компенсированные полупроводники, которые содержат и донорные, и акцепторные примеси и, обладая собственной, электронной или дырочной проводимостями, позволяют расширить диапазон количественных параметров полупроводниковых приборов. Зонные диаграммы компенсированных полупроводников приведены на рис. 2.9.
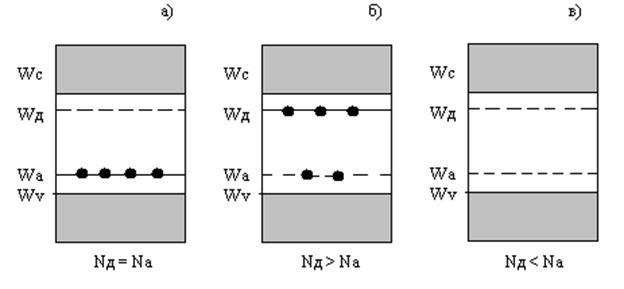
Рисунок 2.9. Компенсированные полупроводники: а) – с собственным характером проводимости; б) - с электронной проводимостью; в) – с дырочной проводимостью.
Полностью компенсированный полупроводник, у которого концентрации донорных и акцепторных примесей равны Nд = Nа (рис. 2.9 –а). При Т → 0 0 К электроны занимают наинизшие уровни, поэтому все акцепторные уровни заполнены, а все донорные – свободны. При повышении температуры электроны переходят в зону проводимости и такой полупроводник обладает собственной проводимостью. Если концентрация доноров превосходит концентрацию акцепторов Nд > Nа (рис. 2.9 –б), то при Т→ 0 0 К все акцепторные уровни заняты. При повышении температуры (Nд - Nа) доноров могут отдавать электроны в зону проводимости, получается аналог электронного полупроводника. Аналогичный механизм присутствует у компенсированных полупроводников с Nд < Nа (рис. 2.9 – в), обладающих дырочной проводимостью из – за разности ( Nа – Nд ). ионизованный донор можно рассматривать как центр, захвативший дырку.
Дата добавления: 2016-11-26; просмотров: 4651;











